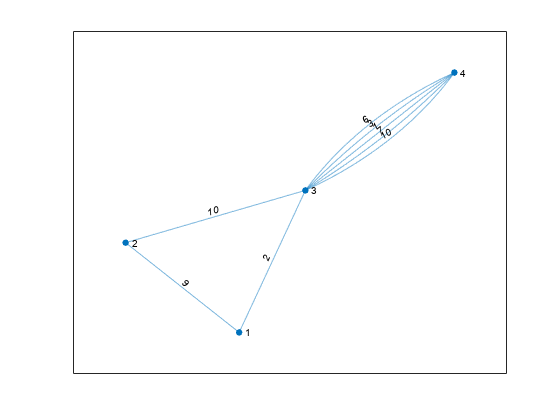
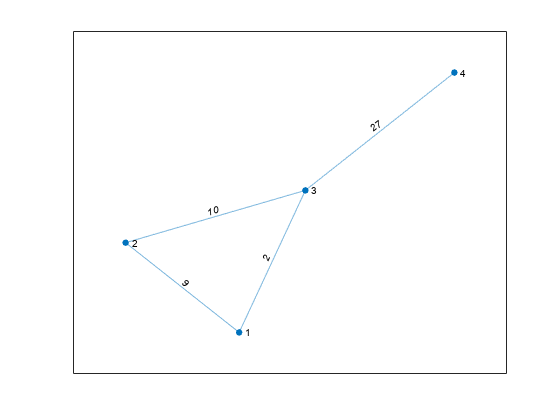
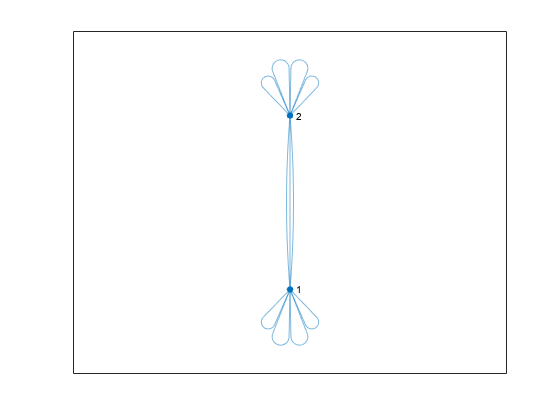
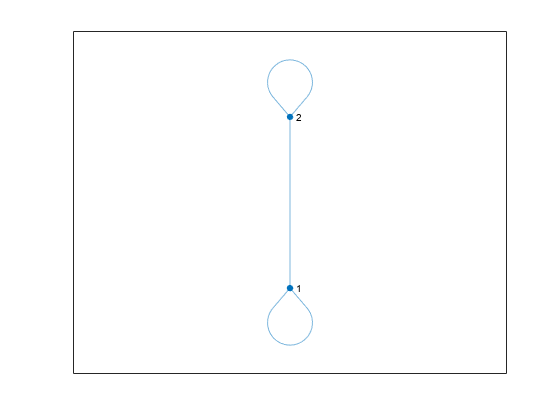
simplify
Reduce multigraph to simple graph
Syntax
Description
H = simplify(G,pickmethod)pickmethod can be 'first' (default),
'last', 'min', or
'max'.
H = simplify(G,aggregatemethod)G are dropped.
aggregatemethod can be 'sum' or
'mean'.
H = simplify(___,selfloopflag)'keepselfloops' specifies that nodes with one or more
self-loops will have one self-loop in the simplified graph.
H = simplify(___,Name,Value)'PickVariable' and a variable in
G.Edges to use that variable with the
'min' or 'max' selection methods.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2018a
See Also
graph | digraph | ismultigraph