bounds
Minimum and maximum values of an array
Syntax
Description
[
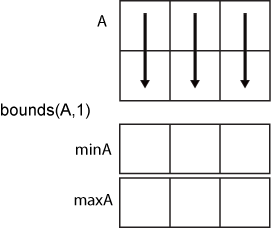
computes the minimum and maximum values based on the dimensions specified in the
vector minA,maxA] = bounds(A,vecdim)vecdim. For example, if A is a matrix,
then bounds(A,[1 2]) returns the minimum and maximum values over
all elements in A, since every element of a matrix is contained
in the array slice defined by dimensions 1 and 2.
[
specifies whether to omit or include missing values in minA,maxA] =
bounds(___,missingflag)A for any
of the previous syntaxes. For example, bounds(A,"missingflag")
includes all missing values when computing the minimum and maximum values. By
default, bounds omits missing values.