accumarray

Accumulate vector elements

Syntax

B = accumarray(ind,data)

B = accumarray(ind,data,sz)

B = accumarray(ind,data,sz,fun)

B = accumarray(ind,data,sz,fun,fillval)

B = accumarray(ind,data,sz,fun,fillval,issparse)

Description

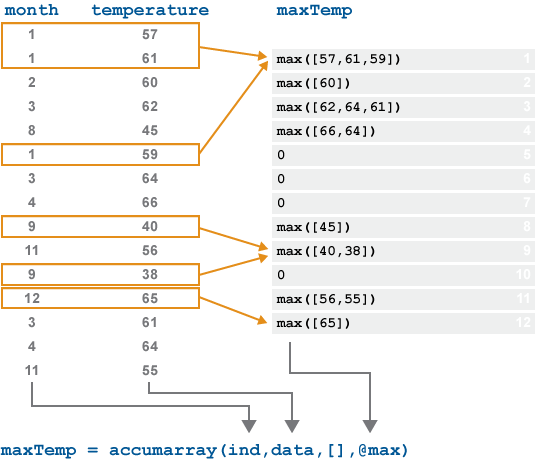
B = accumarray(ind,data) sums groups of data by accumulating elements of a vector data according to the groups specified in ind. The sum is then computed over each group. The values in ind define both the group the data belongs to and the index into the output array B where each group sum is stored.

To return the group sums in order, specify ind as a vector. Then for the group with index i, accumarray returns its sum in B(i). For example, if ind = [1 1 2 2]' and data = [1 2 3 4]', then B = accumarray(ind,data) returns the column vector B = [3 7]'.

To return the group sums in another shape, specify ind as a matrix. For an m-by-n matrix ind, each row represents the group assignment and an n-dimensional index into the output B. For example, if ind contains two rows of the form [3 4], then the sum of the corresponding elements in data is stored in the (3,4) element of B.

Elements of B whose index does not appear in ind are filled with 0 by default.

B = accumarray(ind,data,sz) returns an array B padded to size sz. Specify sz as a vector of positive integers that match or exceed the dimension lengths in ind. Extra elements in the output are filled with 0. Specify sz as [] to let the indices in ind determine the size of the output.

B = accumarray(ind,data,sz,fun) applies the function fun to each group in data specified by ind. Specify fun using the @ symbol, such as @mean, or as [] to use the default @sum.

B = accumarray(ind,data,sz,fun,fillval) fills all elements of B that are not referred to by an index in ind with the scalar value fillval. Specify fillval as [] to use the default value 0.

B = accumarray(ind,data,sz,fun,fillval,issparse) returns an array B that is sparse when issparse is true or 1, and full if issparse is false or 0. The output B is full by default.

Examples

Sum Data by Group

Create a vector of data and a corresponding vector ind that defines groups.

data = (1:6)'

data = 6×1

     1
     2
     3
     4
     5
     6

ind = [1 3 4 2 4 1]'

ind = 6×1

     1
     3
     4
     2
     4
     1

Sum the values in data by the groups specified in ind.

B = accumarray(ind,data)

B = 4×1

     7
     4
     2
     8

Alternatively, use the groupsummary function, specifying 'sum' as the group computation.

B = groupsummary(data,ind,'sum')

B = 4×1

     7
     4
     2
     8

Count Elements in Group

Create a vector of groups.

ind = [1 1 4 2 4 3]';

Apply scalar expansion to the number 1 to count the number of elements in each group defined in ind.

B = accumarray(ind,1)

B = 4×1

     2
     1
     1
     2

Alternatively, use the groupcounts function.

B = groupcounts(ind)

B = 4×1

     2
     1
     1
     2

Specify Output Size

Create a vector of data and a matrix of output indices ind that defines groups of data.

data = 1:6

data = 1×6

     1     2     3     4     5     6

ind = [1 1; 2 2; 3 2; 1 1; 2 2; 4 1]

ind = 6×2

     1     1
     2     2
     3     2
     1     1
     2     2
     4     1

Sum the values in data for each group in ind. The indices in ind define a 4-by-2 matrix of locations for the output.

B1 = accumarray(ind,data)

B1 = 4×2

     5     0
     0     7
     0     3
     6     0

Pad the output to a 4-by-4 matrix by specifying the output size as [4 4].

B2 = accumarray(ind,data,[4 4])

B2 = 4×4

     5     0     0     0
     0     7     0     0
     0     3     0     0
     6     0     0     0

Variance by Group

Calculate group variances rather than sums.

Create a vector of data and a matrix ind that defines groups of the data.

data = [100.1 101.2 103.4 102.8 100.9 101.5]'

data = 6×1

  100.1000
  101.2000
  103.4000
  102.8000
  100.9000
  101.5000

ind = [1 1; 1 1; 2 2; 3 2; 2 2; 3 2]

ind = 6×2

     1     1
     1     1
     2     2
     3     2
     2     2
     3     2

Compute the variance of each group by specifying the function handle @var as the method input. This syntax applies the var function to the groups instead of sum.

B1 = accumarray(ind,data,[],@var)

B1 = 3×2

    0.6050         0
         0    3.1250
         0    0.8450

You can specify the group computation as an anonymous function that accepts vector inputs and returns a scalar. This is useful when you want to pass additional arguments to a function. For example, use the var function with the normalization argument value 1.

A2 = accumarray(ind,data,[],@(x) var(x,1))

A2 = 3×2

    0.3025         0
         0    1.5625
         0    0.4225

Return Sum with Integer Type Output

Specify an additional argument to the sum function by using an anonymous function for the method input.

Create a vector of data and a matrix ind that defines groups of the data and 3-D indices into the output.

data = int8(10:15)

data = 1×6 int8 row vector

   10   11   12   13   14   15

ind = [1 1 1; 1 1 1; 1 1 2; 1 1 2; 2 3 1; 2 3 2]

ind = 6×3

     1     1     1
     1     1     1
     1     1     2
     1     1     2
     2     3     1
     2     3     2

Sum the data by group in their native integer class int8 by using the 'native' option for the sum function. To do this, specify an anonymous function using @(x) sum(x,'native') for the method input. The result is a 2-by-3-by-2 multidimensional array of type int8.

B = accumarray(ind,data,[],@(x) sum(x,'native'))

B = 2×3×2 int8 array
B(:,:,1) =

   21    0    0
    0    0   14


B(:,:,2) =

   25    0    0
    0    0   15

Group Values in Cell Array

Create a vector of data and a matrix ind that defines groups of the data.

data = 1:10

data = 1×10

     1     2     3     4     5     6     7     8     9    10

ind = [1 1; 1 1; 1 1; 1 1; 2 1; 2 1; 2 1; 2 1; 2 1; 2 2]

ind = 10×2

     1     1
     1     1
     1     1
     1     1
     2     1
     2     1
     2     1
     2     1
     2     1
     2     2

Group the elements of data into a cell array.

B = accumarray(ind,data,[],@(x) {x})

B=2×2 cell array
    {4×1 double}    {0×0 double}
    {5×1 double}    {[      10]}

Verify that the vector elements are in the same order as they appear in data.

B{2,1}

ans = 5×1

     5
     6
     7
     8
     9

Specify Fill Value

Create a vector of data and a matrix ind that defines groups of the data.

data = (101:106)'

data = 6×1

   101
   102
   103
   104
   105
   106

ind = [1 1; 2 2; 3 3; 1 1; 2 2; 4 4]

ind = 6×2

     1     1
     2     2
     3     3
     1     1
     2     2
     4     4

The elements of ind define a 4-by-4 matrix for the output, but only reference 4 out of the 16 elements. By default, the other 12 elements are 0 in the output. Fill in the extra output elements with NaN values instead of 0.

B = accumarray(ind,data,[],[],NaN)

B = 4×4

   205   NaN   NaN   NaN
   NaN   207   NaN   NaN
   NaN   NaN   103   NaN
   NaN   NaN   NaN   106

Change Output Sparsity

Create a vector of data and a matrix ind that defines groups of the data.

data = [34 22 19 85 53 77 99 6];
ind = [1 1; 400 400; 80 80; 1 1; 400 400; 400 400; 80 80; 1 1]

ind = 8×2

     1     1
   400   400
    80    80
     1     1
   400   400
   400   400
    80    80
     1     1

The elements of ind define a 400-by-400 matrix for the output, but only reference 3 out of the 160,000 elements. When the output of accumarray results in a large array with a low density of nonzero elements, you can save memory by specifying the issparse option as true, creating a sparse matrix instead of a full one.

B = accumarray(ind,data,[],[],[],true)

B = 400×400 sparse double matrix (3 nonzeros)
   (1,1)      125
  (80,80)     118
 (400,400)    152

Input Arguments

ind — Output indices

vector | matrix | cell array of vectors

Output indices, specified as a vector, matrix, or cell array of vectors.

• If ind is a vector, then each element specifies an index into the output and defines the groups accumulated by accumarray. All of the elements must be positive integers and the length of ind must match the length of the data vector.

• If ind is an m-by-n matrix, then each row specifies an n-dimensional index into the output. The ith row in ind corresponds to the ith value in the data and the number of rows in ind must match the length of the data vector. For example, if ind is a 3-by-2 matrix, it contains three 2-D indices. The first element of each row is the row index into the output and the second element is the column index.

• If ind is a cell array of index vectors, then each vector must have the same length and they are treated as columns.

data — Data to be accumulated

scalar | vector

Data to be accumulated, specified as a scalar or vector.

• If data is a scalar, then its value is scalar expanded.

• If data is a vector, then it must have the same length as the number of rows in the index array.

sz — Size of output array

[] (default) | vector of positive integers

Size of the output array, specified as a vector of positive integers or as []. For example, sz = [5 7] produces an output array that is 5-by-7. When you specify [] for the size, the values in the index array determine the size of the output. The dimension lengths in sz must match or exceed the dimension lengths in the index array.

fun — Group computation

[] (default) | function handle

Group computation, specified as a function handle. accumarray accumulates the elements of the data vector by group, and then applies the function fun to the group elements. When you specify fun = [], the computation uses the default function sum. The specified function must accept a column vector and return a numeric, logical, or char scalar, or a scalar cell. For more information on function handles, see Create Function Handle.

Example: fun = @max

fillval — Fill value

[] (default) | scalar

Fill value when an element of the output does not correspond to an index provided in the index array, specified as a scalar or as [], which uses the default value 0. The data type of fillval must match the data type of the computation function output.

issparse — Output sparsity

false or 0 (default) | true or 1

Output sparsity, specified as a numeric or logical 1 (true) or 0 (false).

When issparse is true or 1, the fill value must be 0 or [], and the input data and output of the computation function must both have type double.

Output Arguments

B — Output array

vector | matrix | multidimensional array

Output array, returned as a vector, matrix, or multidimensional array. B has the same data type as the values returned by the group computation function.

When the size of B is not specified, the output size depends on the index array ind.

• If ind is a column vector, then B is a column vector of length max(ind,[],1).

• If ind is a matrix with more than one column, then B is a multidimensional array of size max(ind,[],1).

More About

Accumulating Elements

The following graphic illustrates the behavior of accumarray on a vector of temperature data taken over a 12-month period. To find the maximum temperature reading for each month, accumarray applies the max function to each group of values in temperature that have identical indices in month.

No values in month point to the 5, 6, 7, or 10 positions of the output. The elements of output maxTemp at those indices are 0 by default.

Tips

• The behavior of accumarray is similar to the functions groupsummary and groupcounts for computing summary statistics by group and counting the number of elements in a group, respectively. For more grouping functionality in MATLAB^®, see Data Preprocessing.

• The behavior of accumarray is also similar to that of the histcounts function.

  • histcounts groups continuous values into a 1-D range using bin edges. accumarray groups data using n-dimensional indices.

  • histcounts can only return bin counts and bin placement. accumarray can apply any function to the data.

  You can mimic the behavior of histcounts using accumarray with data = 1.

• The sparse function also has accumulation behavior similar to that of accumarray.

  • sparse groups data using 2-D indices, whereas accumarray groups data using n-dimensional indices.

  • For elements with identical indices, sparse applies the sum function (for double values) or the any function (for logical values) and returns the scalar result in the output matrix. accumarray sums by default, but can apply any function to the data.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• Unless you provide explicit bounds on the accumarray input values, the code generator may not be able to predetermine the size of the accumarray output. Therefore, variable-size arrays and dynamic memory allocation must be enabled.

• The input arguments cannot contain enumerations.

• The function fun must return a full (nonsparse) scalar.

• When fun returns a scalar 1-by-1 cell array:

  • You must specify a value for fillval. The value you specify must be a scalar 1-by-1 cell array, and the content of the cell must have the same data type that fun returns.

  • The order of accumulated values that fun receives as input may not match the order in MATLAB.

• To predetermine the output type for fun, the code generator may call fun before processing the input arguments of accumarray. As a result, if the execution of fun causes side effects, for instance by modifying a global or persistent variable or printing to output, then the generated code results may differ from MATLAB results.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The accumarray function supports GPU array input with these usage notes and limitations:

• The value of fun must be one of @sum (default), @prod, @min, @max, @any, or @all.

• data and fillval must be full (nonsparse) logical or floating-point (double or single) arrays.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a