miller
Miller Cylindrical Projection
Classification
Cylindrical
Identifier
miller
Graticule
Meridians: Equally spaced straight parallel lines 0.73 as long as the Equator.
Parallels: Unequally spaced straight parallel lines, perpendicular to the meridians. Spacing increases toward the poles, less rapidly than that of the Mercator projection.
Poles: Straight lines equal in length to the Equator.
Symmetry: About any meridian or the Equator.
Features
This is a projection with parallel spacing calculated to maintain a look similar to the Mercator projection while reducing the distortion near the poles and allowing the poles to be displayed. It is not equal-area, equidistant, conformal, or perspective. Scale is true along the Equator and constant between two parallels equidistant from the Equator. There is no distortion near the Equator, and it increases moderately away from the Equator, but it becomes severe at the poles.
The Miller Cylindrical projection is derived from the Mercator projection; parallels are spaced from the Equator by calculating the distance on the Mercator for a parallel at 80% of the true latitude and dividing the result by 0.8. The result is that the two projections are almost identical near the Equator.
Parallels
For cylindrical projections, only one standard parallel is specified. The other standard parallel is the same latitude with the opposite sign. For this projection, the standard parallel is by definition fixed at 0º.
Remarks
This projection was presented by Osborn Maitland Miller of the American Geographical Society in 1942. It is often used in place of the Mercator projection for atlas maps of the world, for which it is somewhat more appropriate.
Mapping Toolbox™ uses a different implementation of the Miller projection for displaying coordinates on
axesm-based maps than for projecting coordinates using theprojfwdorprojinvfunction. These implementations may produce differing results.The implementation of the Miller projection for displaying coordinates on
axesm-based maps is applicable only for coordinates that are referenced to a sphere. The implementation of the Miller projection for projecting coordinates using theprojfwdorprojinvfunction is applicable for coordinates referenced to either a sphere or an ellipsoid.
Example
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('miller', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;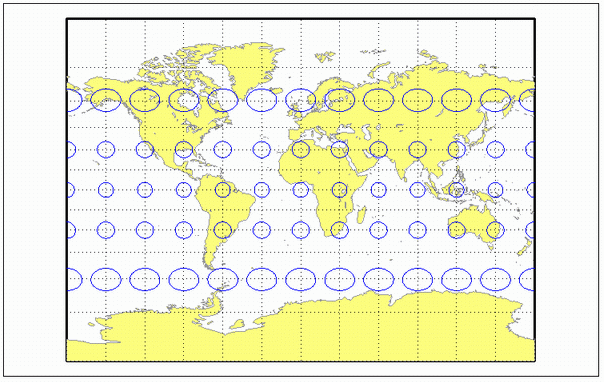
Version History
Introduced before R2006a