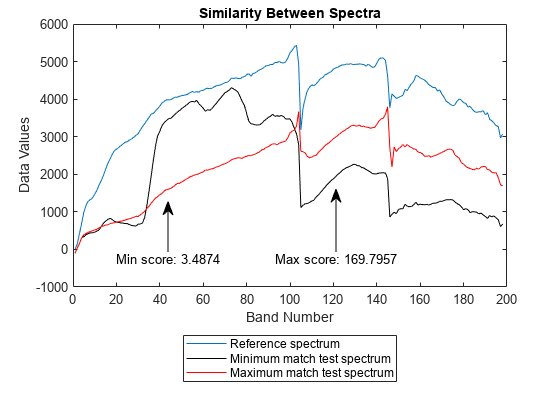
sid
Measure spectral similarity using spectral information divergence
Description
score = sid(inputData,refSpectra)inputData and the specified reference spectra
refSpectra by using the spectral information divergence (SID)
technique. Use this syntax to identify different regions or materials in a hyperspectral
data cube.
score = sid(testSpectra,refSpectra)testSpectra and reference spectra refSpectra by
using the SID method. Use this syntax to compare the spectral signature of an unknown
material against the reference spectra or to compute spectral variability between two
spectral signatures.
Note
This function requires the Hyperspectral Imaging Library for Image Processing Toolbox™. You can install the Hyperspectral Imaging Library for Image Processing Toolbox from Add-On Explorer. For more information about installing add-ons, see Get and Manage Add-Ons.
The Hyperspectral Imaging Library for Image Processing Toolbox requires desktop MATLAB®, as MATLAB Online™ and MATLAB Mobile™ do not support the library.
Examples
Input Arguments
Output Arguments
Limitations
This function does not
support parfor loops, as its performance is already
optimized. (since R2023a)
Algorithms
The sid function normalizes the reference spectra
refSpectra and test spectra testSpectra and
computes the SID value using this formula.
q and p are the vectors of normalized reference and test spectra, respectively. qi and pi are the ith elements of the vectors q and p, respectively. C is the length of vectors q and p.
References
[1] Chein-I Chang. “An Information-Theoretic Approach to Spectral Variability, Similarity, and Discrimination for Hyperspectral Image Analysis.” IEEE Transactions on Information Theory 46, no. 5 (August 2000): 1927–32. https://doi.org/10.1109/18.857802.
Version History
Introduced in R2020a
See Also
spectralMatch | readEcostressSig | sam | hypercube | sidsam