fwind1
2-D FIR filter using 1-D window method
Description
The fwind1 function designs 2-D FIR filters using the
window method. fwind1 uses a 1-D window specification to design a
2-D FIR filter based on the desired frequency response. fwind1 works
with 1-D windows only. Use fwind2 to work with 2-D
windows.
You can apply the 2-D FIR filter to images by using the filter2 function.
Examples
Input Arguments
Output Arguments
Algorithms
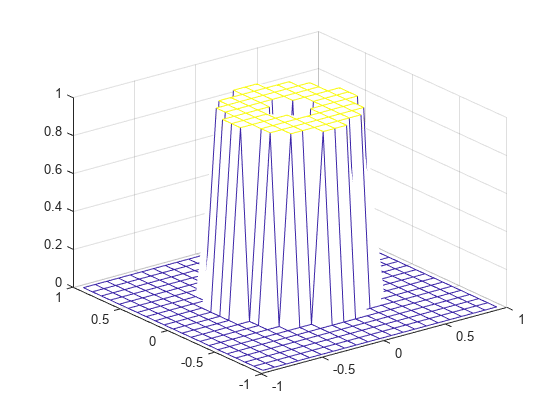
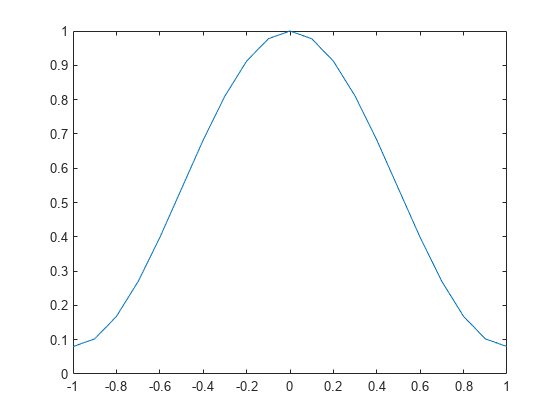
The fwind1 function takes a one-dimensional window specification
and forms an approximately circularly symmetric two-dimensional window using Huang's
method,
where w(t) is the one-dimensional window and w(n1,n2) is the resulting two-dimensional window.
Given two windows, the fwind1 function forms a separable
two-dimensional window:
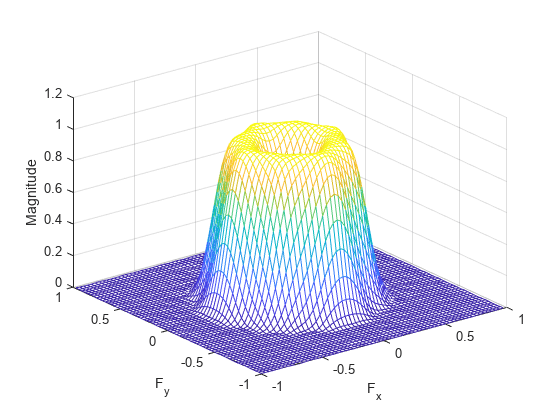
The fwind1 function calls the fwind2 with the desired frequency response Hd and
the two-dimensional window. The fwind2 function calculates
h using an inverse Fourier transform and multiplication by the
two-dimensional window:
References
[1] Lim, Jae S., Two-Dimensional Signal and Image Processing, Englewood Cliffs, NJ, Prentice Hall, 1990.
Version History
Introduced before R2006a