Calculate the Frequency Response of a 2-D Filter
This example shows how to calculate and display the frequency response of a two-dimensional filter using the freqz2 function. The frequency response of a filter describes the gain of a filter at different input frequencies.
With no output arguments, freqz2 creates a mesh plot of the frequency response. For example, consider this FIR filter.
h = [0.1667 0.6667 0.1667
0.6667 -3.3333 0.6667
0.1667 0.6667 0.1667];Calculate and display the 64-by-64 point frequency response of h.
freqz2(h)
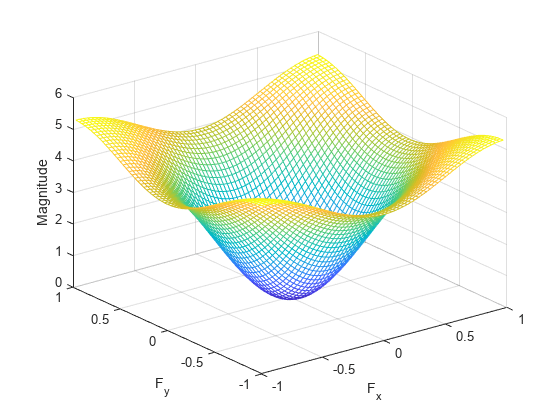
To obtain the frequency response H and the frequency point vectors f1 and f2, use output arguments.
[H,f1,f2] = freqz2(h);
freqz2 normalizes the frequencies f1 and f2 so that the value 1.0 corresponds to half the sampling frequency, or π radians.
For a simple m-by-n response, as shown above, freqz2 uses the two-dimensional fast Fourier transform function fft2. You can also specify vectors of arbitrary frequency points, but in this case freqz2 uses a slower algorithm.
See Also
freqz2 | freqspace | fsamp2 | ftrans2 | fwind1 | fwind2