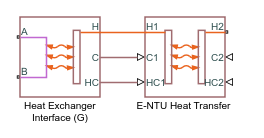
Heat Exchanger (G)

Heat exchanger for systems with gas and controlled flows

• 

Libraries:
Simscape / Fluids / Heat Exchangers / Gas

Description

The Heat Exchanger (G) block models heat exchange between a gas, which flows between ports A1 and B1, and an external, controlled fluid via a physical signal.

Heat Transfer Model

The block heat transfer model derives from the Effectiveness-NTU method. Heat transfer in the steady state then proceeds at a fraction of the ideal rate which the flows, if kept each at its inlet temperature, and if cleared of every thermal resistance in between, could in theory support:

$$Q_{\text{Act}}=ϵQ_{\text{Max}},$$

where Q_Act the actual heat transfer rate, Q_Max is the ideal heat transfer rate, and ε is the fraction of the ideal rate actually observed in a real heat exchanger encumbered with losses. The fraction is the heat exchanger effectiveness, and it is a function of the number of transfer units, or NTU, a measure of the ease with which heat moves between flows, relative to the ease with which the flows absorb that heat:

$$NTU=\frac{1}{R{C}_{\text{Min}}},$$

where the fraction is the overall thermal conductance between the flows and C_Min is the smallest of the heat capacity rates from among the flows that belonging to the flow least capable of absorbing heat. The heat capacity rate of a flow depends on the specific heat of the fluid (c_p) and on its mass flow rate through the exchanger ($$\dot{m}$$):

$$C=c_{\text{p}}\dot{m}.$$

The effectiveness depends also on the relative disposition of the flows, the number of passes between them, and the mixing condition for each. This dependence reflects in the effectiveness expression used, with different flow arrangements corresponding to different expressions. For a list of the effectiveness expressions, see the E-NTU Heat Transfer block.

Flow Arrangement

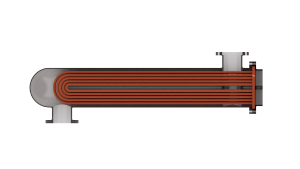
Use the Flow arrangement block parameter to set how the flows meet in the heat exchanger. The flows can run parallel to each other, counter to each other, or across each other. They can also run in a pressurized shell, one through tubes enclosed in the shell, the other around those same tubes. The figure shows an example. The tube flow can make one pass through the shell flow (shown right) or, for greater exchanger effectiveness, multiple passes (left).

Other flow arrangements are possible through a generic parameterization based on tabulated effectiveness data and requiring little detail about the heat exchanger. Flow arrangement, mixing condition, and number of shell or tube passes, if relevant to the heat exchanger, are assumed to manifest in the tabulated data.

Mixing Condition

Use the Cross flow type parameter to mix each of the flows, one of the flows, or none of the flows. Mixing in this context is the lateral movement of fluid in channels that have no internal barriers, normally guides, baffles, fins, or walls. Such movement serves to even out temperature variations in the transverse plane. Mixed flows have variable temperature in the longitudinal plane alone. Unmixed flows have variable temperature in both the transverse and longitudinal planes. The figure shows a mixed flow (i) and an unmixed flow (ii).

The distinction between mixed and unmixed flows is considered only in cross flow arrangements. There, longitudinal temperature variation in one fluid produces transverse temperature variation in the second fluid that mixing can even out. In counter and parallel flow arrangements, longitudinal temperature variation in one fluid produces longitudinal temperature variation in the second fluid and mixing, as it is of little effect here, is ignored.

Effectiveness Curves

Shell-and-tube exchangers with multiple passes (iv.b-e in the figure for 2, 3, and 4 passes) are most effective. Of exchangers with a single pass, those with counter flows (ii are most effective and those with parallel flows (i) are least.

Cross-flow exchangers are intermediate in effectiveness, with mixing condition playing a factor. They are most effective when both flows are unmixed (iii.a) and least effective when both flows are mixed (iii.b). Mixing just the flow with the smallest heat capacity rate (iii.c) lowers the effectiveness more than mixing just the flow with the largest heat capacity rate (iii.d).

Thermal Resistance

The overall thermal resistance, R, is the sum of the local resistances lining the heat transfer path. The local resistances arise from convection at the surfaces of the wall, conduction through the wall, and, if the wall sides are fouled, conduction through the layers of fouling. Expressed in order from the gas side (subscript 1) to the controlled fluid side (subscript 2):

$$R=\frac{1}{U_{\text{1}}{A}_{\text{Th,1}}}+\frac{F_{\text{1}}}{A_{\text{Th,1}}}+R_{\text{W}}+\frac{F_{\text{2}}}{A_{\text{Th,2}}}+\frac{1}{U_{\text{2}}{A}_{\text{Th,2}}},$$

where U is the convective heat transfer coefficient, F is the fouling factor, and A_Th is the heat transfer surface area, each for the flow indicated in the subscript. R_W is the thermal resistance of the wall.

The wall thermal resistance and fouling factors are simple constants obtained from block parameters. The heat transfer coefficients are elaborate functions of fluid properties, flow geometry, and wall friction, and derive from standard empirical correlations between Reynolds, Nusselt, and Prandtl numbers. The correlations depend on flow arrangement and mixing condition, and are detailed for each in the E-NTU Heat Transfer block on which the block model is based.

Composite Structure

The block is a composite component built from simpler blocks. A Heat Exchanger Interface (G) block models the gas flow. Physical signals for the heat capacity rate and heat transfer coefficient, along with a thermal port for temperature, capture the controlled flow. An E-NTU Heat Transfer block models the heat exchanged across the wall between the flows.

Ports

Conserving

A1 — Gas port

gas

Opening for gas to enter and exit its side of the heat exchanger.

B1 — Gas port

gas

Opening for gas to enter and exit its side of the heat exchanger.

H2 — Entrance temperature of controlled fluid 2

thermal

Entrance temperature of controlled fluid 2.

Input

C2 — Heat capacity rate

physical signal

Instantaneous value of the heat capacity rate for the controlled flow.

HC2 — Heat transfer coefficient

physical signal

Instantaneous value of the heat transfer coefficient between the controlled flow and the wall.

Parameters

Common

Flow arrangement — Manner in which the flows align in the heat exchanger

Parallel or counter flow (default) | Shell and tube | Cross flow | Generic - effectiveness table

Manner in which the flows align in the heat exchanger. The flows can run parallel to each other, counter to each other, or across each other. They can also run in a pressurized shell, one through tubes enclosed in the shell, the other around those tubes. Other flow arrangements are possible through a generic parameterization based on tabulated effectiveness data and requiring little detail about the heat exchanger.

Number of shell passes — Number of times the flow traverses the shell before exiting

1 (default) | unitless scalar

Number of times the flow traverses the shell before exiting.

Dependencies

To enable this parameter, set Flow arrangement to Shell and tube.

Cross flow type — Mixing condition in each of the flow channels

Both fluids mixed (default) | Both fluids unmixed | Gas mixed & Controlled Fluid unmixed | Gas unmixed & Controlled Fluid mixed

Mixing condition in each of the flow channels. Mixing in this context is the lateral movement of fluid as it proceeds along its flow channel toward the outlet. The flows remain separate from each other. Unmixed flows are common in channels with plates, baffles, or fins. This setting reflects in the effectiveness of the heat exchanger, with unmixed flows being most effective and mixed flows being least.

Dependencies

To enable this parameter, set Flow arrangement to Shell and tube.

Number of heat transfer units vector, NTU — Number of transfer units at each breakpoint in lookup table for heat exchanger effectiveness

unitless numerical array

Number of transfer units at each breakpoint in the lookup table for the heat exchanger effectiveness number. The table is two-way, with both the number of transfer units and the thermal capacity ratio serving as independent coordinates. The block inter- and extrapolates the breakpoints to obtain the effectiveness at any number of transfer units. Interpolation is the MATLAB linear type and extrapolation is nearest.

The numbers specified must be greater than zero and increase monotonically from left to right. The size of the vector must equal the number of rows in the Effectiveness table parameter. If the table has m rows and n columns, the vector for the number of transfer units must be m elements long.

Dependencies

To enable this parameter, set Flow arrangement to Generic - effectiveness table.

Thermal capacity ratio vector, CR — Thermal capacity ratio at each breakpoint in lookup table for heat exchanger effectiveness

unitless numerical array

Thermal capacity ratio at each breakpoint in lookup table for heat exchanger effectiveness. The table is two-way, with both the number of transfer units and the heat capacity rate ratio serving as independent coordinates. The block inter- and extrapolates the breakpoints to obtain the effectiveness at any thermal capacity ratio. Interpolation is the MATLAB linear type and extrapolation is nearest.

The thermal capacity ratios must be greater than zero and increase monotonically from left to right. The size of the vector must equal the number of columns in the Nusselt number table parameter. If the table has m rows and n columns, the vector for the thermal capacity ratio must be n elements long. The thermal capacity ratio is the fraction of minimum over maximum heat capacity rates.

Dependencies

To enable this parameter, set Flow arrangement to Generic - effectiveness table.

Effectiveness table, E(NTU,CR) — Heat exchanger effectiveness at each breakpoint in lookup table over the number of transfer units and thermal capacity ratio

unitless numerical array

Heat exchanger effectiveness at each breakpoint in its lookup table over the number of transfer units and thermal capacity ratio. The block inter- and extrapolates the breakpoints to obtain the effectiveness at any pair of number of transfer units and thermal capacity ratio. Interpolation is the MATLAB linear type and extrapolation is nearest.

The effectiveness values must be not be negative. They must align from top to bottom in order of increasing number of transfer units and from left to right in order of increasing thermal capacity ratio. The number of rows must equal the size of the Number of heat transfer units vector parameter, and the number of columns must equal the size of the Thermal capacity ratio vector parameter.

Dependencies

To enable this parameter, set Flow arrangement to Generic - effectiveness table.

Wall thermal resistance — Resistance of the wall to heat flow by thermal conduction

1.6e-4 K/W (default) | scalar with units of temperature over power

Resistance of the wall to heat flow by thermal conduction, and the inverse of thermal conductance, or the product of thermal conductivity with the ratio of surface area to length. Wall resistance adds to convective and fouling resistances to determine the overall heat transfer coefficient between the flows.

Gas

Minimum free-flow area — Cross-sectional area of the flow channel at its narrowest point

0.01 m^2 (default) | scalar with units of length squared

Smallest total cross-sectional flow area between inlet and outlet. If the channel is a collection of ducts, tubes, slots, or grooves, the value of this parameter is the sum of the smallest areas at the minimum flow area point. This parameter is the area where the fluid velocity is highest. For example, if the fluid flows perpendicular to a bank of tubes, the value of this parameter is the sum of the gaps between the tubes in one cross-section where the sum of the gaps is smallest is smallest.

Gas volume — Total volume of fluid in the gas flow channel

0.01 m^3 (default) | scalar with units of length squared

Total volume of fluid contained in the gas flow channel.

Hydraulic diameter for pressure loss — Effective diameter of the flow channel at its narrowest point

0.1 m (default) | scalar with units of length

Effective inner diameter of the flow at its narrowest point. For channels not circular in cross section, that diameter is of an imaginary circle equal in area to the flow cross section. Its value is the ratio of the minimum free-flow area to a fourth of its gross perimeter.

If the channel is a collection of ducts, tubes, slots, or grooves, the gross perimeter is the sum of the perimeters in the collection. If the channel is a single pipe or tube and it is circular in cross section, the hydraulic diameter is the same as the true diameter.

Laminar flow upper Reynolds number limit — Start of transition between laminar and turbulent zones

2000 (default) | unitless scalar

Start of transition between laminar and turbulent zones. Above this number, inertial forces take hold and the flow grows progressively turbulent. The default value is characteristic of circular pipes and tubes with smooth surfaces.

Turbulent flow lower Reynolds number limit — End of transition between laminar and turbulent zones

4000 (default) | unitless scalar

End of transition between laminar and turbulent zones. Below this number, viscous forces take hold and the flow grows progressively laminar. The default value is characteristic of circular pipes and tubes with smooth surfaces.

Pressure loss model — Mathematical model for pressure loss by viscous friction

Pressure loss coefficient (default) | Correlation for flow inside tubes | Tabulated data - Darcy friction factor vs. Reynolds number | Tabulated data - Euler number vs. Reynolds number

Mathematical model for pressure loss by viscous friction. This setting determines which expressions to use for calculation and which block parameters to specify as input. See the Heat Exchanger Interface (G) block for the calculations by parameterization.

Pressure loss coefficient — Aggregate loss coefficient for all flow resistances between the ports

0.1 (default) | unitless scalar

Aggregate loss coefficient for all flow resistances in the flow channel including the wall friction responsible for major loss and the local resistances, due to bends, elbows, and other geometry changes, responsible for minor loss.

The loss coefficient is an empirical dimensionless number commonly used to express the pressure loss due to viscous friction. It can be calculated from experimental data or, in some cases, obtained from product data sheets.

Dependencies

To enable this parameter, set Pressure loss model to Pressure loss coefficient.

Length of flow path from inlet to outlet — Distance traveled from port to port

1 m (default) | scalar with units of length

Total distance the flow must travel to reach across the ports. In multi-pass shell-and-tube exchangers, the total distance is the sum over all shell passes. In tube bundles, corrugated plates, and other channels in which the flow is split into parallel branches, it is the distance covered in a single branch. The longer the flow path, the steeper the major pressure loss due to viscous friction at the wall.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes and Tabulated data - Darcy friction factor vs Reynolds number.

Aggregate equivalent length of local resistances — Aggregate minor pressure loss expressed as a length

0.1 m (default) | scalar with units of length

Aggregate minor pressure loss expressed as a length. This length is that which all local resistances, such as elbows, tees, and unions, would add to the flow path if in their place was a simple wall extension. The larger the equivalent length, the steeper the minor pressure loss due to the local resistances.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes.

Internal surface absolute roughness — Mean height of surface protrusions behind wall friction

15e-6 m (default) | scalar with units of length

Mean height of the surface protrusions from which wall friction arises. Higher protrusions mean a rougher wall for more friction and so a steeper pressure loss. Surface roughness features in the Haaland correlation from which the Darcy friction factor derives and on which the pressure loss calculation depends.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes.

Laminar friction constant for Darcy friction factor — Pressure loss correction for flow cross section in laminar flow conditions

64 (default) | unitless scalar

Pressure loss correction for flow cross section in laminar flow conditions. This parameter is commonly referred to as the shape factor. Its ratio to the Reynolds number gives the Darcy friction factor for the pressure loss calculation in the laminar zone. The default value belongs to cylindrical pipes and tubes.

The shape factor derives for certain shapes from the solution of the Navier-Stokes equations. A square duct has a shape factor of 56, a rectangular duct with aspect ratio of 2:1 has a shape factor of 62, and an annular tube has a shape factor of 96, as does a slender conduit between parallel plates.

Dependencies

To enable this parameter, set Pressure loss model to Correlation for flow inside tubes.

Reynolds number vector for Darcy friction factor — Reynolds number at each breakpoint in lookup table for Darcy friction factor

unitless numerical array

Reynolds number at each breakpoint in the lookup table for the Darcy friction factor. The block inter- and extrapolates the breakpoints to obtain the Darcy friction factor at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Reynolds numbers must be greater than zero and increase monotonically from left to right. They can span across laminar, transient, and turbulent zones. Their number must equal the size of the Darcy friction factor vector parameter, with which they are to combine to complete the tabulated breakpoints.

Dependencies

To enable this parameter, set Pressure loss model to Tabulated data - Darcy friction factor vs. Reynolds number.

Darcy friction factor vector — Darcy friction factor at each breakpoint in lookup table over Reynolds number

unitless numerical array

Darcy friction factor at each breakpoint in its lookup table over the Reynolds number. The block inter- and extrapolates the breakpoints to obtain the Darcy friction factor at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Darcy friction factors must not be negative and they must align from left to right in order of increasing Reynolds number. Their number must equal the size of the Reynolds number vector for Darcy friction factor parameter, with which they are to combine to complete the tabulated breakpoints.

Dependencies

To enable this parameter, set Pressure loss model to Tabulated data - Darcy friction factor vs. Reynolds number.

Reynolds number vector for Euler number — Reynolds number at each breakpoint in lookup table for Euler number

unitless numerical array

Reynolds number at each breakpoint in the lookup table for the Euler number. The block inter- and extrapolates the breakpoints to obtain the Euler number at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Reynolds numbers must be greater than zero and increase monotonically from left to right. They can span across laminar, transient, and turbulent zones. Their number must equal the size of the Euler number vector parameter, with which they are to combine to complete the tabulated breakpoints.

Dependencies

To enable this parameter, set Pressure loss model to Tabulated data - Euler number vs. Reynolds number.

Euler number vector — Euler number at each breakpoint in lookup table over Reynolds number

unitless numerical array

Euler number at each breakpoint in its lookup table over the Reynolds number. The block inter- and extrapolates the breakpoints to obtain the Euler number at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Euler numbers must not be negative and they must align from left to right in order of increasing Reynolds number. Their number must equal the size of the Reynolds number vector for Euler number parameter, with which they are to combine to complete the tabulated breakpoints.

Dependencies

To enable this parameter, set Pressure loss model to Tabulated data - Euler number vs. Reynolds number.

Heat transfer coefficient model — Mathematical model for heat transfer between fluid and wall

Constant heat transfer coefficient (default) | Correlation for flow inside tubes | Tabulated data - Colburn factor vs. Reynolds number | Tabulated data - Nusselt number vs. Reynolds number and Prandtl number

Mathematical model for heat transfer between fluid and wall. The choice of model determines which expressions to apply and which parameters to specify for heat transfer calculation. See the E-NTU Heat Transfer block for the calculations by parameterization.

Heat transfer surface area — Effective surface area used in heat transfer between fluid and wall

0.4 m^2 (default) | scalar with units of length squared

Effective surface area used in heat transfer between fluid and wall. The effective surface area is the sum of primary and secondary surface areas, or those of the wall, where it is exposed to fluid, and of the fins, if any are used. Fin surface area is normally scaled by a fin efficiency factor.

Gas-wall heat transfer coefficient — Heat transfer coefficient for convection between fluid and wall

100 W/(K*m^2) (default) | scalar

Heat transfer coefficient for convection between fluid and wall. Resistance due to fouling is captured separately in the Fouling factor parameter.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Constant heat transfer coefficient.

Length of flow path for heat transfer — Characteristic length traversed in heat transfer between fluid and wall

1 m (default) | scalar with units of length

Characteristic length traversed in heat transfer between fluid and wall. This length factors in the calculation of the hydraulic diameter from which the heat transfer coefficient and the Reynolds number, as defined in the tabulated heat transfer parameterizations, derives.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Tabulated data - Colburn factor vs. Reynolds number or Tabulated data - Nusselt number vs. Reynolds number and Prandtl number.

Nusselt number for laminar flow heat transfer — Constant assumed for Nusselt number in laminar flow

3.66 (default) | positive unitless scalar

Constant assumed for Nusselt number in laminar flow. The Nusselt number factors in the calculation of the heat transfer coefficient between fluid and wall, on which the heat transfer rate depends. The default value belongs to cylindrical pipes and tubes.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Correlation for flow inside tubes.

Reynolds number vector for Colburn factor — Values of the Reynolds number at which to specify the Colburn factor data

unitless numerical array

Reynolds number at each breakpoint in the lookup table for the Colburn factor. The block inter- and extrapolates the breakpoints to obtain the Colburn factor at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Reynolds numbers must be greater than zero and increase monotonically from left to right. They can span across laminar, transient, and turbulent zones. Their number must equal the size of the Colburn factor vector parameter, with which they are to combine to complete the tabulated breakpoints.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Tabulated data - Colburn factor vs. Reynolds number.

Colburn factor vector — Colburn factor at each breakpoint in lookup table over Reynolds number

unitless numerical array

Colburn factor at each breakpoint in its lookup table over the Reynolds number. The block inter- and extrapolates the breakpoints to obtain the Euler number at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Colburn factors must not be negative and they must align from left to right in order of increasing Reynolds number. Their number must equal the size of the Reynolds number vector for Colburn factor parameter, with which they are to combine to complete the tabulated breakpoints.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Tabulated data - Colburn factor vs. Reynolds number.

Reynolds number vector for Nusselt number — Reynolds number at each breakpoint in lookup table for Nusselt number

unitless numerical array

Reynolds number at each breakpoint in the lookup table for the Nusselt number. The table is two-way, with both Reynolds and Prandtl numbers serving as independent coordinates. The block inter- and extrapolates the breakpoints to obtain the Nusselt number at any Reynolds number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Reynolds numbers must be greater than zero and increase monotonically from left to right. They can span across laminar, transient, and turbulent zones. The size of the vector must equal the number of rows in the Nusselt number table parameter. If the table has m rows and n columns, the Reynolds number vector must be m elements long.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Tabulated data - Nusselt number vs. Reynolds number and Prandtl number.

Prandtl number vector for Nusselt number — Prandtl number at each breakpoint in lookup table for Nusselt number

unitless numerical array

Prandtl number at each breakpoint in the lookup table for the Nusselt number. The table is two-way, with both Reynolds and Prandtl numbers serving as independent coordinates. The block inter- and extrapolates the breakpoints to obtain the Nusselt number at any Prandtl number. Interpolation is the MATLAB linear type and extrapolation is nearest.

The Prandtl numbers must be greater than zero and increase monotonically from left to right. They can span across laminar, transient, and turbulent zones. The size of the vector must equal the number of columns in the Nusselt number table parameter. If the table has m rows and n columns, the Prandtl number vector must be n elements long.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Tabulated data - Nusselt number vs. Reynolds number and Prandtl number.

Nusselt number table, Nu (Re,Pr) — Nusselt number at each breakpoint in lookup table over Reynolds and Prandtl numbers

unitless numerical array

Nusselt number at each breakpoint in its lookup table over the Reynolds and Prandtl numbers. The block inter- and extrapolates the breakpoints to obtain the Nusselt number at any pair of Reynolds and Prandtl numbers. Interpolation is the MATLAB linear type and extrapolation is nearest. By determining the Nusselt number, the table feeds the calculation from which the heat transfer coefficient between fluid and wall derives.

The Nusselt numbers must be greater than zero. They must align from top to bottom in order of increasing Reynolds number and from left to right in order of increasing Prandtl numbers. The number of rows must equal the size of the Reynolds number vector for Nusselt number parameter, and the number of columns must equal the size of the Prandtl number vector for Nusselt number parameter.

Dependencies

To enable this parameter, set Heat transfer coefficient model to Tabulated data - Nusselt number vs. Reynolds number and Prandtl number.

Fouling factor — Measure of thermal resistance due to fouling deposits

1.6e-4 K/W (default) | scalar with units of temperature over power

Measure of thermal resistance due to fouling deposits which over time tend to build on the exposed surfaces of the wall. The deposits, as they impose between the fluid and wall a new solid layer through which heat must traverse, add to the heat transfer path an extra thermal resistance. Fouling deposits grow slowly and the resistance due to them is accordingly assumed constant during simulation.

Minimum fluid-wall heat transfer coefficient — Lower bound for the heat transfer coefficient

100 W/(m^2 * K) (default) | scalar with units of power/area/temperature

Lower bound for the heat transfer coefficient between fluid and wall. If calculation returns a lower heat transfer coefficient, this bound replaces the calculated value.

Controlled Fluid

Heat transfer surface area — Aggregate heat transfer surface area on the controlled fluid side

0.4 m^2 (default) | scalar with units of length squared

Aggregate heat transfer surface area on the controlled fluid side

Fouling factor — Measure of thermal resistance due to fouling deposits

1e-4 K/W (default) | scalar with units of length squared times temperature over power

Measure of thermal resistance due to fouling deposits which over time tend to build on the exposed surfaces of the wall. The deposits, as they impose between the controlled fluid and wall a new solid layer through which heat must traverse, add to the heat transfer path an extra thermal resistance. Fouling deposits grow slowly and the resistance due to them is accordingly assumed constant during simulation.

Minimum fluid-wall heat transfer coefficient — Lower bound for the heat transfer coefficient

100 W/(m^2 * K) (default) | scalar with units of power/area/temperature

Lower bound for the heat transfer coefficient between the controlled fluid and wall. If calculation returns a lower heat transfer coefficient, this bound replaces the calculated value.

Effects and Initial Conditions

Gas initial temperature — Temperature in the gas channel at the start of simulation

293.15 K (default) | scalar with units of temperature

Temperature in the gas channel at the start of simulation.

Gas initial pressure — Pressure in the gas channel at the start of simulation

0.101325 MPa (default) | scalar with units of pressure

Pressure in the gas channel at the start of simulation.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2017b

R2024a: Heat Exchanger (G) block only models E-NTU modeling option

The Modeling option parameter has been removed, and the modeling options are now two separate blocks. The Heat Exchanger (G) block uses the heat transfer model that was previously used when Modeling option was E-NTU Model. To use the block model used when Modeling option was Simple model, see the Specific Dissipation Heat Exchanger (G) block.