Specific Dissipation Heat Transfer
Simple heat transfer model between two general fluids
Libraries:
Simscape /
Fluids /
Heat Exchangers /
Fundamental Components
Description
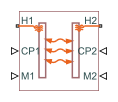
The Specific Dissipation Heat Transfer block models the heat transfer between two fluids given only minimal knowledge of component parameters. The fluids are controlled by physical signals, with these providing the entrance mass flow rate and isobaric specific heat for each. Thermal ports set the entrance temperatures of the fluids.
The rate of heat transfer is calculated from the specific dissipation, a parameter specified in tabulated form as a function of the entrance mass flow rates. The specific dissipation quantifies the amount of heat exchanged between the fluids per unit of time when the entrance temperatures differ by one degree.
This block does not model pressure losses and other aspects of flow mechanics. These effects are captured by the heat exchanger interface blocks. Combine this block with either the Specific Dissipation Heat Exchanger Interface (G) or Specific Dissipation Heat Exchanger Interface (TL) blocks to model a heat exchanger.
Heat Transfer Rate
Heat flows from the warmer fluid to the cooler fluid, at a rate proportional to the difference between the fluid entrance temperatures. The heat flow rate is positive if fluid 1 enters at a higher temperature than fluid 2 and therefore if heat flows from fluid 1 to fluid 2:
where T*,in are the fluid entrance temperatures, determined by the conditions at thermal port H1 for fluid 1 and H2 for fluid 2. ξ is the specific dissipation obtained from the specified tabulated data at the given mass flow rates:
where are the entrance mass flow rates, specified through physical signal port M1 for fluid 1 and M2 for fluid 2.
The specific dissipation is the heat exchanger heat transfer rate divided by the difference in inlet temperatures
The specific dissipation is also equal to the overall heat transfer coefficient defined based on inlet temperature multiplied by the heat transfer surface area or the heat capacity rate multiplied by the effectiveness factor, for whichever fluid has a smaller value.
The heat transfer rate is constrained so that the specific dissipation used in the calculations can never exceed the maximum value:
where C* are the thermal capacity rates of the controlled fluids, each defined as:
with cp,* denoting the isobaric specific heat of the fluid, specified through physical signal port CP1 for fluid 1 and CP2 for fluid 2. The constraint on the maximum heat transfer rate is implemented in the form of a piecewise function:
The block issues a warning whenever the heat flow rate
exceeds the maximum value, if the Check if violating maximum specific
dissipation parameter is
Warning.
Ports
Input
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2017b