Solve Feasibility Problem

Some problems require you to find a point that satisfies all constraints, with no objective function to minimize. For example, suppose that you have the following constraints:

$$\begin{array}{l}(y+x^2{)}^2+0.1y^2\le 1\\ y\le \exp (-x)-3\\ y\le x-4.\end{array}$$

Do any points $$(x,y)$$ satisfy the constraints? To find out, write a function that returns the constraints in a structure field Ineq. Write the constraints in terms of a two-element vector $$x=(x_1,x_2)$$ instead of $$(x,y)$$. Write each inequality as a function $$c(x)$$, meaning the inequalities $$c(x)\le 0$$, by subtracting the right side of each inequality from both sides. To enable plotting, write the function in a vectorized manner, where each row represents one point. The code for this helper function, named objconstr, appears at the end of this example.

Plot the points where the three functions satisfy equalities for $$-2\le x\le 2$$ and $$-4\le y\le 2$$, and indicate the inequalities by plotting level lines for function values equal to –1/2.

[XX,YY] = meshgrid(-2:0.1:2,-4:0.1:2);
ZZ = objconstr([XX(:),YY(:)]).Ineq;
ZZ = reshape(ZZ,[size(XX),3]);
h = figure;
ax = gca;
contour(ax,XX,YY,ZZ(:,:,1),[-1/2 0],'r','ShowText','on');
hold on
contour(ax,XX,YY,ZZ(:,:,2),[-1/2 0],'k','ShowText','on');
contour(ax,XX,YY,ZZ(:,:,3),[-1/2 0],'b','ShowText','on');
hold off

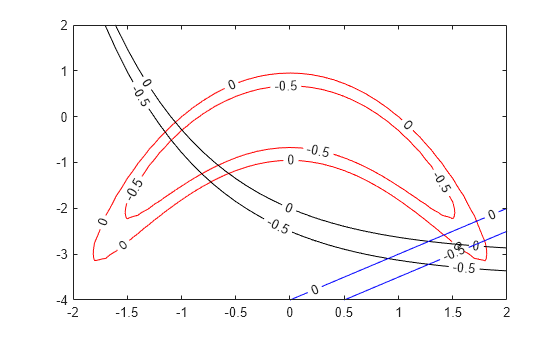
The plot shows that feasible points exist near [1.75,–3].

Set lower bounds of –5 and upper bounds of 3, and solve the problem using surrogateopt.

rng(1) % For reproducibility
lb = [-5,-5];
ub = [3,3];
[x,fval,exitflag,output,trials] = surrogateopt(@objconstr,lb,ub)

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

x = 1×2

    1.7553   -3.0551

fval =

  1x0 empty double row vector

exitflag = 
0

output = struct with fields:
        elapsedtime: 19.3875
          funccount: 200
    constrviolation: -0.0660
               ineq: [-0.0660 -0.2280 -0.8104]
           rngstate: [1x1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ...'

trials = struct with fields:
       X: [200x2 double]
    Ineq: [200x3 double]

Check the feasibility at the returned solution x.

disp(output.ineq)

   -0.0660   -0.2280   -0.8104

Equivalently, evaluate the function objconstr at the returned solution x.

disp(objconstr(x).Ineq)

   -0.0660   -0.2280   -0.8104

Equivalently, examine the Ineq field in the trials structure for the solution x. First, find the index of x in the trials.X field.

indx = ismember(trials.X,x,'rows');
disp(trials.Ineq(indx,:))

   -0.0660   -0.2280   -0.8104

All constraint function values are negative, indicating that the point x is feasible.

View the feasible points evaluated by surrogateopt.

opts = optimoptions("surrogateopt");
indx = max(trials.Ineq,[],2) <= opts.ConstraintTolerance; % Indices of feasible points
figure(h);
hold on
plot(trials.X(indx,1),trials.X(indx,2),'*')
xlim([1 2])
ylim([-3.5 -2.5])
hold off

This code creates the objconstr helper function.

function f = objconstr(x)
c(:,1) = (x(:,2) + x(:,1).^2).^2 + 0.1*x(:,2).^2 - 1;
c(:,2) = x(:,2) - exp(-x(:,1)) + 3;
c(:,3) = x(:,2) - x(:,1) + 4;
f.Ineq = c;
end