retroCorrect
Description
The retroCorrect function corrects the state estimate and
covariance using an out-of-sequence measurement (OOSM). To use this function, specify the
MaxNumOOSMSteps property of the filter as a positive integer. Before
using this function, you must use the retrodict
function to successfully retrodict the current state to the time at which the OOSM was
taken.
[
corrects the filter with the OOSM measurement retroCorrState,retroCorrCov] = retroCorrect(filter,z)z and returns the
corrected state and state covariance. The function changes the values of
State and StateCovariance properties of the
filter object to retroCorrState and retroCorrCov,
respectively. If the filter is a trackingIMM
object, the function also changes the ModelProbabilities property of
the filter.
___ = retroCorrect(___,
specifies the measurement parameters for the measurement measparams)z.
Caution
You can use this syntax only when the specified filter is a
trackingEKF or trackingIMM
object.
Examples
Generate a truth trajectory using the 3-D constant velocity model.
rng(2021) % For repeatable results initialState = [1; 0.4; 2; 0.3; 1; -0.2]; % [x; vx; y; vy; z; vz] dt = 1; % Time step steps = 10; sigmaQ = 0.2; % Standard deviation for process noise states = NaN(6,steps); states(:,1) = initialState; for ii = 2:steps w = sigmaQ*randn(3,1); states(:,ii) = constvel(states(:,ii-1),w,dt); end
Generate position measurements from the truths.
positionSelector = [1 0 0 0 0 0; 0 0 1 0 0 0; 0 0 0 0 1 0];
sigmaR = 0.2; % Standard deviation for measurement noise
positions = positionSelector*states;
measures = positions + sigmaR*randn(3,steps); Show the truths and measurements in an x-y plot.
figure plot(positions(1,:),positions(2,:),"ro","DisplayName","Truths"); hold on; plot(measures(1,:),measures(2,:),"bx","DisplayName","Measures"); xlabel("x (m)") ylabel("y (m)") legend("Location","northwest")
Assume that, at the ninth step, the measurement is delayed and therefore unavailable.
delayedMeasure = measures(:,9); measures(:,9) = NaN;
Construct an extended Kalman filter (EKF) based on the constant velocity model.
estimates = NaN(6,steps); covariances = NaN(6,6,steps); estimates(:,1) = positionSelector'*measures(:,1); covariances(:,:,1) = 1*eye(6); filter = trackingEKF(@constvel,@cvmeas, ... "State",estimates(:,1),... "StateCovariance",covariances(:,:,1), ... "HasAdditiveProcessNoise",false, ... "ProcessNoise",eye(3), ... "MeasurementNoise",sigmaR^2*eye(3), ... "MaxNumOOSMSteps",3);
Step through the EKF with the measurements.
for ii = 2:steps predict(filter); if ~any(isnan(measures(:,ii))) % Skip if unavailable correct(filter,measures(:,ii)); end estimates(:,ii) = filter.State; covariances(:,:,ii) = filter.StateCovariance; end
Show the estimated results.
plot(estimates(1,:),estimates(3,:),"gd","DisplayName","Estimates");
Retrodict to the ninth step, and correct the current estimates by using the out-of-sequence measurements at the ninth step.
[retroState,retroCov] = retrodict(filter,-1); [retroCorrState,retroCorrCov] = retroCorrect(filter,delayedMeasure);
Plot the retrodicted state for the ninth step.
plot([retroState(1);retroCorrState(1)],... [retroState(3),retroCorrState(3)],... "kd","DisplayName","Retrodicted")
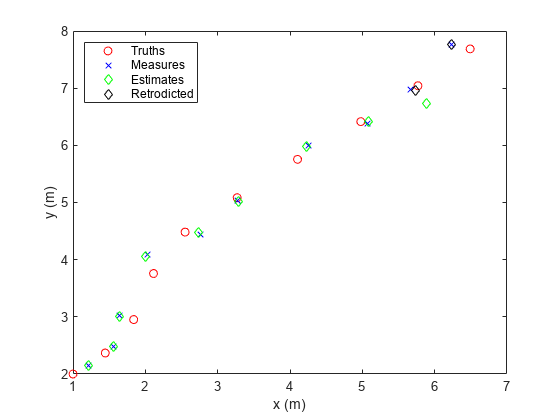
You can use the determinant of the final state covariance to see the improvements made by retrodiction. A smaller covariance determinant indicates improved state estimates.
detWithoutRetrodiciton = det(covariances(:,:,end))
detWithoutRetrodiciton = 8.5281e-06
detWithRetrodiciton = det(retroCorrCov)
detWithRetrodiciton = 7.9590e-06
Consider a target moving with a constant velocity model. The initial position is at [100; 0 ;1] in meters. The velocity is [1; 1; 0] in meters per second.
rng(2022) % For repeatable results
initialPosition = [100; 0; 1];
velocity = [1; 1; 0];Assume the measurement noise covariance matrix is
measureCovaraince = diag([1; 1; 0.1]);
Generate a measurement every second for a duration of five seconds.
measurements = NaN(3,5); dt = 1; for i =1:5 measurements(:,i) = initialPosition + i*dt*velocity + sqrt(measureCovaraince)*randn(3,1); end
Assume the measurement at the fourth second is out-of-sequence. It only becomes available after the fifth second.
oosm = measurements(:,4); measurements(:,4) = NaN;
Create a trackingIMM filter with the true initial position using the initekfimm function. Set the maximum number of OOSM steps to five.
detection = objectDetection(0,initialPosition); imm = initekfimm(detection); imm.MaxNumOOSMSteps = 5;
Update the filter with the available measurements.
for i = 1:5 predict(imm,dt); if ~isnan(measurements(:,i)) correct(imm,measurements(:,i)); end end
Display the current state, diagonal of state covariance, and model probabilities.
disp("===============Before Retrodiction===============")===============Before Retrodiction===============
disp("Current state:" + newline + num2str(imm.State'))Current state: 106.7626 1.56623 6.15405 1.233862 1.000669 -0.1441939
disp("Diagonal elements of state covariance:" + newline + num2str(diag(imm.StateCovariance)'))Diagonal elements of state covariance: 0.91884 1.1404 0.91861 1.2097 0.91569 1.1156
disp("Model probabities:" + newline + num2str(imm.ModelProbabilities'))Model probabities: 0.51519 0.0016296 0.48318
Retrodict the filter and retrocorrect the filter with the OOSM.
[retroState, retroCov] = retrodict(imm,-1); retroCorrect(imm,oosm);
Display the results after retrodiction. From the results, the magnitude of state covariance is reduced after the OOSM is applied, showing that retrodiction using OOSM can improve the estimates.
disp("===============After Retrodiction===============")===============After Retrodiction===============
disp("Current state:" + newline + num2str(imm.State'))Current state: 106.6937 1.621093 6.124384 1.261032 1.117407 -0.2363415
disp("Diagonal elements of state covariance:" + newline + num2str(diag(imm.StateCovariance)'))Diagonal elements of state covariance: 0.80678 1.0429 0.81196 1.0962 0.80353 1.0231
disp("Model probabities:" + newline + num2str(imm.ModelProbabilities'))Model probabities: 0.5191 0.00034574 0.48055
Input Arguments
Tracking filter object, specified as a trackingKF, trackingEKF, or trackingIMM
object.
Out-of-sequence measurement, specified as a P-by-1 real-valued vector, where P is the size of the measurement.
Measurement parameters, specified as a structure or an array of structures. The
structure is passed into the measurement function specified by the
MeasurementFcn property of the tracking filter. The structure can
optionally contain these fields:
| Field | Description |
Frame | Enumerated type indicating the frame used to report measurements. When detections are
reported using a rectangular coordinate system, set |
OriginPosition | Position offset of the origin of the child frame relative to the parent frame, represented as a 3-by-1 vector. |
OriginVelocity | Velocity offset of the origin of the child frame relative to the parent frame, represented as a 3-by-1 vector. |
Orientation | Frame orientation, specified as a 3-by-3 real-valued orthonormal frame rotation matrix.
The direction of the rotation depends on the
|
IsParentToChild | A logical scalar indicating whether |
HasElevation | A logical scalar indicating if the measurement includes elevation. For measurements
reported in a rectangular frame, if |
HasAzimuth | A logical scalar indicating if the measurement includes azimuth. |
HasRange | A logical scalar indicating if the measurement includes range. |
HasVelocity | A logical scalar indicating if the reported detections include velocity measurements.
For measurements reported in a rectangular frame, if
|
Output Arguments
State corrected by retrodiction, returned as an M-by-1 real-valued vector, where M is the size of the filter state.
State covariance corrected by retrodiction, returned as an M-by-M real-valued positive-definite matrix.
More About
Assume the current time step of the filter is k. At time k, the posteriori state and state covariance of the filter are x(k|k) and P(k|k), respectively. An out-of-sequence measurement (OOSM) taken at time τ now arrives at time k. Find l such that τ is a time step between these two consecutive time steps:
where l is a positive integer and l < k.
In the retrodiction step, the current state and state covariance at time k are predicted back to the time of the OOSM. You can obtain the retrodicted state by propagating the state transition function backward in time. For a linear state transition function, the retrodicted state is expressed as:
where F(τ,k) is the backward state transition matrix from time step k to time step τ. The retrodicted covariance is obtained as:
where Q(k,τ) is the covariance matrix for the process noise and,
Here, P(k|k-l) is the priori state covariance at time k, predicted from the covariance information at time k–l, and
In the second step, retro-correction, the current state and state covariance are corrected using the OOSM. The corrected state is obtained as:
where z(τ) is the OOSM at time τ and W(k,τ), the filter gain, is expressed as:
You can obtain the equivalent measurement at time τ based on the state estimate at the time k, z(τ|k), as
In these expressions, R(τ) is the measurement covariance matrix for the OOSM and:
where H(τ) is the measurement Jacobian matrix.
The corrected covariance is obtained as:
where
For interactive multiple model (IMM) filter (trackingIMM), each member-filter is retrodicted to the time of OOSM in the
same way as the process described above. Also, after obtaining the retrodicted state and
measurement, each member-filter retro-corrects the current state of the filter as above.
Compared with a regular filter, an IMM filter needs to maintain the probability of each member-filter. In the retrodiction step, the probability of each model is first retrodicted using the probability transition matrix. Based on the OOSM, the filter can obtain the likelihood of each member-filter using the retrodicted state, filter probability, and measurement. Then, using the likelihood of each filter, the transition probability matrix, and the model probability at the current time, the filter obtains the updated model probability of each filter at the current time k. For more details, see [2].
References
[1] Bar-Shalom, Y., Huimin Chen, and M. Mallick. “One-Step Solution for the Multistep out-of-Sequence-Measurement Problem in Tracking.” IEEE Transactions on Aerospace and Electronic Systems 40, no. 1 (January 2004): 27–37.
[2] Bar-shalom, Y. and Huimin Chen. “IMM Estimator with Out-of-Sequence Measurements.” IEEE Transactions on Aerospace and Electronic Systems, vol. 41, no. 1, Jan. 2005, pp. 90–98.
Extended Capabilities
In code generation, after calling the filter, you cannot change its
MaxNumOOSMSteps property.
Version History
Introduced in R2021b
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)