solutionfromID
Class: FunctionApproximation.LUTSolution
Namespace: FunctionApproximation
Access a solution found during the approximation process
Syntax
other_solution = solutionfromID(solution,id)
Description
other_solution = solutionfromID(solution,id)FunctionApproximation.LUTSolution object, solution,
with the ID specified by id.
Input Arguments
The solution object containing the solution you want to explore, specified
as a FunctionApproximation.LUTSolution object.
ID of the solution that you want to explore, specified as a scalar integer.
Data Types: double
Output Arguments
FunctionApproximation.LUTSolution object associated
with the specified ID.
Examples
This example shows how to use the solutionfromID method of the FunctionApproximation.LUTSolution object to examine other approximation solutions.
Create a FunctionApproximation.Problem object defining a math function to approximate. Then use the solve method to get a FunctionApproximation.LUTSolution object.
problem = FunctionApproximation.Problem('sin')problem =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: @(x)sin(x)
NumberOfInputs: 1
InputTypes: "numerictype(0,16,13)"
InputLowerBounds: 0
InputUpperBounds: 6.2832
OutputType: "numerictype(1,16,14)"
Options: [1×1 FunctionApproximation.Options]
solution = solve(problem)
Searching for fixed-point solutions. | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 0 | 64 | 0 | 2 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.000000e+00 | | 1 | 784 | 1 | 47 | 16 | 16 | EvenSpacing | 7.812500e-03, 5.388912e-03 | | 2 | 768 | 1 | 46 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.534419e-03 | | 3 | 608 | 1 | 36 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.089765e-03 | | 4 | 592 | 1 | 35 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.272461e-03 | | 5 | 416 | 1 | 24 | 16 | 16 | EvenSpacing | 7.812500e-03, 6.201693e-03 | | 6 | 400 | 1 | 23 | 16 | 16 | EvenSpacing | 7.812500e-03, 6.958889e-03 | | 7 | 224 | 0 | 12 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.013411e-02 | | 8 | 304 | 0 | 17 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.887217e-02 | | 9 | 352 | 1 | 20 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.807773e-03 | | 10 | 320 | 0 | 18 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.695679e-02 | | 11 | 336 | 1 | 19 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.810061e-03 | | 12 | 64 | 0 | 2 | 16 | 16 | EvenPow2Spacing | 7.812500e-03, 1.315166e+00 | | 13 | 576 | 1 | 18 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.803448e-03 | | 14 | 512 | 0 | 16 | 16 | 16 | ExplicitValues | 7.812500e-03, 1.190175e-02 | | 15 | 576 | 1 | 18 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.803448e-03 | Best Solution | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 11 | 336 | 1 | 19 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.810061e-03 |
solution =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 11
Feasible: "true"
Display all feasible solutions found during the approximation process.
displayfeasiblesolutions(solution)
| ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 1 | 784 | 1 | 47 | 16 | 16 | EvenSpacing | 7.812500e-03, 5.388912e-03 | | 2 | 768 | 1 | 46 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.534419e-03 | | 3 | 608 | 1 | 36 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.089765e-03 | | 4 | 592 | 1 | 35 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.272461e-03 | | 5 | 416 | 1 | 24 | 16 | 16 | EvenSpacing | 7.812500e-03, 6.201693e-03 | | 6 | 400 | 1 | 23 | 16 | 16 | EvenSpacing | 7.812500e-03, 6.958889e-03 | | 9 | 352 | 1 | 20 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.807773e-03 | | 11 | 336 | 1 | 19 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.810061e-03 | | 13 | 576 | 1 | 18 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.803448e-03 | | 15 | 576 | 1 | 18 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.803448e-03 | Best Solution | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 11 | 336 | 1 | 19 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.810061e-03 |
Solution with ID 5 is not listed as a feasible solution in the table. Explore this solution to see why it is not feasible.
solution5 = solutionfromID(solution, 5)
solution5 =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 5
Feasible: "true"
Compare the numerical behavior of the solution with ID 5.
compare(solution5)
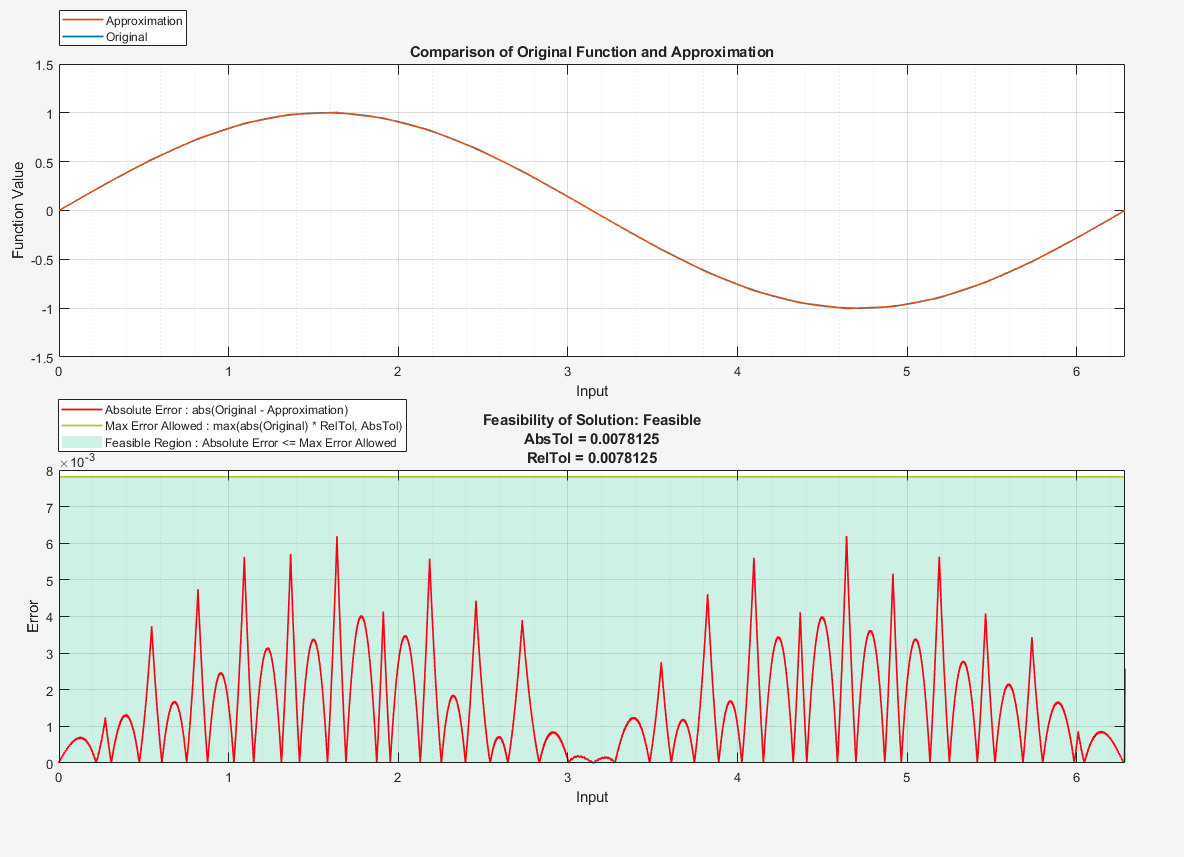
ans = struct with fields:
Breakpoints: [51473×1 double]
Original: [51473×1 double]
Approximate: [51473×1 double]
You can see from the plot that the solution does not meet the required tolerances.
Version History
Introduced in R2018a
See Also
Apps
Classes
FunctionApproximation.Problem|FunctionApproximation.Options|FunctionApproximation.LUTMemoryUsageCalculator|FunctionApproximation.LUTSolution
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)