threshold
Description
threshold creates threshold transitions from the specified levels and
transition type, either discrete or smooth. Use a threshold object to specify
the switching mechanism of a threshold-switching dynamic regression model (tsVAR).
To study a threshold transitions model, pass a fully specified threshold
object to an object function. You can specify
transition levels and rates as unknown parameters (NaN values), which you
can estimate when you fit a tsVAR model to data by using estimate.
Alternatively, to create a random switching mechanism, governed by a discrete-time Markov
chain, for a Markov-switching dynamic regression model, see dtmc and msVAR.
Creation
Description
tt = threshold(levels)tt for discrete state transitions specified by
the transition mid-levels levels.
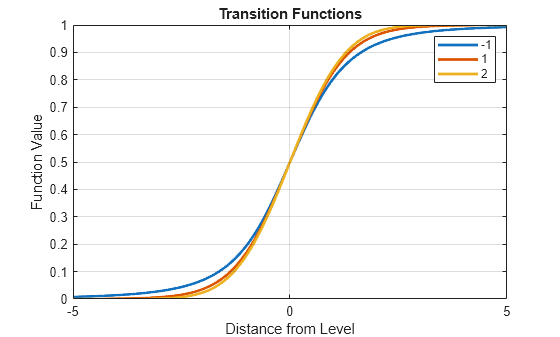
tt = threshold(levels,Name,Value)threshold([0
1],Type="exponential",Rates=[0.5 1.5]) specifies smooth, exponential
transitions at mid-levels 0 and 1 with rates
0.5 and 1.5, respectively.
Input Arguments
Properties
Object Functions
Examples
More About
Tips
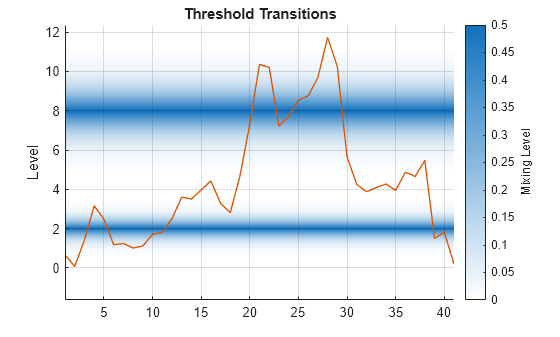
To widen a smooth transition band to show a more gradual mixing of states, decrease the transition rate by specifying the
Ratesname-value argument when you create threshold transitions.
References
Version History
Introduced in R2021b