Perform ARIMA Model Residual Diagnostics Using Econometric Modeler App

This example shows how to evaluate ARIMA model assumptions by performing residual diagnostics in the Econometric Modeler app. The data set, which is stored in Data_JAustralian.mat, contains the log quarterly Australian Consumer Price Index (CPI) measured from 1972 and 1991, among other time series.

Import Data into Econometric Modeler

At the command line, load the Data_JAustralian.mat data set.

load Data_JAustralian

Convert the table DataTable to a timetable:

1. Clear the row names of DataTable.

2. Convert the sampling times to a datetime vector.

3. Convert the table to a timetable by associating the rows with the sampling times in dates.

DataTable.Properties.RowNames = {};
dates = datetime(dates,'ConvertFrom','datenum',...
     'Format','ddMMMyyyy','Locale','en_US');
DataTable = table2timetable(DataTable,'RowTimes',dates);

At the command line, open the Econometric Modeler app.

econometricModeler

Alternatively, open the app from the apps gallery (see Econometric Modeler).

Import DataTable into the app:

1. On the Econometric Modeler tab, in the Import section, click .

2. In the Import Data dialog box, in the Import? column, select the check box for the DataTable variable.

3. Click Import.

The variables, including PAU, appear in the Time Series pane, and a time series plot containing all the series appears in the Time Series Plot(EXCH) figure window.

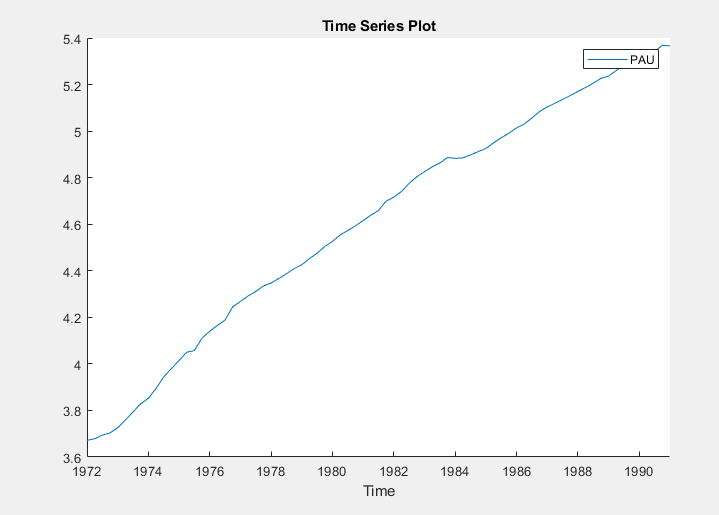
Create a time series plot of PAU by double-clicking PAU in the Time Series pane.

Specify and Estimate ARIMA Model

Estimate an ARIMA(2,1,0) model for the log quarterly Australian CPI (for details, see Implement Box-Jenkins Model Selection and Estimation Using Econometric Modeler App).

1. In the Time Series pane, select the PAU time series.

2. On the Econometric Modeler tab, in the Models section, click ARIMA.

3. In the ARIMA Model Parameters dialog box, on the Lag Order tab:

   1. Set the Degree of Integration to 1.

   2. Set the Autoregressive Order to 2.

   

4. Click Estimate.

The model variable ARIMA_PAU appears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(ARIMA_PAU) document.

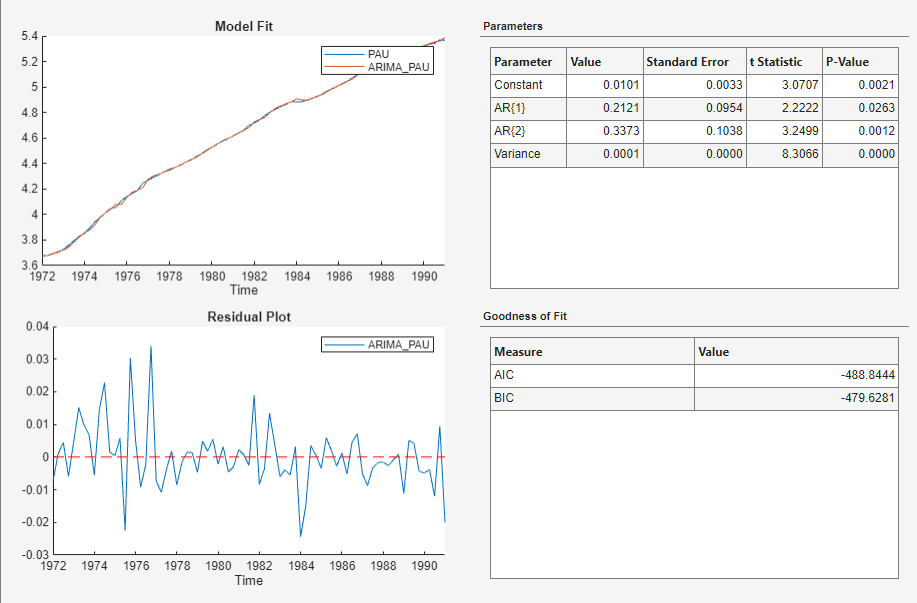
In the Model Summary(ARIMA_PAU) document, the Residual Plot figure is a time series plot of the residuals. The plot suggests that the residuals are centered at y = 0 and they exhibit volatility clustering.

Perform Residual Diagnostics

Visually assess whether the residuals are normally distributed by plotting their histogram and a quantile-quantile plot:

1. Close the Model Summary(ARIMA_PAU) document.

2. With ARIMA_PAU selected in the Models pane, on the Econometric Modeler tab, in the Diagnostics section, click Residual Diagnostics > Residual Histogram.

3. Click Residual Diagnostics > Residual Q-Q Plot.

Inspect the histogram by clicking the Histogram(ARIMA_PAU) figure window.

Inspect the quantile-quantile plot by clicking the QQPlot(ARIMA_PAU) figure window.

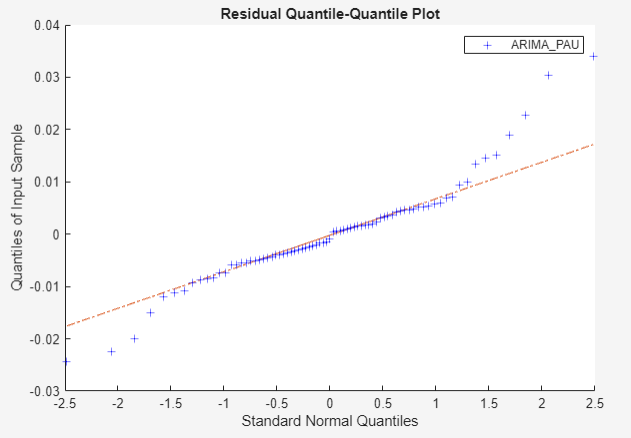
The residuals appear approximately normally distributed. However, there is an excess of large residuals, which indicates that a t innovation distribution might be a reasonable model modification.

Visually assess whether the residuals are serially correlated by plotting their autocorrelations. With ARIMA_PAU selected in the Models pane, in the Diagnostics section, click Residual Diagnostics > Autocorrelation Function.

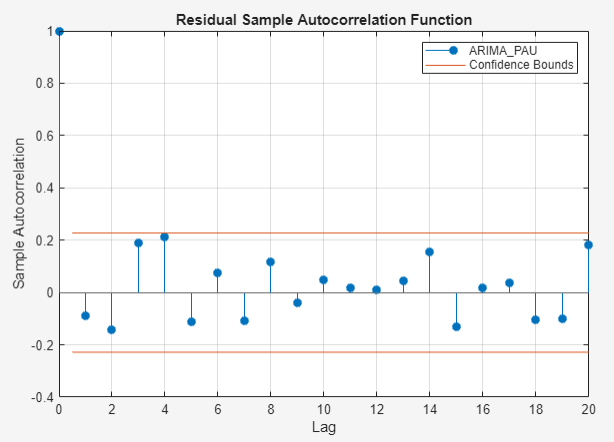
All lags that are greater than 0 correspond to insignificant autocorrelations. Therefore, the residuals are uncorrelated in time.

Visually assess whether the residuals exhibit heteroscedasticity by plotting the ACF of the squared residuals. With ARIMA_PAU selected in the Models pane, click the Econometric Modeler tab. Then, click the Diagnostics section, click Residual Diagnostics > Squared Residual Autocorrelation.

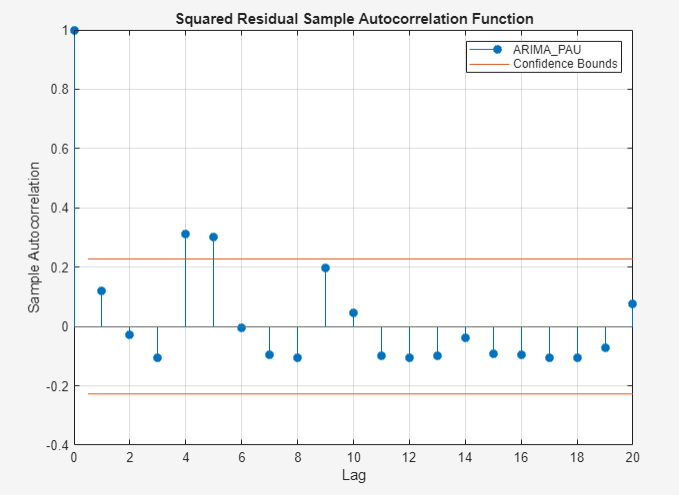
Significant autocorrelations occur at lags 4 and 5, which suggests a composite conditional mean and variance model for PAU.