collintest
Belsley collinearity diagnostics
Syntax
Description
[ displays, at the command window, Belsley collinearity diagnostics
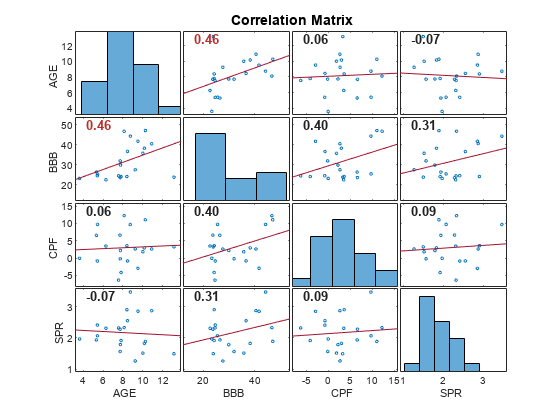
for assessing the strength and sources of collinearity among variables in the input matrix
of time series data. The function also returns the singular
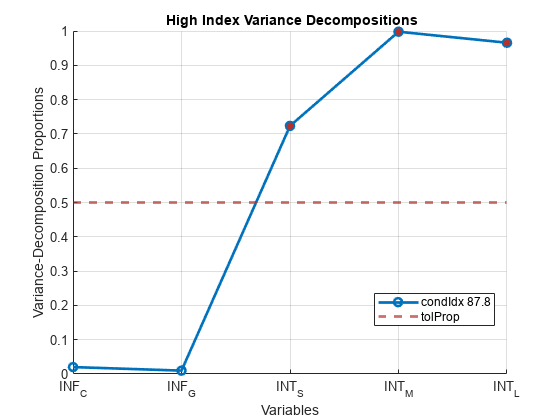
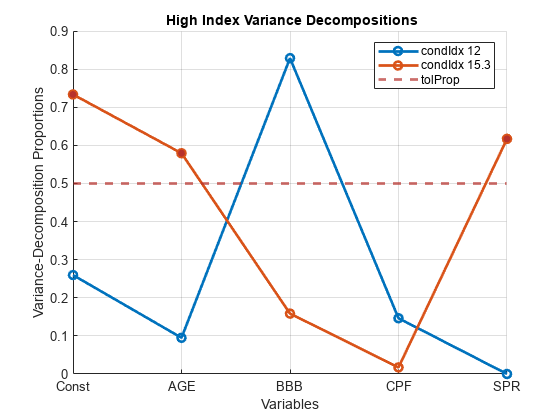
values in decreasing order, condition indices, and variance decomposition
proportions.sValue,condIdx,VarDecomp]
= collintest(X)
VarDecompTbl = collintest(Tbl)
To select a subset of variables, for which to compute collinearity diagnostics, use
the DataVariables name-value argument.
[___] = collintest(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)collintest returns the output argument combination for the
corresponding input arguments. For example,
collintest(Tbl,Plot="on",Display="off",DataVariables=1:5) plots the
Belslely collinearity diagnostics for the first 5 variables of the table
Tbl to a figure instead of the command window.
collintest(
plots on the axes specified by ax,Plot="on",___)ax instead of
the current axes (gca). ax can precede any of the input
argument combinations in the previous syntaxes.
[___,
plots the diagnostics of the input series and additionally returns handles to plotted
graphics objects h]
= collintest(___,Plot="on")h. Use elements of h to modify
properties of the plot after you create it.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
For purposes of collinearity diagnostics, Belsley [1] shows that column scaling of the design matrix composed of the input time series data is always desirable. However, he also shows that centering the data in
Xis undesirable. For models with an intercept, if you center the data inX, the role of the constant term in any near dependency is hidden, and yields misleading diagnostics.Tolerances for identifying large condition indices and variance-decomposition proportions are comparable to critical values in standard hypothesis tests. Experience determines the most useful tolerance, but experiments suggest the
collintestdefaults are good starting points [1].
References
[1] Belsley, D. A., E. Kuh, and R. E. Welsh. Regression Diagnostics. New York, NY: John Wiley & Sons, Inc., 1980.
[2] Judge, G. G., W. E. Griffiths, R. C. Hill, H. Lϋtkepohl, and T. C. Lee. The Theory and Practice of Econometrics. New York, NY: John Wiley & Sons, Inc., 1985.