smooth
Backward recursion of Bayesian nonlinear non-Gaussian state-space model
Since R2024a
Syntax
Description
smooth provides approximate posterior means and
covariances, conditioned on model parameters Θ and the full-sample response data, to summarize
the smoothing distribution of the state of a Bayesian nonlinear non-Gaussian state-space model
(bnlssm).
To compute the smoothed state distribution and likelihood,
smooth uses the forward-backward smoothing
method, in which it implements sequential Monte Carlo (SMC) to perform forward
filtering, and then it resamples and reweights particles (weighted
random samples) generated by SMC to perform backward smoothing.
[
returns approximate posterior means and covariances of the smoothing state distribution, for
each sampling time in the input response data, and the corresponding loglikelihood resulting
from performing backward recursion of, or smoothing, the input Bayesian nonlinear
state-space model. X,logL] = smooth(Mdl,Y,params)smooth evaluates the parameter map
Mdl.ParamMap by using the input vector of parameter values.
[
additionally returns smoothing results by sampling period using any of the input-argument
combinations in the previous syntaxes. X,logL,Output] = smooth(___)Output contains the following quantities:
Approximate loglikelihood values associated with the input data, input parameters, and particles
Approximate posterior means of smoothed state distribution
Approximate posterior covariance of smoothed state distribution
Effective sample size
Flags indicating which data the software used to smooth
Flags indicating resampling
Examples
This example uses simulated data to compute means of the approximate posterior smoothed state distribution of the following Bayesian nonlinear state-space model in equation. The state-space model contains two independent, stationary, autoregressive states each with a model constant. The observations are a nonlinear function of the states with Gaussian noise. The prior distribution of the parameters is flat. Symbolically, the system of equations is
and are the unconditional means of the corresponding states. The initial distribution moments of each state are their unconditional mean and covariance.
Create a Bayesian nonlinear state-space model characterized by the system. The observation equation is in equation form, that is, the function composing the states is nonlinear and the innovation series is additive, linear, and Gaussian. The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function and the prior distribution of the parameters. You can use the functions only within this script.
Mdl = bnlssm(@paramMap,@priorDistribution)
Mdl =
bnlssm with properties:
ParamMap: @paramMap
ParamDistribution: @priorDistribution
ObservationForm: "equation"
Multipoint: [1×0 string]
Mdl is a bnlssm model specifying the state-space model structure and prior distribution of the state-space model parameters. Because Mdl contains unknown values, it serves as a template for posterior analysis with observations.
Simulate a series of 100 observations from the following stationary 2-D VAR process.
where the disturbance series are standard Gaussian random variables.
rng(1,"twister") % For reproducibility T = 100; thetatrue = [0.9; 1; -0.75; -1; 0.3; 0.2; 0.1]; MdlSim = varm(AR={diag(thetatrue([1 3]))},Covariance=diag(thetatrue(5:6).^2), ... Constant=thetatrue([2 4])); XSim = simulate(MdlSim,T);
Compose simulated observations using the following equation.
where the innovation series is a standard Gaussian random variable.
ysim = log(sum(exp(XSim - mean(XSim)),2)) + thetatrue(7)*randn(T,1);
To compute means of the approximate posterior smoothed state distribution, the smooth function requires response data and a model with known state-space model parameters. Choose a random set with the following constraints:
and are within the unit circle. Use to generate values.
and are real numbers. Use the distribution to generate values.
, , and are positive real numbers. Use the distribution to generate values.
theta13 = (-1+(1-(-1)).*rand(2,1)); theta24 = 3*randn(2,1); theta567 = chi2rnd(1,3,1); theta = [theta13(1); theta24(1); theta13(2); theta24(2); theta567];
Compute approximate smoothed state posterior means and corresponding loglikelihood by passing the Bayesian nonlinear model, simulated data, and parameter values to smooth.
[SmoothX,logL] = smooth(Mdl,ysim,theta); size(SmoothX)
ans = 1×2
100 4
logL
logL = -134.1053
SmoothX is a 100-by-4 matrix of approximate smoothed state posterior means, with rows corresponding to periods in the sample and columns corresponding to the state variables. The smooth function uses the forward-backward smoothing method (SMC and simulation smoothing by default) to obtain draws from the posterior smoothed state distribution. logL is the approximate loglikelihood function estimate evaluated at the data and parameter values.
Compare the loglikelihood logL and the loglikelihood computed using from the data simulation.
[SmoothXSim,logLSim] = smooth(Mdl,ysim,thetatrue); logLSim
logLSim = -0.2036
logLSim > logL, suggesting that the model evaluated at thetaSim has the better fit.
Plot the two sets of approximate smoothed state posterior means with the true state values.
figure tiledlayout(2,1) nexttile plot([SmoothX(:,1) SmoothXSim(:,1) XSim(:,1)]) title("x_{t,1}") legend("Smoothed State, random \theta","Smoothed State, true \theta","XSim") nexttile plot([SmoothX(:,3) SmoothXSim(:,3) XSim(:,2)]) title("x_{t,3}") legend("Smoothed State, random \theta","Smoothed State, true \theta","XSim")
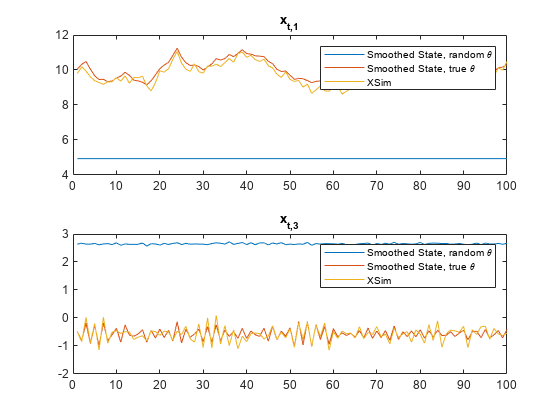
The approximate smoothed state posterior means using the true value of and the simulated state paths are close. The approximate smoothed state posterior means are far from the simulated state paths.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = @(x)blkdiag([theta(1) theta(2); 0 1],[theta(3) theta(4); 0 1])*x; B = [theta(5) 0; 0 0; 0 theta(6); 0 0]; C = @(x)log(exp(x(1)-theta(2)/(1-theta(1))) + ... exp(x(3)-theta(4)/(1-theta(3)))); D = theta(7); Mean0 = [theta(2)/(1-theta(1)); 1; theta(4)/(1-theta(3)); 1]; Cov0 = diag([theta(5)^2/(1-theta(1)^2) 0 theta(6)^2/(1-theta(3)^2) 0]); StateType = [0; 1; 0; 1]; % Stationary state and constant 1 processes end function logprior = priorDistribution(theta) paramconstraints = [(abs(theta([1 3])) >= 1) (theta(5:7) <= 0)]; if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
This example shows how to use smooth and Bayesian optimization to calibrate a Bayesian nonlinear state-space. Consider this nonlinear state-space model.
where has a flat prior and the series and are standard Gaussian random variables.
Simulate Series
Simulate a series of 100 observations from the following stationary 2-D VAR process.
where the series and are standard Gaussian random variables.
rng(500,"twister") % For reproducibility T = 100; thetaDGP = [0.5; 0.6; -1; 2; 0.75]; numparams = numel(thetaDGP); MdlSim = arima(AR=thetaDGP(1),Variance=thetaDGP(2).^2, ... Constant=0); xsim = simulate(MdlSim,T); ysim = exp(thetaDGP(3).*xsim) + thetaDGP(4) + thetaDGP(5)*randn(T,1);
Create Bayesian Nonlinear Model
Create a Bayesian nonlinear state-space model. The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function and the prior distribution of the parameters. You can use the functions only within this script. Specify Multipoint=["A" "C"] because the state-transition and measurement-sensitivity parameter mappings in paraMap can evaluate multiple particles simultaneously.
Mdl = bnlssm(@paramMap,@priorDistribution,Multipoint=["A" "C"]);
Perform Random Exploration
One way to explore the parameter space for the point that maximizes the likelihood is by random exploration:
Randomly generated set of parameters.
Compute the loglikelihood for that set derived from the approximate posterior smoothed state distribution. Generate 5000 particles for the SMC algorithm.
Repeat steps 1 and 2 for 100 epochs.
Choose the set of parameters that yields the largest loglikelihood.
Choose a random set using the following arbitrary recipe:
.
and are .
and are.
numepochs = 100; numparticles = 5000; theta = NaN(numparams,numepochs); logL = NaN(numepochs,1); for j = 1:numepochs theta(:,j) = [(-1+(1-(-1)).*rand(1,1)); chi2rnd(1,1,1); ... 2*randn(2,1); chi2rnd(1,1,1);]; [~,logL(j)] = smooth(Mdl,ysim,theta(:,j),NumParticles=numparticles); end
Choose the set of parameters that maximizes the loglikelihood.
[bestlogL,idx] = max(logL); bestTheta = theta(:,idx); [bestTheta thetaDGP]
ans = 5×2
0.1096 0.5000
1.8110 0.6000
-0.7610 -1.0000
1.5364 2.0000
0.9389 0.7500
The values that maximize the likelihood are fairly close to the values that generated the data.
Perform Bayesian Optimization
Bayesian optimization requires you to specify which variables require optimization and their support. To do this, use optimizableVariable to provide a name to the variable and its support. This example limits the support of each variable to a small interval; you must experiment with the support for your application.
thetaOp(5) = optimizableVariable("theta5",[0,2]); thetaOp(1) = optimizableVariable("theta1",[0,0.9]); thetaOp(2) = optimizableVariable("theta2",[0,2]); thetaOp(3) = optimizableVariable("theta3",[-3,0]); thetaOp(4) = optimizableVariable("theta4",[-3,3]);
thetaOp is an optimizableVariable object specifying the name and support of each variable of .
bayesopt accepts a function handle to the function that you want to minimize with respect to one argument and the optimizable variable specifications. Therefore, provide the function handle neglog, which is associated with the negative loglikelihood function smoothneglogl located in Local Functions. Specify the Expected Improvement Plus acquisition function and an exploration ratio of 1.
neglogl = @(var)smoothneglogl(var,Mdl,ysim,numparticles); rng(1,"twister") results = bayesopt(neglogl,thetaOp,AcquisitionFunctionName="expected-improvement-plus", ... ExplorationRatio=1);
|==================================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | theta1 | theta2 | theta3 | theta4 | theta5 |
| | result | | runtime | (observed) | (estim.) | | | | | |
|==================================================================================================================================================|
| 1 | Best | 1127.7 | 0.59077 | 1127.7 | 1127.7 | 0.0761 | 0.51116 | -0.78522 | -2.272 | 0.44888 |
| 2 | Best | 322.82 | 0.50186 | 322.82 | 369.77 | 0.5021 | 0.8957 | -0.11662 | -1.1518 | 1.8165 |
| 3 | Best | 245.8 | 0.11088 | 245.8 | 245.83 | 0.67392 | 0.54178 | -2.091 | -0.82814 | 0.63451 |
| 4 | Accept | 379.26 | 0.12438 | 245.8 | 245.99 | 0.74179 | 1.8872 | -1.9159 | -2.5691 | 1.596 |
| 5 | Best | 193.41 | 0.40948 | 193.41 | 193.61 | 0.60226 | 1.388 | -2.8719 | 1.8649 | 0.99824 |
| 6 | Accept | 378.94 | 0.11703 | 193.41 | 193.34 | 0.61122 | 1.7241 | -1.9549 | -2.7603 | 1.5881 |
| 7 | Best | 164.95 | 0.95914 | 164.95 | 164.99 | 0.89145 | 0.3939 | -0.86732 | 2.9996 | 1.13 |
| 8 | Accept | 175.33 | 0.43754 | 164.95 | 165.14 | 0.77039 | 1.1099 | -2.8749 | 2.9986 | 1.4799 |
| 9 | Accept | 188.55 | 0.59041 | 164.95 | 165.31 | 0.899 | 1.5766 | -2.7935 | 1.9077 | 1.4035 |
| 10 | Accept | 176.16 | 0.76174 | 164.95 | 165.82 | 0.89675 | 1.074 | -2.056 | 2.9966 | 1.7122 |
| 11 | Best | 162.35 | 0.67631 | 162.35 | 162.26 | 0.70663 | 0.021792 | -2.8874 | 2.4126 | 1.2572 |
| 12 | Accept | 167.12 | 1.1758 | 162.35 | 162.89 | 0.82297 | 0.0099343 | -2.8661 | 2.5609 | 1.3679 |
| 13 | Accept | 37507 | 0.43551 | 162.35 | 131.64 | 0.72519 | 0.019759 | -2.4419 | 2.7505 | 0.041092 |
| 14 | Accept | 1544.1 | 1.0636 | 162.35 | 171.69 | 0.61096 | 0.38246 | -0.30051 | -2.98 | 0.85496 |
| 15 | Accept | 196.22 | 0.46353 | 162.35 | 173.98 | 0.67033 | 0.88907 | -2.6327 | 2.4757 | 1.9997 |
| 16 | Accept | 221.1 | 0.19646 | 162.35 | 174.33 | 0.68492 | 0.41576 | -2.9961 | 0.1524 | 0.54823 |
| 17 | Accept | 331.59 | 0.2868 | 162.35 | 170.62 | 0.83362 | 1.8137 | -2.9992 | -0.77834 | 1.8933 |
| 18 | Accept | 170.22 | 0.47666 | 162.35 | 125 | 0.59515 | 0.42113 | -2.9034 | 2.9794 | 1.0632 |
| 19 | Accept | 216.94 | 0.53625 | 162.35 | 126.1 | 0.3111 | 0.84077 | -1.3483 | 2.9564 | 0.5773 |
| 20 | Accept | 177.18 | 0.2597 | 162.35 | 154.22 | 0.3466 | 0.42928 | -2.9798 | 1.6888 | 0.25124 |
|==================================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | theta1 | theta2 | theta3 | theta4 | theta5 |
| | result | | runtime | (observed) | (estim.) | | | | | |
|==================================================================================================================================================|
| 21 | Accept | 185.07 | 0.4398 | 162.35 | 154.2 | 0.00115 | 0.093713 | -1.8586 | 2.7626 | 1.9993 |
| 22 | Accept | 271.9 | 0.18641 | 162.35 | 153.64 | 0.0080476 | 0.37377 | -2.9919 | -0.27248 | 0.1696 |
| 23 | Accept | 369.97 | 0.11158 | 162.35 | 160.63 | 0.28982 | 1.2793 | -2.9778 | -1.244 | 0.38512 |
| 24 | Accept | 171.4 | 0.36413 | 162.35 | 160.02 | 0.0058968 | 0.41891 | -0.51186 | 2.6739 | 1.4408 |
| 25 | Accept | 644.44 | 0.92282 | 162.35 | 162.18 | 0.079409 | 0.32809 | -1.219 | 2.9808 | 0.30693 |
| 26 | Accept | 198.03 | 0.36622 | 162.35 | 162.75 | 0.0065223 | 1.0531 | -2.964 | 2.899 | 0.96624 |
| 27 | Accept | 339.01 | 0.13049 | 162.35 | 161.93 | 0.15558 | 0.84882 | -2.9909 | -2.1498 | 1.7239 |
| 28 | Accept | 327.16 | 0.11923 | 162.35 | 161.54 | 0.23219 | 0.48289 | -2.9966 | -2.3966 | 1.2154 |
| 29 | Accept | 199.37 | 0.25693 | 162.35 | 161.18 | 0.29476 | 0.83904 | -1.7824 | 1.7096 | 1.9978 |
| 30 | Accept | 363.59 | 0.099403 | 162.35 | 192.75 | 0.51879 | 0.97684 | -2.9991 | -2.1266 | 0.52726 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 19.377 seconds
Total objective function evaluation time: 13.1709
Best observed feasible point:
theta1 theta2 theta3 theta4 theta5
_______ ________ _______ ______ ______
0.70663 0.021792 -2.8874 2.4126 1.2572
Observed objective function value = 162.3519
Estimated objective function value = 164.8136
Function evaluation time = 0.67631
Best estimated feasible point (according to models):
theta1 theta2 theta3 theta4 theta5
_______ ________ _______ ______ ______
0.00115 0.093713 -1.8586 2.7626 1.9993
Estimated objective function value = 192.7467
Estimated function evaluation time = 0.43707

results is a BayesianOptmization object containing properties summarizing the results of Bayesian optimization.
Extract the value that minimizes the negative loglikelihood from results by using bestPoint.
restbl = [bestPoint(results); num2cell(thetaDGP')]; restbl.Properties.RowNames = ["calibrated" "true"]
restbl=2×5 table
theta1 theta2 theta3 theta4 theta5
_______ ________ _______ ______ ______
calibrated 0.00115 0.093713 -1.8586 2.7626 1.9993
true 0.5 0.6 -1 2 0.75
The results are fairly close to the values that generated the data.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and the log prior distribution of the parameters, and they compute the negative loglikelihood of the model.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = @(x)theta(1)*x; B = theta(2); C = @(x)exp(theta(3).*x) + theta(4); D = theta(5); Mean0 = 0; Cov0 = 1; StateType = 0; % Stationary state process end function logprior = priorDistribution(theta) paramconstraints = [abs(theta(1)) >= 1; theta([2 4]) <= 0]; if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end function neglogL = smoothneglogl(theta,mdl,resp,np) theta = table2array(theta); [~,logL] = smooth(mdl,resp,theta,NumParticles=np); neglogL = -logL; end
smooth runs SMC to forward filter the state-space model, which includes resampling particles. To assess the quality of the sample, including whether any posterior smoothed state distribution is close to degenerate, you can monitor these algorithms by returning the third output of smooth.
Consider this nonlinear state-space model.
where has a flat prior and the series and are standard Gaussian random variables.
Simulate a series of 100 observations from the following stationary 2-D VAR process.
where the series and are standard Gaussian random variables.
rng(500,"twister") % For reproducibility T = 100; thetaDGP = [0.5; 0.6; -1; 2; 0.75]; numparams = numel(thetaDGP); MdlSim = arima(AR=thetaDGP(1),Variance=sqrt(thetaDGP(2)), ... Constant=0); xsim = simulate(MdlSim,T); y = exp(thetaDGP(3).*xsim) + thetaDGP(4) + thetaDGP(5)*randn(T,1);
Create a Bayesian nonlinear state-space model, and specify Multipoint=["A" "C"]. The Local Functions section contains the required functions specifying the Bayesian nonlinear state-space model structure and joint prior distribution.
Mdl = bnlssm(@paramMap,@priorDistribution,Multipoint=["A" "C"]);
Approximate the posterior smoothed state distribution of the state-space model. As in the Calibrate State-Space Model Parameters example, choose a random set of initial parameter values. Specify the resampling residuals for the SMC. Return the third output.
theta0 = [(-1+(1-(-1)).*rand(1,1)); chi2rnd(1,1,1); ... 2*randn(2,1); chi2rnd(1,1,1);]; [~,~,Output] = smooth(Mdl,y,theta0,Resample="residual");
Output is a 100-by-1 structure array containing several fields, one set of fields for each observation, including:
SmoothedStatesCov— Approximate posterior smoothed state distribution covariance for the states at each sampling timeDataUsed— Whethersmoothused an observation for posterior estimationResample— Whethersmoothresampled the particles associated with an observation
Plot the approximate posterior smoothed state covariances.
figure
plot([Output.SmoothedStatesCov])
title("Approx. Post. Smoothed State Covariances")
Any covariance close to 0 indicates a close-to-degenerate distribution. No covariances in the analysis are close to 0.
Determine whether smooth omitted any observations from posterior estimation.
anyObsOmitted = sum([Output.DataUsed]) ~= T
anyObsOmitted = logical
0
anyObsOmitted = 0 indicates that smooth used all observations.
Determine whether smooth resampled any particles associated with observations.
whichResampled = find([Output.Resampled] == true)
whichResampled = 1×2
37 56
smooth resampled particles associated with observations 37 and 56.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and the log prior distribution of the parameters, and they compute the negative loglikelihood of the model.
function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta) A = @(x)theta(1)*x; B = theta(2); C = @(x)exp(theta(3).*x) + theta(4); D = theta(5); Mean0 = 0; Cov0 = 1; StateType = 0; % Stationary state process end function logprior = priorDistribution(theta) paramconstraints = [abs(theta(1)) >= 1; theta([2 4]) <= 0]; if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
This example compares the performance of several SMC proposal particle resampling methods for obtaining smoothed state estimates of a quasi-nonnegative constrained state space model, which models nonnegative state quantities such as interest rates and prices:
and are iid standard Gaussian random variables.
Generate Artificial Data
Consider the following data-generating process (DGP)
Generate a random series of 200 observations from the DGP.
a0 = 0.1; a1 = 0.95; b = 1; d = 0.5; theta = [a0; a1; b; d]; T = 50; % Preallocate variables x = zeros(T,1); y = zeros(T,1); rng(0,"twister") % For reproducibility u = randn(T,1); e = randn(T,1); for t = 2:T x(t) = max(0,a0 + a1*x(t-1)) + b*u(t); y(t) = x(t) + d*e(t); end
Create Bayesian Nonlinear State-Space Model
The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function paramMap and the prior distribution of the parameters priorDistribution. You can use the functions only within this script.
The paramMap function has these qualities:
Functions can simultaneously evaluate the state equation for multiple values of
A. Therefore, you can speed up calculations by specifying theMultipoint="A"option.The observation equation is in equation form, that is, the function composing the states is nonlinear and the innovation series is additive, linear, and Gaussian.
The priorDistribution function specifies a flat prior, which has a density that is proportional to 1 everywhere in the parameter space; it constrains the error standard deviations to be positive.
Create a Bayesian nonlinear state-space model characterized by the system.
Mdl = bnlssm(@paramMap,@priorDistribution,Multipoint="A");Obtain Smoothed State Estimates Using Each Proposal Sampler Method
Obtain smoothed state estimates using the joint distribution of the parameters, at a randomly drawn set of values in [0,1], using the bootstrap, optimal, and one-pass unscented particle resampling methods. Specify drawing 5000 particles for SMC.
numParticles = 5000; params = rand(4,1); smcMethod = ["bootstrap" "optimal" "unscented"]; for j = 3:-1:1 % Set last element first to preallocate entire cell vector xSmooth{j} = smooth(Mdl,y,params,NewSamples=smcMethod(j),NumParticles=numParticles); end
Compare the posterior means from each method with the true values.
figure tiledlayout(3,1) for j = 1:3 nexttile plot([x xSmooth{j}]) title("SMC Method: " + upper(smcMethod(j))) end legend("True","Smooth")
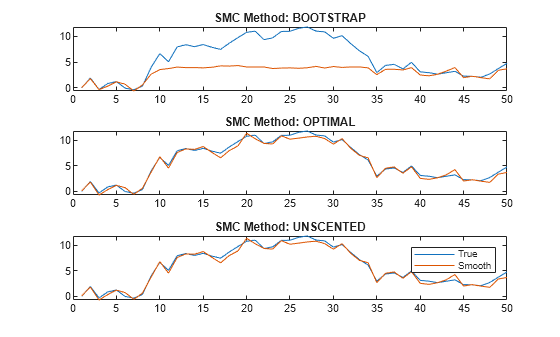
The figure shows that, in this case, the optimal and one-pass unscented methods yield smoothed state estimates closer to the true values than the bootstrap method. For the bootstrap method, smoothed state estimates in periods 10 through 35 level off around 5, while the true values jump as high as 10. The reason is the bootstrap filter updates particles solely by the transition equation—observations do not inform how particles are updated unlike the optimal and unscented methods.
Regardless of method, smooth weighs particles by the observation densities. In this example, the observation equation is (as specified in params). For the bootstrap filter, the normally distributed observation innovation, with small loading 0.17, cannot accommodate large jumps, such as from 5 to 10. Consequently, the weights are degenerate: the largest particle takes all the weight, and smooth discards the remaining particles during resampling because they have zero weight. The smoothed states level off until period 35 when the observations fall below 5.
Local Functions
These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.
function [A,B,C,D,mean0,Cov0] = paramMap(params) a0 = params(1); a1 = params(2); b = params(3); d = params(4); A = @(x) max(0,a0+a1.*x); B = b; C = 1; D = d; mean0 = 0; Cov0 = 1; end function logprior = priorDistribution(theta) paramconstraints = theta(3:4) <= 0; % b and d are greater than 0 if(sum(paramconstraints)) logprior = -Inf; else logprior = 0; % Prior density is proportional to 1 for all values % in the parameter space. end end
Input Arguments
Observed response data, specified as a numeric matrix or a cell vector of numeric vectors.
If
Mdlis time invariant with respect to the observation equation,Yis a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row ofYcontains the latest observations.If
Mdlis time varying with respect to the observation equation,Yis a T-by-1 cell vector.Y{t}contains an nt-dimensional vector of observations for period t, where t = 1, ..., T. For linear observation models, the corresponding dimensions of the coefficient matrices, outputs ofMdl.ParamMap,C{t}, andD{t}must be consistent with the matrix inY{t}for all periods. For nonlinear observation models, the dimensions of the inputs and outputs associated with the observations must be consistent. Regardless of model type, the last cell ofYcontains the latest observations.
NaN elements indicate missing observations. For details on how
smooth accommodates missing observations, see Algorithms.
Data Types: double | cell
State-space model parameters Θ to evaluate the parameter mapping
Mdl.ParamMap, specified as a numparams-by-1
numeric vector. Elements of params must correspond to the elements of
the first input arguments of Mdl.ParamMap and
Mdl.ParamDistribution.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: smooth(Mdl,Y,params,NumParticles=1e4,Resample="residual")
specifies 1e4 particles for the SMC routine and to resample
residuals.
Forward-backward smoothing method, specified as a value in this table.
| Value | Description |
|---|---|
"marginal" |
You can tune the forward-filtering algorithm by setting the
|
"simsmooth" | smooth dispatches to
simsmooth to approximate the mean and covariance of
the posterior smoothed state distribution by generating sample paths using
the simulation smoother. In addition to the arguments for tuning the
forward-filtering algorithm, you can tune the simulation smoother by setting
the NumPaths and MaxIterations
name-value arguments. For details, see simsmooth. |
"simsmooth" and "marginal" algorithms are
computationally intensive; both have complexity
O(NumParticles2T).
Their speed and accuracy is application dependent. It is good practice to experiment
with both algorithms and tune the associated parameters as needed.
Example: Method="marginal"
Data Types: char | string
Number of particles for SMC, specified as a positive integer.
Example: NumParticles=1e4
Data Types: double
Since R2025a
SMC proposal (importance) distribution, specified as a value in this table.
| Value | SMC Sampler | Description |
|---|---|---|
"bootstrap" | Bootstrap forward filter [7] | SMC samples particles form the state transition distribution (observations do not inform the sampler). This option
is available only for models with observation noise (nonzero
This method has a relatively low computational cost, but it does not inform the routine of the current observations, which can increase the Monte Carlo sampling variance. |
"optimal" | Conditionally optimal proposal [4] | SMC samples particles from the one-step filtering distribution with incremental weights proportional to the likelihood (observations inform the sampler). The weights have minimum variance. This option is available for the following tractable models supplied in equation form:
|
"unscented" | Unscented transformation [9] | SMC proposal distribution is the one-step filtering distribution approximated by the unscented transformation (observations inform the sampler). This option is
available only for models in equation form with observation noise
(nonzero By default, this option
uses the filtered state mean as the representative point, around
which the algorithm generates sigma points. To specify all particles
as representative points for the unscented transformation, set
|
Example: NewSamples="unscented"
Data Types: char | string
Since R2025a
Flag to apply unscented transformation to all particles, specified as a value in this table.
| Value | Description |
|---|---|
false | The filtered state mean is the representative point, around which the algorithm generates sigma points. This
option is less computationally expensive than
|
true | All particles are the representative points. This option is more computationally expensive than the default, but it can yield a higher-quality proposal distribution. |
Example: MultiPassUnscented=false
Data Types: logical
Number of sample state paths to generate for the simulation smoother, specified as
a positive integer. smooth ignores this argument when
Method is "marginal".
Example: NumPaths=10000
Data Types: double
Maximum number of rejection sampling iterations for posterior sampling using the simulation smoother, specified as a nonnegative integer. smooth conducts rejection sampling before it conducts the computationally intensive importance sampling algorithm.
smooth ignores this argument when
Method is "marginal".
Example: MaxIterations=100
Data Types: double
SMC resampling method, specified as a value in this table.
| Value | Description |
|---|---|
"multinomial" | At time t, the set of previously generated particles (parent set) follows a standard multinomial distribution, with probabilities proportional to their weights. An offspring set is resampled with replacement from the parent set [1]. |
"residual" | Residual sampling, a modified version of multinomial resampling that can produce an estimator with lower variance than the multinomial resampling method [8]. |
"systematic" | Systematic sampling, which produces an estimator with lower variance than the multinomial resampling method [3]. |
Resampling methods downsample insignificant particles to achieve a smaller estimator variance than if no resampling is performed and to avoid sampling from a degenerate proposal [5].
Example: Resample="residual"
Data Types: char | string
Effective sample size threshold, below which smooth resamples particles, specified as a nonnegative scalar. For more details, see [5], Ch. 12.3.3.
Tip
To resample during every period, set
Cutoff=numparticles, wherenumparticlesis the value of theNumParticlesname-value argument.To avoid resampling, set
Cutoff=0.
Example: Cutoff=0.75*numparticles
Data Types: double
Flag for sorting particles before resampling, specified as a value in this table.
| Value | Description |
|---|---|
true | smooth sorts the generated particles before resampling them. |
false | smooth does not sort the generated particles. |
When SortPartiles=true, smooth uses Hilbert sorting during the SMC routine to sort the particles. This action can reduce Monte Carlo variation, which is useful when you compare loglikelihoods resulting from evaluating several params arguments that are close to each other [3]. However, the sorting routine requires more computation resources, and can slow down computations, particularly in problems with a high-dimensional state variable.
Example: SortParticles=true
Data Types: logical
Output Arguments
Approximate smoothed state estimates E(xt|y1,…,yT), for t = 1,…,T, returned as a T-by-m numeric matrix or a T-by-1 cell vector of numeric vectors.
Each row corresponds to a time point in the sample. The last row contains the latest smoothed states.
For time-invariant models, smooth returns a matrix. Each
column corresponds to a state variable
xt.
If Mdl is time varying, X is a cell vector.
Cell t contains a column vector of smoothed state estimates with
length mt. Each column corresponds to a state
variable.
Approximate loglikelihood function value log p(y1,…,yT).
The loglikelihood value has noise induced by SMC.
Missing observations do not contribute to the loglikelihood.
Smoothing results by sampling time, returned as a structure array.
Output is a T-by-1 structure, where element
t corresponds to the smoothing result for time
t.
| Field | Description | Estimate/Approximation of |
|---|---|---|
LogLikelihood | Scalar approximate loglikelihood objective function value | log p(yt|y1,…,yt) |
SmoothedStates | mt-by-1 vector of approximate smoothed state estimates | |
SmoothedStatesCov | mt-by-mt variance-covariance matrix of smoothed states | |
EffectiveSampleSize | Effective sample size for importance sampling, a scalar in
[0,NumParticles] | N/A |
DataUsed | ht-by-1 flag indicating whether
the software smooths using a particular observation. For example, if
observation j at time t is a
NaN, element j in
DataUsed at time t is
0. | N/A |
Resampled | Flag indicating whether smooth resampled
particles | N/A |
Tips
Smoothing has several advantages over filtering.
The smoothed state estimator is more accurate than the online filter state estimator because it is based on the full-sample data, rather than only observations up to the estimated sampling time.
A stable approximation to the gradient of the loglikelihood function, which is important for numerical optimization, is available from the smoothed state samples of the simulation smoother (finite differences of the approximated loglikelihood computed from the filter state estimates is numerically unstable).
You can use the simulation smoother to perform Bayesian estimation of the nonlinear state-space model via the Metropolis-within-Gibbs sampler.
Unless you set
Cutoff=0,smoothresamples particles according to the specified resampling methodResample. Although resampling particles with high weights improves the results of the SMC, you should also allow the sampler traverse the proposal distribution to obtain novel, high-weight particles. To do this, experiment withCutoff.Avoid an arbitrary choice of the initial state distribution.
bnlssmfunctions generate the initial particles from the specified initial state distribution, which impacts the performance of the nonlinear filter. If the initial state specification is bad enough, importance weights concentrate on a small number of particles in the first SMC iteration, which might produce unreasonable filtering results. This vulnerability of the nonlinear model behavior contrasts with the stability of the Kalman filter for the linear model, in which the initial state distribution usually has little impact on the filter because the prior is washed out as it processes data.
Algorithms
smooth accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.
Alternative Functionality
To monitor the forward-filtering stage or to conduct a Gibbs sampler, use simsmooth instead of
smooth.
References
[1] Andrieu, Christophe, Arnaud Doucet, and Roman Holenstein. "Particle Markov Chain Monte Carlo Methods." Journal of the Royal Statistical Society Series B: Statistical Methodology 72 (June 2010): 269–342. https://doi.org/10.1111/j.1467-9868.2009.00736.x.
[2] Andrieu, Christophe, and Gareth O. Roberts. "The Pseudo-Marginal Approach for Efficient Monte Carlo Computations." Ann. Statist. 37 (April 2009): 697–725. https://dx.doi.org/10.1214/07-AOS574.
[3] Deligiannidis, George, Arnaud Doucet, and Michael Pitt. "The Correlated Pseudo-Marginal Method." Journal of the Royal Statistical Society, Series B: Statistical Methodology 80 (June 2018): 839–870. https://doi.org/10.1111/rssb.12280.
[4] Doucet, Arnaud, Simon Godsill, and Christophe Andrieu. "On Sequential Monte Carlo Sampling Methods for Bayesian Filtering." Statistics and Computing 10 (July 2000): 197–208. https://doi.org/10.1023/A:1008935410038.
[5] Durbin, J, and Siem Jan Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.
[6] Fernández-Villaverde, Jesús, and Juan F. Rubio-Ramírez. "Estimating Macroeconomic Models: A Likelihood Approach." Review of Economic Studies 70(October 2007): 1059–1087. https://doi.org/10.1111/j.1467-937X.2007.00437.x.
[7] Gordon, Neil J., David J. Salmond, and Adrian F. M. Smith. "Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation." IEE Proceedings F Radar and Signal Processing 140 (April 1993): 107–113. https://doi.org/10.1049/ip-f-2.1993.0015.
[8] Liu, Jun, and Rong Chen. "Sequential Monte Carlo Methods for Dynamic Systems." Journal of the American Statistical Association 93 (September 1998): 1032–1044. https://dx.doi.org/10.1080/01621459.1998.10473765.
[9] van der Merwe, Rudolph, Arnaud Doucet, Nando de Freitas, and Eric Wan. "The Unscented Particle Filter." Advances in Neural Information Processing Systems 13 (November 2000). https://dl.acm.org/doi/10.5555/3008751.3008833.
Version History
Introduced in R2024aWhile the SMC routine implements forward filtering, it resamples particles to align them to
the target distribution. The NewSamples name-value argument enables you
to choose how the SMC sampler chooses the particles. The supported algorithms are the
bootstrap forward filter ("bootstrap"), the conditionally optimal
proposal ("optimal"), and the unscented transformation
("unscented).
By default, the unscented transformation uses the filtered state mean as the representative
point, around which sigma points are generated. The MultiPassUnscented
name-value argument enables you to specify all particles as representative points for the
unscented transformation.
Before R2025a, the functions implement forward filtering using only the bootstrap filter.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)