bkfilter

Baxter-King filter for trend and cyclical components

Since R2023a

Syntax

[Trend,Cyclical] = bkfilter(Y)

[TTbl,CTbl] = bkfilter(Tbl)

[___] = bkfilter(___,Name=Value)

bkfilter(___)

bkfilter(ax,___)

[___,h] = bkfilter(___)

Description

The bkfilter function applies the Baxter-King filter to separate one or more time series into additive trend and cyclical components. bkfilter optionally plots the series and smoothed trend component, with cycles removed.

In addition to the Baxter-King filter, Econometrics Toolbox™ supports the Christiano-Fitzgerald (cffilter), Hamilton (hfilter), and Hodrick-Prescott (hpfilter) filters.

[Trend,Cyclical] = bkfilter(Y) returns the additive trend and cyclical components from applying the Baxter-King filter [1] to each variable (column) of the input matrix of time series data, using the definition of a business cycle in [2] for quarterly data.

[TTbl,CTbl] = bkfilter(Tbl) returns tables or timetables containing variables for the trend and cyclical components from applying the Baxter-King filter to each variable in an input table or timetable. To select different variables to filter, use the DataVariables name-value argument.

[___] = bkfilter(___,Name=Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. bkfilter returns the output argument combination for the corresponding input arguments. For example, bkfilter(Tbl,Stationarity=true,DataVariables=1:5) applies the Baxter-King filter to the first five variables in the input table Tbl and specifies at all input series are stationary.

bkfilter(___) plots time series variables in the input data and their respective smoothed trend components (cycles removed), computed by the Baxter-King filter, on the same axes.

bkfilter(ax,___) plots on the axes specified by ax instead of the current axes (gca). ax can precede any of the input argument combinations in the previous syntaxes.

[___,h] = bkfilter(___) plots the specified series and their trend components, and additionally returns handles to plotted graphics objects. Use elements of h to modify properties of the plot after you create it.

Examples

Apply Baxter-King Filter to Matrix of Data

Plot the cyclical component of the US post-WWII, seasonally adjusted, quarterly, real gross national product (GNPR).

load Data_GNP
GNPR = Data(:,2);
[trend,cyclical] = bkfilter(GNPR);
T = numel(trend)

T = 
235

trend and cyclical are 235-by-1 vectors containing the trend and cyclical components, respectively, resulting from applying the Baxter-King filter to the series with default upper and lower cutoffs, and lag length for the filter moving average. The first and last 12 values are NaNs.

plot(dates,cyclical) 
axis tight
ylabel("Real GNP Cyclical Component")

Apply Baxter-King Filter to Table Variables

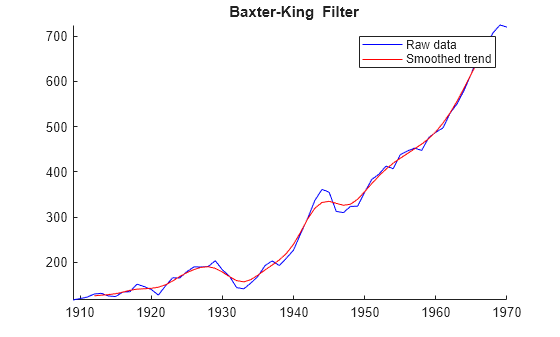
Apply the Baxter-King filter to all variables in input table variables.

Load the Schwert stock data set Data_SchwertStock.mat, which contains monthly returns of the NYSE index from 1871 through 2008 in DataTimeTableMth, among three other variables (for details, enter Description). Remove all missing observations from all series.

load Data_SchwertStock
TTM = rmmissing(DataTimeTableMth);

Aggregate the monthly data in the timetable to quarterly measurements.

TTQ = convert2quarterly(TTM);

Apply the Baxter-King filter to all variables in the quarterly timetable. Use the default cutoffs and lag length for the moving average.

[TQTT,CQTT] = bkfilter(TTQ);
size(TQTT)

ans = 1×2

   220     4

TQTT and CQTT are 220-by-4 timetables containing the trend and cyclical components, respectively, of the series in TTQ. Variables in the input and output timetables correspond. By default, bkfilter filters all variables in the input table or timetable. To select a subset of variables, set the DataVariables option.

The default lag length is 12. Consequently, the first and last 12 rows in the output timetable are NaN-valued.

Remove the leading and lagging NaNs from the trends and display what remains.

TQTTCut = rmmissing(TQTT);
CQTTCut = rmmissing(CQTT);
TQTTCut

TQTTCut=196×4 timetable
       Time          Return       DivYld       CapGain       CapGainA 
    ___________    __________    _________    __________    __________

    31-Mar-1874     -0.039822    0.0032538     -0.028711     -0.043076
    30-Jun-1874     -0.017105    0.0044321     -0.023919     -0.021537
    30-Sep-1874     0.0039487    0.0010179      0.002954     0.0029307
    31-Dec-1874    -0.0078419    0.0050448    -0.0063275     -0.012887
    31-Mar-1875      0.020326    0.0024432      0.015128      0.017883
    30-Jun-1875    -0.0020712    0.0038703     -0.017158    -0.0059416
    30-Sep-1875    -0.0085514    0.0044146      -0.01171     -0.012966
    31-Dec-1875     -0.006103    0.0036185    -0.0058395    -0.0097214
    31-Mar-1876    -0.0055681    0.0031237    -0.0059341    -0.0086918
    30-Jun-1876      0.013271    0.0044001     0.0034571     0.0088705
    30-Sep-1876     -0.033603    0.0042907      -0.03317     -0.037894
    31-Dec-1876       0.04053    0.0045942      0.031644      0.035936
    31-Mar-1877     0.0023469    0.0032843     -0.014032    -0.0009374
    30-Jun-1877     -0.061762     0.004893     -0.049214     -0.066655
    30-Sep-1877      0.066959    0.0047892      0.058975       0.06217
    31-Dec-1877     -0.017554    0.0029106     -0.026179     -0.020464
      ⋮

CQTTCut

CQTTCut=196×4 timetable
       Time          Return        DivYld        CapGain       CapGainA 
    ___________    __________    ___________    __________    __________

    31-Mar-1874       0.01699       -0.00117      0.015758       0.01816
    30-Jun-1874      0.020025     -0.0013329      0.018379      0.021358
    30-Sep-1874      0.016201    -0.00079002      0.013713      0.016991
    31-Dec-1874     0.0064867     1.9907e-06     0.0036027     0.0064847
    31-Mar-1875     -0.002434     0.00036989    -0.0041687    -0.0028039
    30-Jun-1875    -0.0061591     3.1258e-05    -0.0050638    -0.0061903
    30-Sep-1875    -0.0033857    -0.00076308    0.00044226    -0.0026226
    31-Dec-1875     0.0015781     -0.0013475     0.0058395     0.0029255
    31-Mar-1876     0.0017405     -0.0010938     0.0031869     0.0028343
    30-Jun-1876    -0.0062558     1.9708e-05    -0.0094095    -0.0062755
    30-Sep-1876     -0.021212      0.0013923     -0.026956     -0.022604
    31-Dec-1876     -0.034671      0.0023024      -0.03854     -0.036974
    31-Mar-1877     -0.039779      0.0023122     -0.038012     -0.042091
    30-Jun-1877     -0.028847      0.0017301     -0.022516     -0.030577
    30-Sep-1877     -0.003445      0.0011069     0.0022493    -0.0045519
    31-Dec-1877      0.023547     0.00090623      0.022362      0.022641
      ⋮

To compare outputs between different tabular inputs, apply the Baxter-King filter to all variables in the table of monthly data DataTableMth and the timetable of monthly data TTM.

% Table input of monthly data
DTM = rmmissing(DataTableMth);
[TMDT,CMDT] = bkfilter(DataTableMth);
TMDT = rmmissing(TMDT);
CMDT = rmmissing(CMDT);
size(TMDT)

ans = 1×2

   632     4

tail(TMDT)

                 Return       DivYld       CapGain       CapGainA 
               __________    _________    __________    __________

    May1924    -0.0016302     0.002973    -0.0046032    -0.0046032
    Jun1924      0.047692    0.0065778      0.041115      0.041115
    Jul1924      0.044844    0.0060522      0.038792      0.038792
    Aug1924      0.010929    0.0019358     0.0089936     0.0089936
    Sep1924    -0.0086959     0.006971     -0.015667     -0.015667
    Oct1924    -0.0014852    0.0049456    -0.0064308    -0.0064308
    Nov1924      0.062927    0.0020931      0.060834      0.060834
    Dec1924      0.045108    0.0070319      0.038076      0.038076

tail(CMDT)

                Return        DivYld        CapGain     CapGainA 
               _________    ___________    _________    _________

    May1924    0.0074662    -4.9042e-05    0.0075152    0.0075152
    Jun1924     0.017044     0.00019971     0.016844     0.016844
    Jul1924     0.016657     0.00028124     0.016376     0.016376
    Aug1924    0.0096193     0.00019693    0.0094224    0.0094224
    Sep1924    0.0035508     0.00014389    0.0034069    0.0034069
    Oct1924    0.0064063     7.9476e-05    0.0063268    0.0063268
    Nov1924     0.013666     7.2083e-05     0.013594     0.013594
    Dec1924     0.015515     0.00010861     0.015407     0.015407

% Timetable input of monthly data
[TMTT,CMTT] = bkfilter(TTM);
TMTT = rmmissing(TMTT);
CMTT = rmmissing(CMTT);
size(TMTT)

ans = 1×2

   632     4

tail(TMTT)

       Time          Return       DivYld       CapGain       CapGainA 
    ___________    __________    _________    __________    __________

    01-May-1924    -0.0016302     0.002973    -0.0046032    -0.0046032
    01-Jun-1924      0.047692    0.0065778      0.041115      0.041115
    01-Jul-1924      0.044844    0.0060522      0.038792      0.038792
    01-Aug-1924      0.010929    0.0019358     0.0089936     0.0089936
    01-Sep-1924    -0.0086959     0.006971     -0.015667     -0.015667
    01-Oct-1924    -0.0014852    0.0049456    -0.0064308    -0.0064308
    01-Nov-1924      0.062927    0.0020931      0.060834      0.060834
    01-Dec-1924      0.045108    0.0070319      0.038076      0.038076

tail(CMTT)

       Time         Return        DivYld        CapGain     CapGainA 
    ___________    _________    ___________    _________    _________

    01-May-1924    0.0074662    -4.9042e-05    0.0075152    0.0075152
    01-Jun-1924     0.017044     0.00019971     0.016844     0.016844
    01-Jul-1924     0.016657     0.00028124     0.016376     0.016376
    01-Aug-1924    0.0096193     0.00019693    0.0094224    0.0094224
    01-Sep-1924    0.0035508     0.00014389    0.0034069    0.0034069
    01-Oct-1924    0.0064063     7.9476e-05    0.0063268    0.0063268
    01-Nov-1924     0.013666     7.2083e-05     0.013594     0.013594
    01-Dec-1924     0.015515     0.00010861     0.015407     0.015407

Because the data is disaggregated, the outputs of the daily data have more rows than from the quarterly data. The filter results of the daily inputs are equal among the corresponding outputs, but bkfilter returns tables of results, instead of timetables, when you supply data in a table.

Set Filter Parameters for Data Periodicity

Load the Nelson-Plosser macroeconomic data set Data_NelsonPlosser.mat, which contains series measured yearly in the timetable DataTimeTable.

load Data_NelsonPlosser

Apply the Baxter-King filter to the real and nominal GNP series, GNPR and GNPN, respectively. Filter out cyclical component frequencies outside the interval [2,8], and set the lag length of the moving average to 3 years. Plot the trend component with each series.

bkfilter(DataTimeTable,DataVariables=["GNPR" "GNPN"], ...
    LowerCutoff=2,UpperCutoff=8,LagLength=3);

Experiment with filter parameter values by adjusting the interactive controls.

varnames = string(DataTimeTable.Properties.VariableNames);
lc = 2; % LowerCutoff
uc = 8; % UpperCutoff
q = 3; % LagLength
tfs = false; % Stationarity
vn = varnames(1); % DataVariables

figure
[TTbl,CTbl,h] = bkfilter(DataTimeTable,DataVariables=vn, ...
    LowerCutoff=lc,UpperCutoff=uc,LagLength=q,Stationarity=tfs);

Input Arguments

Y — Time series data

numeric matrix

Time series data, specified as a numObs-by-numVars numeric matrix. Each column of Y corresponds to a variable, and each row corresponds to an observation.

Data Types: double

Tbl — Time series data

table | timetable

Time series data, specified as a table or timetable with numObs rows. Each row of Tbl is an observation.

Specify numVars variables to filter by using the DataVariables argument. The selected variables must be numeric.

ax — Axes on which to plot

Axes object

Axes on which to plot, specified as an Axes object.

By default, bkfilter plots to the current axes (gca).

Note

bkfilter removes, from the specified data, all rows containing at least one missing observation, represented by a NaN value.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: bkfilter(Tbl,Stationarity=true,DataVariables=1:5) applies the Baxter-King filter to the first five variables in the input table Tbl and specifies at all input series are stationary.

LowerCutoff — Lower cutoff period for cyclical component

6 (default) | numeric scalar | numeric vector

Lower cutoff period for the cyclical component, in units of data periodicity, specified as a numeric scalar or a length numVars vector with elements greater than or equal to 2.

For a scalar, bkfilter uses LowerCutoff for all input series.

For a vector, bkfilter applies LowerCutoff(j) to selected j in the input data.

The default is 6, meaning 6 quarters (18 months), which is based on the definition of business cycle in [2].

For more details, see Tips

Example: LowerCutoff=[4 6] applies a lower cutoff of 4 to the first series in the input data and a lower cutoff of 6 to the second series.

Data Types: double

UpperCutoff — Upper cutoff period for cyclical component

32 (default) | numeric scalar | numeric vector

Upper cutoff period for the cyclical component, in units of data periodicity, specified as a numeric scalar or a length numVars vector with elements greater than or equal to the corresponding LowerCutoff for each series.

For a scalar, bkfilter uses UpperCutoff for all input series.

For a vector, bkfilter applies UpperCutoff(j) to series j in the input data.

The default is 32, meaning 32 quarters (8 years), which is based on the definition of business cycle in [2].

For more details, see Tips

Example: UpperCutoff=[32 36] applies an upper cutoff of 32 to the first series in the input data and an upper cutoff of 36 to the second series.

Data Types: double

LagLength — Number of consecutive lags

12 (default) | positive integer | vector of positive integers

Number of lags of the symmetric moving average, specified as a positive integer less than (numObs−1)/2 or vector of such positive integers.

For a scalar, bkfilter applies LagLength to all input series.

For a vector, bkfilter applies LagLength(j) to series j in the input data.

The default is 12, suggested in [1] for quarterly data.

For more details, see Tips

Example: LagLength=[4 8] specifies 4 lags for the symmetric moving average of the first series in the input data and 8 for the symmetric moving average of the second series.

Data Types: double

Stationarity — Flag indicating whether input series is stationary

false (default) | true | logical vector

Flag indicating whether input series is stationary, specified as a value or a vector of values in this table.

Value	Description
false	Input series is nonstationary
true	Input series is stationary

For a scalar, bkfilter applies Stationarity to all input series.

For a vector, bkfilter applies Stationarity(j) to series j in the input data.

Example: Stationarity=[true false] specifies that the first input series is stationary and the second input series is nonstationary.

Data Types: logical

DataVariables — Variables in Tbl

all variables (default) | string vector | cell vector of character vectors | vector of integers | logical vector

Variables in Tbl that bkfilter filters, specified as a string vector or cell vector of character vectors containing variable names in Tbl.Properties.VariableNames, or an integer or logical vector representing the indices of names. The selected variables must be numeric.

Example: DataVariables=["GDP" "CPI"]

Example: DataVariables=[true true false false] or DataVariables=[1 2] selects the first and second table variables.

Data Types: double | logical | char | cell | string

Output Arguments

Trend — Smoothed trend component τ_t

numeric vector | numeric matrix

Smoothed trend component τ_t of each series in the data, returned as a numObs-by-numVars numeric matrix. bkfilter returns Trend when you supply the input Y.

The first and last LagLength values are NaN.

Cyclical — Cyclical component c_t

table | timetable

Cyclical component c_t of each series in the data, returned as a numObs-by-numVars numeric matrix. bkfilter returns Cyclical when you supply the input Y.

The first and last LagLength values are NaN.

TTbl — Smoothed trend component τ_t

table | timetable

Smoothed trend component τ_t of each specified series, returned as a numObs-by-numVars table or timetable, the same data type as Tbl. bkfilter returns TTbl when you supply the input Tbl.

For each selected series and corresponding LagLength, the first and last LagLength values are NaN.

CTbl — Cyclical component c_t

numeric vector | numeric matrix

Cyclical component c_t of each specified series, returned as a numObs-by-numVars table or timetable, the same data type as Tbl. bkfilter returns CTbl when you supply the input Tbl.

For each selected series and corresponding LagLength, the first and last LagLength values are NaN.

h — Handles to plotted graphics objects

vector of graphics objects

Handles to plotted graphics objects, returned as a vector of graphics objects. bkfilter plots the data and trend only when you return no outputs or you return h.

h contains unique plot identifiers, which you can use to query or modify properties of the plot.

More About

Baxter-King Filter

The Baxter-King filter separates a time series y_t into a trend component τ_t (Trend and TTbl) and cyclical component c_t (Cyclical and CTbl) such that y_t = τ_t + c_t.

The method implements a symmetric, fixed-length, time-invariant moving average for the cycle as a finite-sample approximation of an ideal bandpass filter [1].

Tips

Baxter and King [1] suggest values in the table for the cutoff period name-value arguments LowerCutoff and UpperCutoff, and lag length name-value argument LagLength that depend on the periodicity of the data.

Periodicity	LowerCutoff	UpperCutoff	LagLength
Yearly	2	8	3
Quarterly	6	32	12
Monthly	18	96	36

In practice, use vectors of cutoff periods and lag lengths to test alternatives. Use the plot produced by bkfilter to compare results among settings.

References

[1] Baxter, Marianne, and Robert G. King. "Measuring Business Cycles: Approximate Band-Pass Filters for Economic Time Series." Review of Economics and Statistics 81, no. 4 (November 1999): 575–93. https://doi.org/10.1162/003465399558454.

[2] Burns, Arthur F., and Wesley C. Mitchell. Measuring Business Cycles. Cambridge, MA: National Bureau of Economic Research, 1946.

Version History

Introduced in R2023a