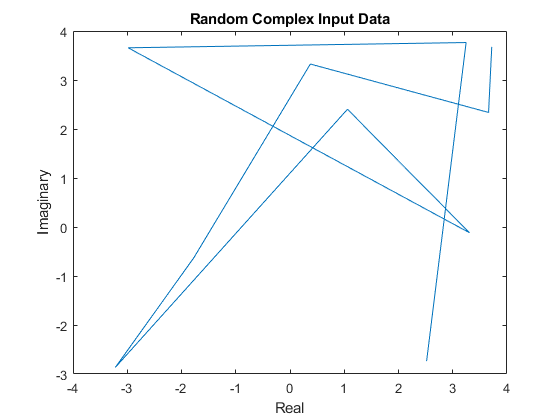
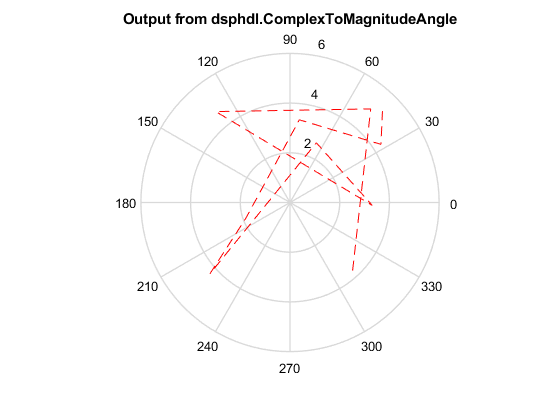
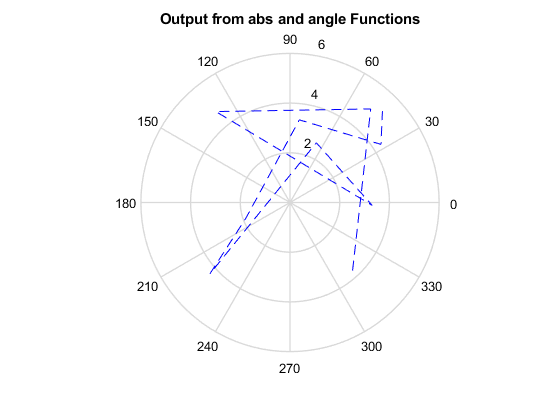
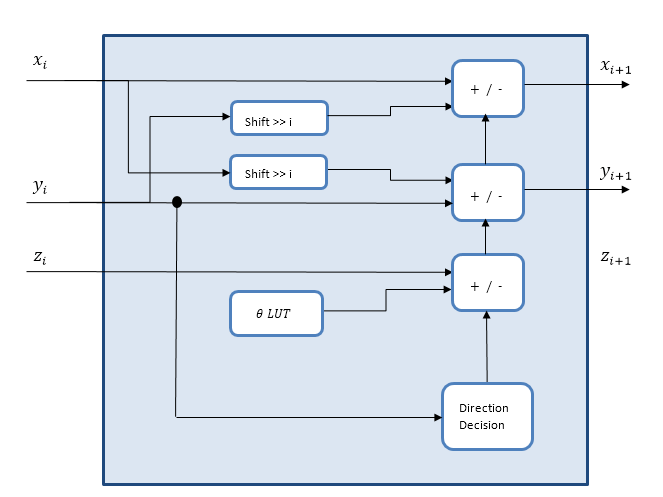
dsphdl.ComplexToMagnitudeAngle
Magnitude and phase angle of complex signal
Description
The dsphdl.ComplexToMagnitudeAngle
System object™ computes the magnitude and phase angle of a complex signal. It provides
hardware-friendly control signals. The System object uses a pipelined coordinate rotation digital computer (CORDIC) algorithm to
achieve an HDL-optimized implementation.
To compute the magnitude and phase angle of a complex signal:
Create the
dsphdl.ComplexToMagnitudeAngleobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a MATLAB® script, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the System object.
Creation
Syntax
Description
magAngle = dsphdl.ComplexToMagnitudeAngledsphdl.ComplexToMagnitudeAngle
System object, magAngle, that computes the magnitude and phase angle
of a complex input signal.
magAngle = dsphdl.ComplexToMagnitudeAngle(Name=Value)magAngle object using one or more name-value
arguments.
Example: magAngle =
dsphdl.ComplexToMagnitudeAngle(AngleFormat='Radians')
Properties
Usage
Syntax
Description
[
returns only the component magnitudes of mag,validOut]
= magAngle(X,validIn)X.
To use this syntax, set OutputFormat to
'Magnitude'.
Example: magAngle =
dsphdl.ComplextoMagnitudeAngle(OutputFormat='Magnitude');
[
returns only the component phase angles of angle,validOut]
= magAngle(X,validIn)X.
To use this syntax, set OutputFormat to
'Angle'.
Example: magAngle =
dsphdl.ComplextoMagnitudeAngle(OutputFormat='Angle');
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)