fdesign
Filter design specification object
Syntax
Description
Use the fdesign function to create a filter design
specification object that contains the specifications for a filter, such as passband ripple,
stopband attenuation, and filter order. Then, use the design function to design the filter from the filter design specifications
object. For an example, see Design of Lowpass Decimator.
Here is the workflow diagram that shows the simple procedure to design, analyze, and finally apply the filter on streaming data.

For more control options, see Filter Design Procedure. For a complete workflow, see Design a Filter in Fdesign — Process Overview.
designSpecs = fdesign.responseresponse
designSpecs = fdesign.response(spec)fdesign
object.
designSpecs = fdesign.response(___,Fs)
designSpecs = fdesign.response(___,magunits)
Examples
Design a 100-tap FIR lowpass decimator filter that reduces the sample rate of a signal from 60 kHz to 20 kHz. The passband of the filter extends up to 6 kHz. Specify a passband ripple of 0.01 dB and a stopband attenuation of 100 dB.
Fs = 60e3; N = 99; Fpass = 6e3; Apass = 0.01; Astop = 100; M = Fs/20e3;
Setup the filter design specifications object using the fdesign.decimator function.
filtSpecs = fdesign.decimator(M,'lowpass','N,Fp,Ap,Ast',N,Fpass,Apass,Astop,Fs);
Design the FIR lowpass decimator using the design function.
The resulting filter is a dsp.FIRDecimator System object™. For details on how to apply this filter to streaming data, refer to dsp.FIRDecimator.
decimFIR = design(filtSpecs,'SystemObject',true)decimFIR =
dsp.FIRDecimator with properties:
Main
DecimationFactor: 3
NumeratorSource: 'Property'
Numerator: [-1.5100e-05 -2.2164e-05 -9.6058e-06 4.3636e-05 1.3739e-04 2.3440e-04 2.6375e-04 1.5609e-04 -9.9524e-05 -4.1180e-04 -5.9905e-04 -4.7613e-04 1.3485e-05 6.9877e-04 0.0012 0.0011 2.8750e-04 -0.0010 -0.0021 -0.0022 … ] (1×100 double)
Structure: 'Direct form'
Show all properties
Use info to display information about the filter.
info(decimFIR)
ans = 10×56 char array
'Discrete-Time FIR Multirate Filter (real) '
'----------------------------------------- '
'Filter Structure : Direct-Form FIR Polyphase Decimator'
'Decimation Factor : 3 '
'Polyphase Length : 34 '
'Filter Length : 100 '
'Stable : Yes '
'Linear Phase : Yes (Type 2) '
' '
'Arithmetic : double '
Visualize the frequency response of the filter.
freqz(decimFIR,[],Fs)

Design a lowpass filter to use on a signal sampled at 96 kHz. The passband of the filter extends up to 20 kHz. The stopband of the filter starts at 24 kHz. Specify a passband ripple of 0.01 dB and a stopband attenuation of 80 dB. Determine automatically the order required to meet the specifications.
Set up the filter design specifications object using the fdesign.lowpass function.
Fs = 96e3; Fpass = 20e3; Fstop = 24e3; Apass = 0.01; Astop = 80; filtSpecs = fdesign.lowpass(Fpass,Fstop,Apass,Astop,Fs);
Determine the available design algorithms using the designmethods function.
designmethods(filtSpecs,SystemObject=true)
Design Methods that support System objects for class fdesign.lowpass (Fp,Fst,Ap,Ast): butter cheby1 cheby2 ellip equiripple ifir kaiserwin multistage
Using the design function, design an equiripple FIR filter and an elliptic IIR filter that meet the specifications.
lpFIR = design(filtSpecs,'equiripple',SystemObject=true)lpFIR =
dsp.FIRFilter with properties:
Structure: 'Direct form'
NumeratorSource: 'Property'
Numerator: [1.0908e-04 2.1016e-05 -2.3369e-04 -2.8798e-04 9.0899e-05 3.6470e-04 -5.3240e-05 -5.8338e-04 -1.6344e-04 7.4544e-04 4.8812e-04 -8.4772e-04 -9.5828e-04 7.9705e-04 0.0015 -5.2252e-04 -0.0022 -4.9607e-05 0.0028 … ] (1×101 double)
InitialConditions: 0
Show all properties
lpIIR = design(filtSpecs,'ellip',SystemObject=true)lpIIR =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [5×3 double]
Denominator: [5×3 double]
HasScaleValues: true
ScaleValues: [0.8017 0.7532 0.7030 1.2976 0.0087 1]
Show all properties
You can also measure the designs to verify that the filters satisfy the constraints.
FIRmeas = measure(lpFIR)
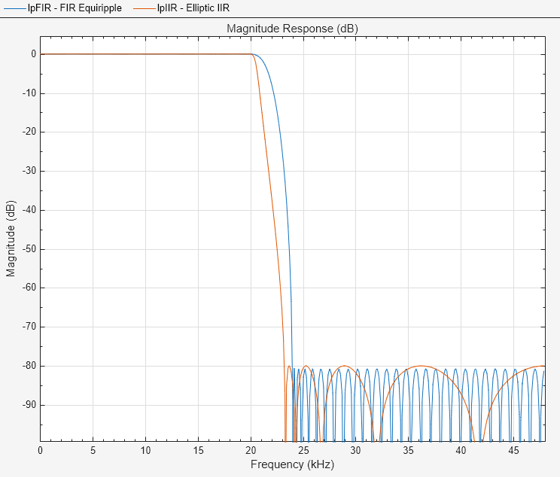
FIRmeas = Sample Rate : 96 kHz Passband Edge : 20 kHz 3-dB Point : 21.4297 kHz 6-dB Point : 21.8447 kHz Stopband Edge : 24 kHz Passband Ripple : 0.0092309 dB Stopband Atten. : 80.6014 dB Transition Width : 4 kHz
IIRmeas = measure(lpIIR)
IIRmeas = Sample Rate : 96 kHz Passband Edge : 20 kHz 3-dB Point : 20.5524 kHz 6-dB Point : 20.7138 kHz Stopband Edge : 24 kHz Passband Ripple : 0.01 dB Stopband Atten. : 80 dB Transition Width : 4 kHz
Estimate and display the computational cost of each filter. The equiripple FIR filter requires many more coefficients than the elliptic IIR filter.
FIRcost = cost(lpFIR)
FIRcost = struct with fields:
NumCoefficients: 101
NumStates: 100
MultiplicationsPerInputSample: 101
AdditionsPerInputSample: 100
IIRcost = cost(lpIIR)
IIRcost = struct with fields:
NumCoefficients: 20
NumStates: 10
MultiplicationsPerInputSample: 20
AdditionsPerInputSample: 20
Use filterAnalyzer function to visualize the resulting designs and compare their properties.
hvft = filterAnalyzer(lpFIR,lpIIR,SampleRates=Fs); setLegendStrings(hvft,["FIR Equiripple","Elliptic IIR"])
Design a lowpass Butterworth filter that has a passband edge frequency of rad/sample, a stopband frequency of rad/sample, a passband ripple of 1 dB, and a stopband attenuation of 80 dB.
Create a lowpass filter design specification object using the fdesign.lowpass function. Specify the design parameters.
lowpassSpecs = fdesign.lowpass(0.4,0.5,1,80);
To view a list of design methods available for the specification object, use the designmethods function. If multiple methods are available, pick one that best meets the design criteria. For this example, pick 'butter'.
designmethods(lowpassSpecs,SystemObject=true)
Design Methods that support System objects for class fdesign.lowpass (Fp,Fst,Ap,Ast): butter cheby1 cheby2 ellip equiripple ifir kaiserwin multistage
Furthermore, you can specify the design options used in designing the filter. To see a list of available options, run the designoptions function on lowpassSpecs. The design options are dependent on the design method you pick. The design method, in this case, 'butter', must be specified as an argument to the designoptions function.
designoptions(lowpassSpecs,"butter",Systemobject=true)ans = struct with fields:
FilterStructure: {'df1sos' 'df2sos' 'df1tsos' 'df2tsos' 'cascadeallpass' 'cascadewdfallpass'}
SOSScaleNorm: 'ustring'
SOSScaleOpts: 'fdopts.sosscaling'
MatchExactly: {'passband' 'stopband'}
DefaultFilterStructure: 'df2sos'
DefaultMatchExactly: 'stopband'
DefaultSOSScaleNorm: ''
DefaultSOSScaleOpts: [1×1 fdopts.sosscaling]
The filter order necessary to meet a set of design constraints must also be rounded up to an integer value. This loosens some of the constraints, and as a consequence, some design specifications are met while others are exceeded. The 'MatchExactly' option allows you to match the passband or stopband exactly while exceeding the specification for the other band. Design the filter so that it matches the passband exactly.
The resulting filter is a dsp.SOSFiter System object™. For details on how to apply this filter on streaming data, refer to dsp.SOSFilter.
IIRbutter = design(lowpassSpecs,"butter",MatchExactly="passband", ... SystemObject=true)
IIRbutter =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [16×3 double]
Denominator: [16×3 double]
HasScaleValues: true
ScaleValues: [0.3390 0.3104 0.2866 0.2667 0.2500 0.2359 0.2241 0.2142 0.2059 0.1990 0.1935 0.1891 0.1858 0.1834 0.1820 0.4261 1]
Show all properties
Visualize the magnitude response of the filter.
filterAnalyzer(IIRbutter)

Input Arguments
The table specifies the possible filter responses.
fdesign Response Method | Description |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Use the doc fdesign.response syntax at
the MATLAB prompt to get help on a specific structure. For example, this command
provides more information about the lowpass specification object:
doc fdesign.lowpass
Each response has a Specification property
that defines the specifications to use to design your filter. You can use defaults or
specify the Specification property when you construct the
specifications object.
Using the Specification property, you can provide filter
constraints such as the filter order or the passband attenuation to use when you
construct your filter from the specification object.
Filter design specifications, specified as a character vector. The set of available
specification options depends on the
fdesign. function. For more
information, refer to the individual
responsefdesign. pages.response
The filter design is based on the specifications provided by the
fdesign. object. For
example, when you create a default lowpass filter design specification object,
responsefdesign.lowpass, the specification expression is set to
'Fp,Fst,Ap,Ast'. The filter design parameters —
Fp (passband frequency), Fst (stopband
frequency), Ap (passband ripple), and Ast
(stopband attenuation) — are set to default values. The design function designs the filter based on these parameters.
Specifications that do not contain the filter order result in minimum-order designs
when you invoke the design
function:
d = fdesign.lowpass; % Specification is 'Fp,Fst,Ap,Ast' FIReq = design(d,'equiripple','SystemObject',true); length(FIReq.Numerator) % Returns 43. The filter order is 42
The specification option you choose determines which design methods are applicable.
You can use the setspecs function to set all of the
specifications simultaneously.
You can set filter specification values by passing them after the
Specification argument, or by passing the values without the
Specification.
Filter object constructors take the input arguments in the same order as setspecs and Specification.
When the first input to
fdesign. is not a valid
responseSpecification option, fdesign assumes that
the input argument is a filter specification and applies it using the default
Specification option. For example,
'Fp,Fst,Ap,Ast' is the default for a lowpass object.
Sample rate to use in filter specifications, specified in Hz. The sample rate scalar must be the last input argument. If you specify a sample rate, all frequency specifications are in Hz.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Units for magnitude specification, specified as:
'dB'–– decibels'linear'–– linear units'squared'–– power units
When you omit the magunits argument, fdesign
assumes that all magnitudes are in dB. Note that fdesign stores all
magnitude specifications in dB. If you set magunits to an option
other than 'dB', the function converts the unit to
'dB'.
Output Arguments
fdesign returns a filter design specification object. Every
filter design specification object has these properties:
Property Name | Default Value | Description |
|---|---|---|
| Depends on the chosen type | Defines the type of filter to design, such as an interpolator or bandpass filter. This is a read-only value. |
| Depends on the chosen type | Defines the filter characteristics used to define the desired filter
performance, such as the cutoff frequency |
| Depends on the filter type you choose | Contains descriptions of the filter specifications used to define the object, and the filter specifications you use when you create a filter from the object. This is a read-only value. |
| Logical | Determines whether the filter calculation uses a normalized frequency
from 0 to 1, or the frequency band from 0 to Fs/2, the sampling frequency. Accepts either
|
In addition to these properties, filter design specification objects can have other properties as well, depending on whether they design single-rate filters or multirate filters.
Added Properties for Multirate Filters | Description |
|---|---|
| Specifies the amount to decrease the sampling rate. Always a positive integer. |
| Specifies the amount to increase the sampling rate. Always a positive integer. |
| Polyphase length is the length of each polyphase subfilter that
composes the decimator or interpolator or rate-change factor filters. Total
filter length is the product of |
More About
Here is the workflow diagram of the overall procedure for designing and analyzing the filter.

Here are the steps in detail:
Create an
fdesign.specification object to specify the design parameters.responseUse
designmethodsto determine the filter design methods that work for your new filter specification object. If you choose to use the default design method, then this step is optional.If you prefer to change the design options and would like to see a list of available options, run the
designoptionsfunction on the specification object. The output also shows the design options the filter uses by default.Use
designto design the filter from the filter specification object. Specify the design method (determined from step 2) as an input. If the design options must change from the default values, specify them as name-value pairs following the design method.Further analysis, such as viewing the frequency response of the filter, computing the cost of implementing the filter, and measuring the filter response characteristics, can be done using one of the supported Analysis Functions for Filter System Objects.
Once you analyze the filter and determine that the filter satisfies the design constraints, you can apply the filter object to streaming input data. For details on how to pass data to the filter object, refer to the corresponding filter System object™ reference pages.
For a detailed example on the design and analysis, see Lowpass Butterworth Filter Specification and Design.
Version History
Introduced in R2009a
See Also
Apps
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)