visualize
Visualize frequency response of individual filter stages or sum of filter paths between input and output channels
Since R2024b
Description
visualize( visualizes the frequency
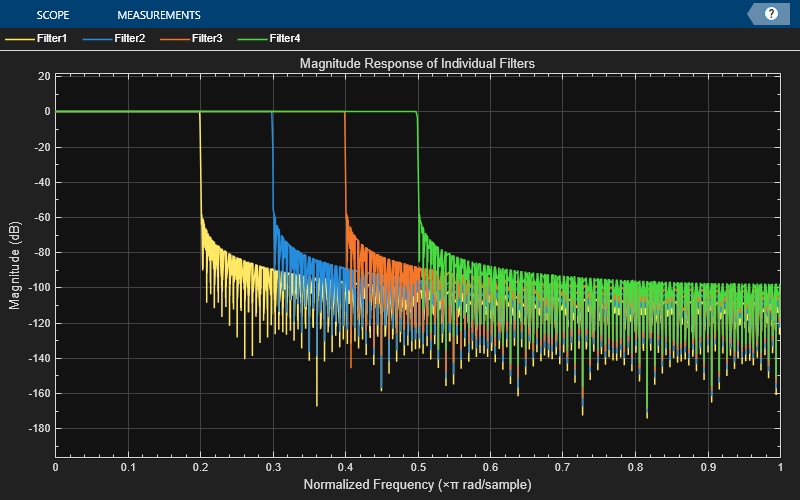
response of the individual filters of the input filter object.filtObj)
visualize(___,
visualizes the frequency response of the filter with additional properties specified by one
or more name-value arguments.Name=Value)
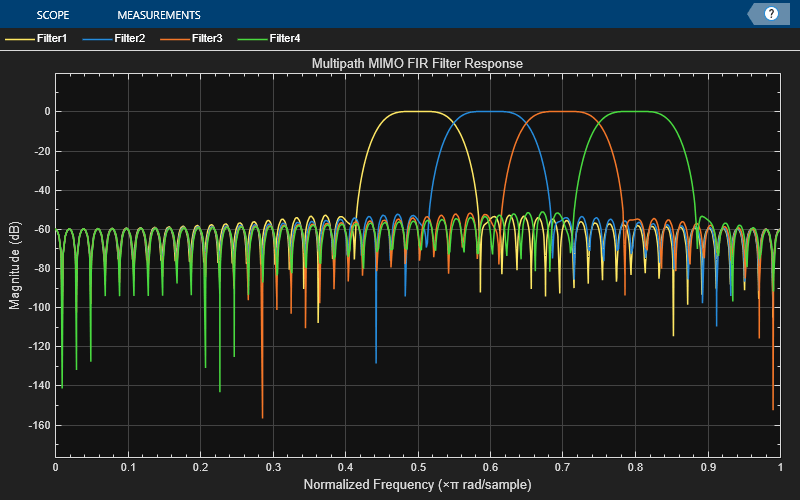
For example, to visualize the frequency response of the sum of all filter paths between
each input and output channel, set SumFilterPaths to
true.
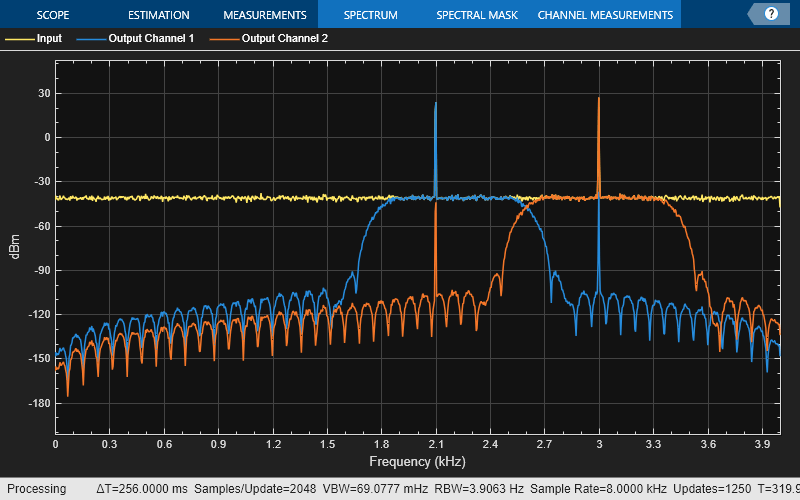
Example: visualize(filtobj,SumFilterPaths=true,NumInputChannels=2)
DFV = visualize(___)dsp.DynamicFilterVisualizer object which contains the settings to customize the
filter visualization.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Version History
Introduced in R2024b