dsp.FarrowRateConverter
Polynomial sample rate converter with arbitrary conversion factor
Description
The dsp.FarrowRateConverter
System object™ implements a polynomial-fit sample rate conversion filter using a Farrow
structure. You can use this object to convert the sample rate of a signal up or down by an
arbitrary factor. This object supports fixed-point operations.
To convert the sample rate of a signal:
Create the
dsp.FarrowRateConverterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
frc = dsp.FarrowRateConverterfrc. For each channel of an input signal,
frc converts the input sample rate to the output sample
rate.
frc = dsp.FarrowRateConverter(Name=Value)InputSampleRate to 45200.
Example: frc =
dsp.FarrowRateConverter(Specification="Coefficients",Coefficients=[1
2; 3 4]) returns a filter that converts from 44.1 kHz to
48 kHz using custom coefficients that implement a 2nd-order polynomial
filter.
frc = dsp.FarrowRateConverter(fsIn,fsOut,tol,np)frc, with InputSampleRate property set
to fsIn, OutputSampleRate property set
to fsOut, OutputRateTolerance
property set to tol, and PolynomialOrder property set
to np.
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
Algorithms
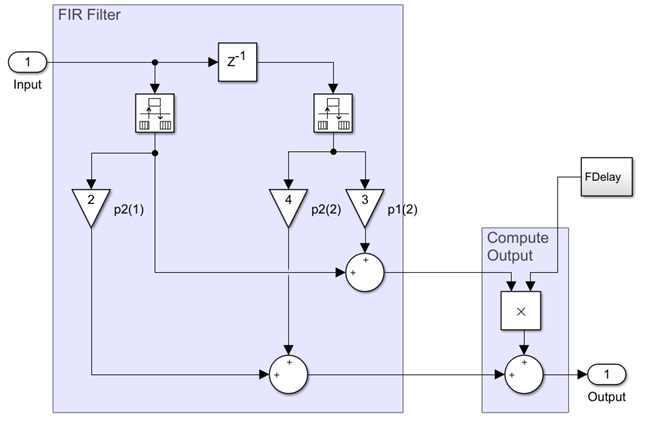
Farrow filters implement piecewise polynomial interpolation using Horner’s rule to compute samples from the polynomial. The polynomial coefficients used to fit the input samples correspond to the Lagrange interpolation coefficients.
Once a polynomial is fitted to the input data, the value of the polynomial can be calculated at any point. Therefore, a polynomial filter enables interpolation at arbitrary locations between input samples.
You can use a polynomial of any order to fit to the existing samples. However, since large-order polynomials frequently oscillate, polynomials of order 1, 2, 3, or 4 are used in practice.
The algorithm computes interpolated values at the desired locations by varying only the fractional delay µ. This value is the interval between the previous input sample and the current output sample. All filter coefficients remain constant.
The input samples are filtered using M + 1 FIR filters, where M is the polynomial order.
The outputs of these filters are multiplied by the fractional delay, µ.
The output is the sum of the multiplication results.
Here is the filter structure diagram of the Farrow filter with a polynomial order of 4.

References
[1] Hentschel, T., and G. Fettweis. "Continuous-Time Digital Filters for Sample-Rate Conversion in Reconfigurable Radio Terminals." Frequenz. Vol. 55, Number 5-6, 2001, pp. 185–188.
Extended Capabilities
Version History
Introduced in R2014bSee Also
Functions
getPolynomialCoefficients|getActualOutputRate|getRateChangeFactors|freqz|freqzmr|filterAnalyzer|info|cost|outputDelay