dsp.CICInterpolator
Interpolate signal using cascaded integrator-comb filter
Description
The dsp.CICInterpolator
System object™ interpolates an input signal using a cascaded integrator-comb (CIC)
interpolation filter. The CIC interpolation filter structure consists of N
sections of cascaded comb filters, followed by a rate change by a factor of
R, followed by N sections of cascaded integrators. For
details, see Algorithms. The NumSections property specifies N, the number of sections in
the CIC filter. The InterpolationFactor property
specifies R, the interpolation factor. The getFixedPointInfo
function returns the word lengths and fraction lengths of the fixed-point sections and the
output for the dsp.CICInterpolator
System object.
Note
This object requires a Fixed-Point Designer™ license.
To interpolate a signal using a CIC filter:
Create the
dsp.CICInterpolatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
cicInterp = dsp.CICInterpolator
cicInterp = dsp.CICInterpolator(R,M,N)InterpolationFactor
property set to R, the DifferentialDelay
property set to M, and the NumSections property
set to N.
cicInterp = dsp.CICInterpolator(Name=Value)InterpolationFactor to 4.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Factor by which the input signal is interpolated, specified as a positive integer.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Differential delay value used in each of the comb sections of the filter, specified
as a positive integer. For details, see Algorithms. If the
differential delay is of built-in integer class data type, the interpolation factor must
be the same integer data type or double. For example, if the
differential delay is an int8, then the interpolation factor must be
an int8 or double.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Number of integrator and comb sections of the CIC filter, specified as a positive integer. This number indicates the number of sections in either the comb part or the integrator part of the filter. The total number of sections in the CIC filter is twice the number of sections given by this property.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Fixed-point property designations, specified as one of the following:
Full precision– The word length and fraction length of the CIC filter sections and the object output operate in full precision.Minimum section word lengths– Specify the output word length through the OutputWordLength property. The object determines the filter section data type and the output fraction length that give the best possible precision. For details, seegetFixedPointInfoandcicInterpOutargument.Specify word lengths– Specify the word lengths of the CIC filter sections and the object output through the SectionWordLengths and OutputWordLength properties. The object determines the corresponding fraction lengths to give the best possible precision. For details, seegetFixedPointInfoand thecicInterpOutargument.Specify word and fraction lengths– Specify the word length and fraction length of the CIC filter sections and the object output through the SectionWordLengths, SectionFractionLengths, OutputWordLength, and OutputFractionLength properties.
Fixed-point word lengths to use for each filter section, specified as a scalar or a
row vector of integers. The word length must be greater than or equal to 2. If you
specify a scalar, the value applies to all the sections of the filter. If you specify a
vector, the vector must be of length 2 × NumSections.
Example: 32
Example: [32 32 32 32]
Dependencies
This property applies when you set the
FixedPointDataType property to
"Specify word lengths" or "Specify
word and fraction lengths".
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Fixed-point fraction lengths to use for each filter section, specified as a scalar
or a row vector of integers. The fraction length can be negative, 0, or positive. If you
specify a scalar, the value applies to all the sections of the filter. If you specify a
vector, the vector must be of length 2 × NumSections.
Example: -2
Example: [-2 0 5 8]
Dependencies
This property applies when you set the
FixedPointDataType property to
"Specify word and fraction lengths".
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Fixed-point word length to use for the filter output, specified as a scalar integer greater than or equal to 2.
Dependencies
This property applies when you set the
FixedPointDataType property to one of
"Minimum section word lengths",
"Specify word lengths", or "Specify
word and fraction lengths".
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Fixed-point fraction length to use for the filter output, specified as a scalar integer.
Dependencies
This property applies when you set the
FixedPointDataType property to
"Specify word and fraction lengths".
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Usage
Description
cicInterpOut = cicInterp(input)
Input Arguments
Data input, specified as a vector or matrix. If the input is of single or double data type, property settings related to the fixed-point data types are ignored.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Complex Number Support: Yes
Output Arguments
Interpolated output, returned as a vector or a matrix. The output frame size
equals (InterpolationFactor) × input frame size. The
complexity of the output data matches that of the input data. If the input is
single or double, the output data type matches
the input data type.
If the input is of built-in integer data type or of fixed-point data type, the output word length and fraction length depend on the fixed-point data type setting you choose through the FixedPointDataType property.
Full precision
When the FixedPointDataType property is
set to "Full precision", the following
relationship applies:
where,
WLoutput –– Word length of the output data.
FLoutput –– Fraction length of the output data.
WLinput –– Word length of the input data.
FLinput –– Fraction length of the input data.
NumSect –– Number of sections in the CIC filter specified through the NumSections property.
WLinput and FLinput are inherited from the data input you pass to the object algorithm. For built-in integer inputs, the fraction length is 0.
Minimum section word lengths
When the FixedPointDataType property is
set to "Minimum section word lengths", the
output word length is the value you specify in OutputWordLength property. The
output fraction length,
FLoutput is given by
the following equation:
Specify word and fraction lengths
When the FixedPointDataType is set to
"Specify word and fraction lengths", the
output word length and fraction length are the values you specify
in the OutputWordLength and OutputFractionLength
properties.
Specify word lengths
When the FixedPointDataType is set to
"Specify word lengths", the output word
length is the value you specify in the
OutputWordLength property. The output
fraction length,
FLoutput is given by
the following equation:
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Complex Number Support: Yes
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
impz | Impulse response of discrete-time filter System object |
freqz | Frequency response of discrete-time filter System object |
freqzmr | Compute DTFT approximation of impulse response of multirate or single-rate filter |
phasez | Phase response of discrete-time filter System object (unwrapped) |
filterAnalyzer | Analyze filters with Filter Analyzer app |
gain | Gain of CIC filter System object |
getFixedPointInfo | Get fixed-point word and fraction lengths |
info | Information about filter System object |
outputDelay | Determine output delay of single-rate or multirate filter |
For a list of filter analysis methods this object supports, type
dsp.CICInterpolator.helpFilterAnalysis in the MATLAB® command prompt. For the corresponding function reference pages, see Analysis Functions for Filter System Objects.
Examples
Create a dsp.CICInterpolator System object™ with InterpolationFactor set to 2. Interpolate a fixed-point signal by a factor of 2 from 22.05 kHz to 44.1 kHz.
cicint = dsp.CICInterpolator(2)
cicint =
dsp.CICInterpolator with properties:
InterpolationFactor: 2
DifferentialDelay: 1
NumSections: 2
FixedPointDataType: 'Full precision'
Create a dsp.SineWave object with SampleRate set to 22.05 kHz, SamplesPerFrame set to 32, and OutputDataType set to "Custom". To generate a fixed-point signal, set the CustomOutputDataType property to a numerictype object. For the purpose of this example, set the value to numerictype([],16). The fraction length is computed based on the values of the generated sinusoidal signal to give the best possible precision.
To generate a fixed-point signal, set the Method property of the dsp.SineWave object to "Table lookup". This method of generating the sinusoidal signal requires that the period of every sinusoid in the output be evenly divisible by the sample period. That is, must be an integer value for every channel i = 1, 2, ..., N. The value of equals , the variable is the frequency of the sinusoidal signal, and is the sample rate of the signal. In other words, the ratio must be an integer. For more details, see the Algorithms section on the dsp.SineWave object page.
In this example, is set to 22050 Hz and is set to 1050 Hz.
Fs = 22.05e3; sine = dsp.SineWave(Frequency=1050,... SampleRate=Fs,... SamplesPerFrame=32,... Method="Table lookup",... OutputDataType="Custom")
sine =
dsp.SineWave with properties:
Amplitude: 1
Frequency: 1050
PhaseOffset: 0
ComplexOutput: false
Method: 'Table lookup'
TableOptimization: 'Speed'
SamplesPerFrame: 32
SampleRate: 22050
OutputDataType: 'Custom'
Show all properties
In each loop of the iteration, stream in a frame of the fixed-point sinusoidal signal sampled at 22.05 kHz. Interpolate the streamed signal by a factor of 2. The interpolated output has 64 samples per frame.
for i = 1:16 x = sine(); y = cicint(x); end
The output of the CIC interpolation filter is amplified by a specific gain value. You can determine this value using the gain function. This gain equals the gain of the stage of the CIC interpolation filter and equals , where is the interpolation factor, is the differential delay, and is the number of sections of the CIC interpolator.
gainCIC = gain(cicint)
gainCIC = 2
To adjust this amplified output and to match it to the amplitude of the original signal, divide the CIC interpolated signal with the computed gain value.
Compare the last frames of the original and the interpolated signals. While plotting, account for the output latency of 2 samples.
n = (0:63)'; stem(n(1:31)/Fs,double(x(1:31)),"r","filled") hold on; I = cicint.InterpolationFactor; stem(n(1:61)/(Fs*I), ... double(y(4:end))/gainCIC,"b") xlabel("Time (sec)") ylabel("Signal Amplitude") legend("Original Signal",... "Interpolated Signal",... "location","north") hold off;

Using the info function in the "long" format, obtain the word lengths and fraction lengths of the fixed-point filter sections and the filter output.
info(cicint,"long")ans = 16×61 char array
'Discrete-Time FIR Multirate Filter (real) '
'----------------------------------------- '
'Filter Structure : Cascaded Integrator-Comb Interpolator'
'Interpolation Factor : 2 '
'Differential Delay : 1 '
'Number of Sections : 2 '
'Stable : Yes '
'Linear Phase : Yes (Type 1) '
' '
' '
'Implementation Cost '
'Number of Multipliers : 0 '
'Number of Adders : 4 '
'Number of States : 4 '
'Multiplications per Input Sample : 0 '
'Additions per Input Sample : 6 '
Using the getFixedPointInfo function, you can determine the word lengths and fraction lengths of the fixed-point sections and the output of the dsp.CICDecimator and dsp.CICInterpolator System objects. The data types of the filter sections and the output depend on the FixedPointDataType property of the filter System object™.
Full precision
Create a dsp.CICDecimator object. The default value of the NumSections property is 2. This value indicates that there are two integrator and comb sections. The WLs and FLs vectors returned by the getFixedPointInfo function contain five elements each. The first two elements represent the two integrator sections. The third and fourth elements represent the two comb sections. The last element represents the filter output.
cicD = dsp.CICDecimator
cicD =
dsp.CICDecimator with properties:
DecimationFactor: 2
DifferentialDelay: 1
NumSections: 2
FixedPointDataType: 'Full precision'
By default, the FixedPointDataType property of the object is set to "Full precision". Calling the getFixedPointInfo function on this object with the input numeric type, nt, yields the following word length and fraction length vectors.
nt = numerictype(1,16,15)
nt =
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 15
[WLs,FLs] = getFixedPointInfo(cicD,nt) %#okWLs = 1×5
18 18 18 18 18
FLs = 1×5
15 15 15 15 15
For details on how the word lengths and fraction lengths are computed, see the description for Output Arguments.
If you lock the cicD object by passing an input to its algorithm, you do not need to pass the nt argument to the getFixedPointInfo function.
input = int64(randn(8,1))
input = 8×1 int64 column vector
1
2
-2
1
0
-1
0
0
output = cicD(input)
output =
0
1
3
0
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 66
FractionLength: 0
[WLs,FLs] = getFixedPointInfo(cicD) %#okWLs = 1×5
66 66 66 66 66
FLs = 1×5
0 0 0 0 0
The output and section word lengths are the sum of input word length, 64 in this case, and the number of sections, 2. The output and section fraction lengths are 0 since the input is a built-in integer.
Minimum section word lengths
Release the object and change the FixedPointDataType property to "Minimum section word lengths". Determine the section and output fixed-point information when the input is fixed-point data, fi(randn(8,2),1,24,15).
release(cicD);
cicD.FixedPointDataType = "Minimum section word lengths"cicD =
dsp.CICDecimator with properties:
DecimationFactor: 2
DifferentialDelay: 1
NumSections: 2
FixedPointDataType: 'Minimum section word lengths'
OutputWordLength: 32
inputF = fi(randn(8,2),1,24,15)
inputF =
3.5784 -0.1241
2.7694 1.4897
-1.3499 1.4090
3.0349 1.4172
0.7254 0.6715
-0.0630 -1.2075
0.7148 0.7172
-0.2050 1.6302
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 24
FractionLength: 15
[WLs, FLs] = getFixedPointInfo(cicD,numerictype(inputF)) %#okWLs = 1×5
26 26 26 26 32
FLs = 1×5
15 15 15 15 21
Specify word and fraction lengths
Change the FixedPointDataType property to "Specify word and fraction lengths". Determine the fixed-point information using the getFixedPointInfo function.
cicD.FixedPointDataType = "Specify word and fraction lengths"cicD =
dsp.CICDecimator with properties:
DecimationFactor: 2
DifferentialDelay: 1
NumSections: 2
FixedPointDataType: 'Specify word and fraction lengths'
SectionWordLengths: 16
SectionFractionLengths: 0
OutputWordLength: 32
OutputFractionLength: 0
[WLs, FLs] = getFixedPointInfo(cicD,numerictype(inputF)) %#okWLs = 1×5
16 16 16 16 32
FLs = 1×5
0 0 0 0 0
The section and output word lengths and fraction lengths are assigned as per the respective fixed-point properties of the cicD object. These values are not determined by the input numeric type. To confirm, call the getFixedPointInfo function without passing the numerictype input argument.
[WLs, FLs] = getFixedPointInfo(cicD) %#okWLs = 1×5
16 16 16 16 32
FLs = 1×5
0 0 0 0 0
Specify word lengths
To specify the word lengths of the filter section and output, set the FixedPointDataType property to "Specify word lengths".
cicD.FixedPointDataType = "Specify word lengths"cicD =
dsp.CICDecimator with properties:
DecimationFactor: 2
DifferentialDelay: 1
NumSections: 2
FixedPointDataType: 'Specify word lengths'
SectionWordLengths: 16
OutputWordLength: 32
The getFixedPointInfo function requires the input numeric type because that information is used to compute the section and word fraction lengths.
[WLs, FLs] = getFixedPointInfo(cicD,numerictype(inputF))
WLs = 1×5
16 16 16 16 32
FLs = 1×5
5 5 5 5 21
For more details on how the function computes the word and fraction lengths, see the description for Output Arguments.
More About
CIC filters are an optimized class of linear phase FIR filters composed of a comb part and an integrator part.
The CIC interpolation filter is conceptually given by an upsampler followed by a single rate CIC filter, H(z), which is a lowpass anti-imaging filter. The CIC interpolation filter increases the sample rate of an input signal by an integer factor using a cascaded integrator-comb (CIC) filter.

In a more efficient implementation, the single rate CIC filter H(z) is factorized this way:
where,
HC is the transfer function of the N sections of the cascaded comb filters, each with a width of RM.
HI is the transfer function of the integrator part of the filter containing N stages of integrators.
N is the number of sections. The number of sections in a CIC filter is defined as the number of sections in either the comb part or the integrator part of the filter. This value does not represent the total number of sections throughout the entire filter.
R is the interpolation factor.
M is the differential delay.
In the overall multirate realization, the algorithm applies the noble identity for interpolation and moves the rate change factor, R, to follow after the N sections of the cascaded comb filters.
The transfer function of the resulting filter is given by the following equation:
For a block diagram that shows the multirate implementation, see Algorithms.
The fixed-point signal diagram shows the data types that the
dsp.CICInterpolator object uses for fixed-point signals.
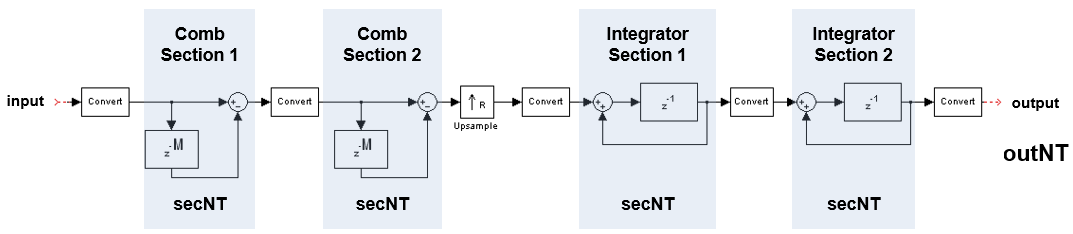
where,
secNT = numerictype(1,secWL,secFL)outNT = numertictype(1,outWL,outFL)secWL is the section word length you specify through the SectionWordLengths property.
secFL is the section fraction length you specify through the SectionFractionLengths property.
outWL is the output word length you specify through the OutputWordLength property.
outFL is the output fraction length you specify through the OutputFractionLength property.
The value of NumSections in this diagram is 2.
Algorithms
The CIC interpolation filter in More About is realized as a cascade of N sections of comb filters followed by a rate change by a factor R, followed by N sections of cascaded integrators.

This diagram shows two sections of cascaded comb filters and two sections of cascaded integrators. The unit delay in the integrator portion of the CIC filter can be located in either the feedforward or the feedback path. These two configurations yield identical filter frequency response. However, the numerical outputs from these two configurations are different due to the latency. This algorithm puts the unit delay in the feedforward path of the integrator since it is a preferred configuration for HDL implementation.
References
[1] Hogenauer, E.B. "An Economical Class of Digital Filters for Decimation and Interpolation." IEEE Transactions on Acoustics, Speech and Signal Processing. Volume 29, Number 2, 1981, 155–162.
[2] Meyer-Baese, U. Digital Signal Processing with Field Programmable Gate Arrays. New York: Springer, 2001.
[3] Harris, Fredric J. Multirate Signal Processing for Communication Systems. Indianapolis, IN: Prentice Hall PTR, 2004.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
For workflow and limitations, see HDL Code Generation for System Objects (HDL Coder).
Note
For a hardware-optimized CIC interpolator algorithm that supports HDL code generation,
use the dsphdl.CICInterpolator (DSP HDL Toolbox)
System object. This object has hardware-friendly valid and reset control signals, and
models exact hardware latency behavior. The object supports HDL code generation with
HDL Coder™ tools.
Version History
Introduced in R2012aStarting in R2025a, the Filter Design HDL Coder™ product is discontinued. So, this object no longer supports HDL code
generation by using the generatehdl function. The object still supports
code generation using HDL Coder tools.
See Also
Functions
impz|freqz|freqzmr|phasez|filterAnalyzer|gain|getFixedPointInfo|info|outputDelay
Objects
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)