dist
Angular distance in radians
Description
distance = dist(quatA,quatB)quatA and quatB.
Examples
Input Arguments
Output Arguments
Algorithms
The dist function returns the angular distance between two
quaternions.
A quaternion may be defined by an axis (ub,uc,ud) and angle of rotation θq: .
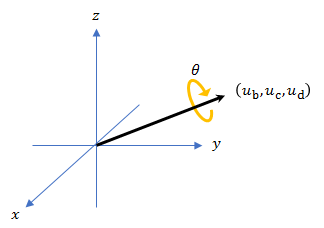
Given a quaternion in the form, , where a is the real part, you can solve for the angle of q as .
Consider two quaternions, p and q, and the product . As p approaches q, the angle of z goes to 0, and z approaches the unit quaternion.
The angular distance between two quaternions can be expressed as .
Using the quaternion data type syntax, the angular distance is
calculated
as:
angularDistance = 2*acos(abs(parts(p*conj(q))));
Extended Capabilities
Version History
Introduced in R2020a