plot
Plot receiver operating characteristic (ROC) curves and other performance curves
Since R2022b
Syntax
Description
plot( creates
a receiver operating characteristic (ROC) curve, which is a plot of the true positive
rate (TPR) versus the false positive rate (FPR), for each class in the rocObj)ClassNames property of the
rocmetrics object
rocObj. The function marks the model operating point for each
curve, and displays the value of the area under the ROC curve (AUC) and the class name for the curve in the legend.
plot(___, specifies
additional options using one or more name-value arguments in addition to any of the input
argument combinations in the previous syntaxes. For example,
Name=Value)AverageCurveType="macro",ClassNames=[] computes the average
performance metrics using the macro-averaging method and plots the average ROC curve
only.
[ also returns graphics objects for the model operating points and diagonal line.curveObj,graphicsObjs] = plot(___)
Examples
Load a sample of predicted classification scores and true labels for a classification problem.
load('flowersDataResponses.mat')trueLabels is the true labels for an image classification problem and scores is the softmax prediction scores. scores is an N-by-K array where N is the number of observations and K is the number of classes.
trueLabels = flowersData.trueLabels; scores = flowersData.scores;
Load the class names. The column order of scores follows the class order stored in classNames.
classNames = flowersData.classNames;
Create a rocmetrics object by using the true labels in trueLabels and the classification scores in scores. Specify the column order of scores using classNames.
rocObj = rocmetrics(trueLabels,scores,classNames);
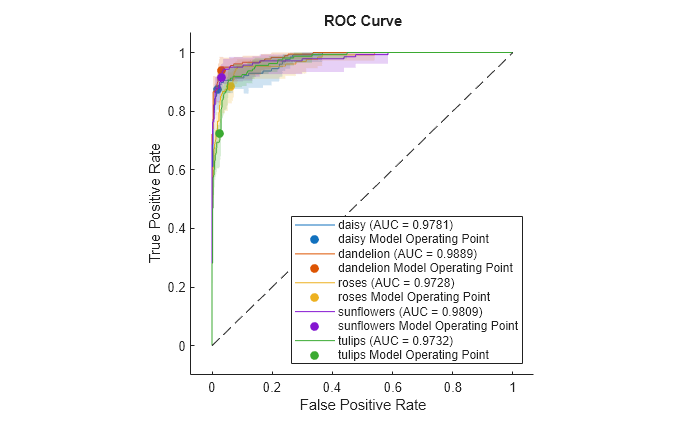
rocObj is a rocmetrics object that stores performance metrics for each class in the property. Compute the AUC for all the model classes by calling auc on the object.
a = auc(rocObj)
a = 1×5 single row vector
0.9781 0.9889 0.9728 0.9809 0.9732
Plot the ROC curve for each class. The plot function also returns the AUC values for the classes.
plot(rocObj)

The filled circle markers indicate the model operating points. The legend displays the class name and AUC value for each curve.
Plot the macro average ROC curve.
plot(rocObj,AverageCurveType=["macro"],ClassNames=[])
Create a rocmetrics object and plot performance curves by using the plot function. Specify the XAxisMetric and YAxisMetric name-value arguments of the plot function to plot different types of performance curves other than the ROC curve. If you specify new metrics when you call the plot function, the function computes the new metrics and then uses them to plot the curve.
Load a sample of true labels and the prediction scores for a classification problem. For this example, there are five classes: daisy, dandelion, roses, sunflowers, and tulips. The class names are stored in classNames. The scores are the softmax prediction scores generated using the predict function. scores is an N-by-K array where N is the number of observations and K is the number of classes. The column order of scores follows the class order stored in classNames.
load('flowersDataResponses.mat')
scores = flowersData.scores;
trueLabels = flowersData.trueLabels;
classNames = flowersData.classNames;Create a rocmetrics object. The rocmetrics function computes the FPR and TPR at different thresholds.
rocObj = rocmetrics(trueLabels,scores,classNames);
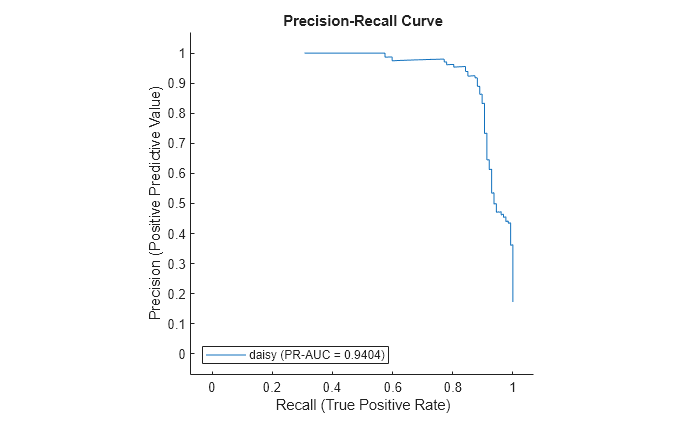
Plot the precision-recall curve for the first class. Specify the y-axis metric as precision (or positive predictive value) and the x-axis metric as recall (or true positive rate). The plot function computes the new metric values and plots the curve.
curveObj = plot(rocObj,ClassNames=classNames(1), ... YAxisMetric="PositivePredictiveValue",XAxisMetric="TruePositiveRate");
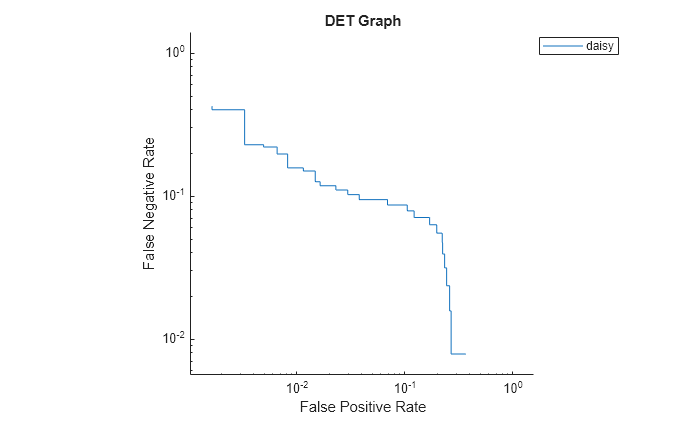
Plot the detection error tradeoff (DET) graph for the first class. Specify the y-axis metric as the false negative rate and the x-axis metric as the false positive rate. Use a log scale for the x-axis and y-axis.
f = figure; plot(rocObj,ClassNames=classNames(1), ... YAxisMetric="FalseNegativeRate",XAxisMetric="FalsePositiveRate") f.CurrentAxes.XScale = "log"; f.CurrentAxes.YScale = "log"; title("DET Graph")
Compute the confidence intervals for FPR and TPR for fixed threshold values by using bootstrap samples, and plot the confidence intervals for TPR on the ROC curve by using the plot function. This examples requires Statistics and Machine Learning Toolbox™.
Load a sample of true labels and the prediction scores for a classification problem. For this example, there are five classes: daisy, dandelion, roses, sunflowers, and tulips. The class names are stored in classNames. The scores are the softmax prediction scores generated using the predict function. scores is an N-by-K array where N is the number of observations and K is the number of classes. The column order of scores follows the class order stored in classNames.
load('flowersDataResponses.mat')
scores = flowersData.scores;
trueLabels = flowersData.trueLabels;
classNames = flowersData.classNames;Create a rocmetrics object by using the true labels in trueLabels and the classification scores in scores. Specify the column order of scores using classNames. Specify NumBootstraps as 100 to use 100 bootstrap samples to compute the confidence intervals.
rocObj = rocmetrics(trueLabels,scores,classNames,NumBootstraps=100);
Plot the ROC curve and the confidence intervals for TPR. Specify ShowConfidenceIntervals=true to show the confidence intervals.
plot(rocObj,ShowConfidenceIntervals=true)
The shaded area around each curve indicates the confidence intervals. rocmetrics computes the ROC curves using the scores. The confidence intervals represent the estimates of uncertainty for the curve.
Specify one class to plot by using the ClassNames name-value argument.
plot(rocObj,ShowConfidenceIntervals=true,ClassNames="daisy")
Input Arguments
Object evaluating classification performance, specified as a rocmetrics
object.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: plot(rocObj,YAxisMetric="PositivePredictiveValue",XAxisMetric="TruePositiveRate")
plots the precision (positive predictive value) versus the recall (true positive rate),
which represents a precision-recall curve.
Since R2024b
Method for averaging ROC or other performance curves, specified as
"none", "micro", "macro",
"weighted", a string array of method names, or a cell array of
method names.
If you specify
"none"(default), theplotfunction does not create the average performance curve.If you specify multiple methods as a string array or a cell array of character vectors, then the
plotfunction plots multiple average performance curves using the specified methods.If you specify one or more averaging methods and specify
ClassNames=[], then theplotfunction plots only the average performance curves.
plot computes the averages of performance metrics for a
multiclass classification problem, and plots the average performance curves using these
methods:
"micro"(micro-averaging) —plotfinds the average performance metrics by treating all one-versus-all binary classification problems as one binary classification problem. The function computes the confusion matrix components for the combined binary classification problem, and then computes the average metrics (as specified by theXAxisMetricandYAxisMetricname-value arguments) using the values of the confusion matrix."macro"(macro-averaging) —plotcomputes the average values for the metrics by averaging the values of all one-versus-all binary classification problems."weighted"(weighted macro-averaging) —plotcomputes the weighted average values for the metrics using the macro-averaging method and using the prior class probabilities (thePriorproperty ofrocObj) as weights.
The algorithm type determines the length of the vectors in the XData, YData, and
Thresholds
properties of a ROCCurve object, returned by plot,
for the average performance curve. For more details, see Average of Performance Metrics.
Example: AverageCurveType="macro"
Example: AverageCurveType=["micro","macro"]
Data Types: char | string | cell
Class labels to plot, specified as a categorical, character, or string array, logical or
numeric vector, or cell array of character vectors. The values and data types in
ClassNames must match those of the class names in the ClassNames property
of rocObj. (The software treats character or string arrays as cell arrays of character vectors.)
If you specify multiple class labels, the
plotfunction plots a ROC curve for each class.If you specify
ClassNames=[]and specify one or more averaging methods usingAverageCurveType, then theplotfunction plots only the average ROC curves.
Example: ClassNames=["red","blue"]
Data Types: single | double | logical | char | string | cell | categorical
Flag to show the confidence intervals of the y-axis metric
(YAxisMetric), specified as a numeric or logical
0 (false) or 1
(true).
The ShowConfidenceIntervals value can be true only if
the Metrics property of
rocObj contains the confidence intervals for the
y-axis metric.
Example: ShowConfidenceIntervals=true
Using confidence intervals requires Statistics and Machine Learning Toolbox™.
Data Types: single | double | logical
Flag to show the diagonal line that extends from [0,0] to
[1,1], specified as a numeric or logical 1
(true) or 0 (false).
The default value is true if you plot a ROC curve or an average ROC curve, and false otherwise.
In the ROC curve plot, the diagonal line represents a random classifier, and the line passing through [0,0], [0,1], and [1,1] represents a perfect classifier.
Example: ShowDiagonalLine=false
Data Types: single | double | logical
Flag to show the model operating point, specified as a
numeric or logical 1
(true) or 0
(false).
The default value is true for a ROC curve, and false
otherwise.
Example: ShowModelOperatingPoint=false
Data Types: single | double | logical
Metric for the x-axis, specified as a character vector or string scalar of the built-in metric name or a custom metric name, or a function handle (@metricName).
Built-in metrics — Specify one of the following built-in metric names by using a character vector or string scalar.
Name Description "TruePositives"or"tp"Number of true positives (TP) "FalseNegatives"or"fn"Number of false negatives (FN) "FalsePositives"or"fp"Number of false positives (FP) "TrueNegatives"or"tn"Number of true negatives (TN) "SumOfTrueAndFalsePositives"or"tp+fp"Sum of TP and FP "RateOfPositivePredictions"or"rpp"Rate of positive predictions (RPP), (TP+FP)/(TP+FN+FP+TN)"RateOfNegativePredictions"or"rnp"Rate of negative predictions (RNP), (TN+FN)/(TP+FN+FP+TN)"Accuracy"or"accu"Accuracy, (TP+TN)/(TP+FN+FP+TN)"TruePositiveRate","tpr", or"recall"True positive rate (TPR), also known as recall or sensitivity, TP/(TP+FN)"FalseNegativeRate","fnr", or"miss"False negative rate (FNR), or miss rate, FN/(TP+FN)"FalsePositiveRate"or"fpr"False positive rate (FPR), also known as fallout or 1-specificity, FP/(TN+FP)"TrueNegativeRate","tnr", or"spec"True negative rate (TNR), or specificity, TN/(TN+FP)"PositivePredictiveValue","ppv","prec", or"precision"Positive predictive value (PPV), or precision, TP/(TP+FP)"NegativePredictiveValue"or"npv"Negative predictive value (NPV), TN/(TN+FN)"f1score"F1 score, 2*TP/(2*TP+FP+FN)"ExpectedCost"or"ecost"Expected cost,
(TP*cost(P|P)+FN*cost(N|P)+FP*cost(P|N)+TN*cost(N|N))/(TP+FN+FP+TN), wherecostis a 2-by-2 misclassification cost matrix containing[0,cost(N|P);cost(P|N),0].cost(N|P)is the cost of misclassifying a positive class (P) as a negative class (N), andcost(P|N)is the cost of misclassifying a negative class as a positive class.The software converts the
K-by-Kmatrix specified by theCostname-value argument ofrocmetricsto a 2-by-2 matrix for each one-versus-all binary problem. For details, see Misclassification Cost Matrix.The software computes the scale vector using the prior class probabilities (
Prior) and the number of classes inLabels, and then scales the performance metrics according to this scale vector. For details, see Performance Metrics.Custom metric stored in the
Metricsproperty — Specify the name of a custom metric stored in theMetricsproperty of the input objectrocObj. Therocmetricsfunction names a custom metric"CustomMetricN", whereNis the number that refers to the custom metric. For example, specifyXAxisMetric="CustomMetric1"to use the first custom metric inMetricsas a metric for the x-axis.Custom metric — Specify a new custom metric by using a function handle. A custom function that returns a performance metric must have this form:
metric = customMetric(C,scale,cost)
The output argument
metricis a scalar value.A custom metric is a function of the confusion matrix (
C), scale vector (scale), and cost matrix (cost). The software finds these input values for each one-versus-all binary problem. For details, see Performance Metrics.Cis a2-by-2confusion matrix consisting of[TP,FN;FP,TN].scaleis a2-by-1scale vector.costis a2-by-2misclassification cost matrix.
The
plotfunction names a custom metric"Custom Metric"for the axis label.The software does not support cross-validation for a custom metric. Instead, you can specify to use bootstrap when you create a
rocmetricsobject.
If you specify a new metric instead of one in the Metrics property of
the input object rocObj, the plot function
computes and plots the metric values. If you compute confidence intervals when you
create rocObj, the plot function also computes
confidence intervals for the new metric.
The plot function ignores NaNs in the performance metric values. Note that the positive predictive value (PPV) is
NaN for the reject-all threshold for which TP = FP = 0, and the negative predictive value (NPV) is NaN for the
accept-all threshold for which TN = FN = 0. For more details, see Thresholds, Fixed Metric, and Fixed Metric Values.
Example: XAxisMetric="FalseNegativeRate"
Data Types: char | string | function_handle
Metric for the y-axis, specified as a character vector or string scalar of
the built-in metric name or custom metric name, or a function handle
(@metricName). For details, see XAxisMetric.
Example: YAxisMetric="FalseNegativeRate"
Data Types: char | string | function_handle
Output Arguments
Object for the performance curve, returned as a ROCCurve object or an array of ROCCurve objects. plot returns a ROCCurve object for each performance curve.
Use curveObj to query and modify properties of the plot after creating
it. For a list of properties, see ROCCurve Properties.
Graphics objects for the model operating points and diagonal line, returned as a graphics array containing Scatter and Line objects.
graphicsObjs contains a Scatter object for each model operating point (if ShowModelOperatingPoint=trueLine object for the diagonal line (if ShowDiagonalLine=truegraphicsObjs to query and modify properties of the model operating points and diagonal line after creating the plot. For a list of properties, see Scatter Properties and Line Properties.
More About
A ROC curve shows the true positive rate versus the false positive rate for different thresholds of classification scores.
The true positive rate and the false positive rate are defined as follows:
True positive rate (TPR), also known as recall or sensitivity —
TP/(TP+FN), where TP is the number of true positives and FN is the number of false negativesFalse positive rate (FPR), also known as fallout or 1-specificity —
FP/(TN+FP), where FP is the number of false positives and TN is the number of true negatives
Each point on a ROC curve corresponds to a pair of TPR and FPR values for a specific
threshold value. You can find different pairs of TPR and FPR values by varying the
threshold value, and then create a ROC curve using the pairs. For each class,
rocmetrics uses all distinct adjusted score values
as threshold values to create a ROC curve.
For a multiclass classification problem, rocmetrics formulates a set
of one-versus-all binary
classification problems to have one binary problem for each class, and finds a ROC
curve for each class using the corresponding binary problem. Each binary problem
assumes one class as positive and the rest as negative.
For a binary classification problem, if you specify the classification scores as a
matrix, rocmetrics formulates two one-versus-all binary
classification problems. Each of these problems treats one class as a positive class
and the other class as a negative class, and rocmetrics finds two
ROC curves. Use one of the curves to evaluate the binary classification
problem.
For more details, see ROC Curve and Performance Metrics.
The area under a ROC curve (AUC) corresponds to the integral of a ROC curve
(TPR values) with respect to FPR from FPR = 0 to FPR = 1.
The AUC provides an aggregate performance measure across all possible thresholds. The AUC
values are in the range 0 to 1, and larger AUC values
indicate better classifier performance.
The one-versus-all (OVA) coding design reduces a multiclass classification
problem to a set of binary classification problems. In this coding design, each binary
classification treats one class as positive and the rest of the classes as negative.
rocmetrics uses the OVA coding design for multiclass classification and
evaluates the performance on each class by using the binary classification that the class is
positive.
For example, the OVA coding design for three classes formulates three binary classifications:
Each row corresponds to a class, and each column corresponds to a binary
classification problem. The first binary classification assumes that class 1 is a positive
class and the rest of the classes are negative. rocmetrics evaluates the
performance on the first class by using the first binary classification problem.
Algorithms
For each class, rocmetrics adjusts the classification scores (input argument
Scores of rocmetrics) relative to the scores for the rest
of the classes if you specify Scores as a matrix. Specifically, the
adjusted score for a class given an observation is the difference between the score for the
class and the maximum value of the scores for the rest of the classes.
For example, if you have [s1,s2,s3] in a row of Scores for a classification problem with
three classes, the adjusted score values are [s1-max(s2,s3),s2-max(s1,s3),s3-max(s1,s2)].
rocmetrics computes the performance metrics using the adjusted score values
for each class.
For a binary classification problem, you can specify Scores as a
two-column matrix or a column vector. Using a two-column matrix is a simpler option because
the predict function of a classification object returns classification
scores as a matrix, which you can pass to rocmetrics. If you pass scores in
a two-column matrix, rocmetrics adjusts scores in the same way that it
adjusts scores for multiclass classification, and it computes performance metrics for both
classes. You can use the metric values for one of the two classes to evaluate the binary
classification problem. The metric values for a class returned by
rocmetrics when you pass a two-column matrix are equivalent to the
metric values returned by rocmetrics when you specify classification scores
for the class as a column vector.
References
[1] Sebastiani, Fabrizio. "Machine Learning in Automated Text Categorization." ACM Computing Surveys 34, no. 1 (March 2002): 1–47.
Version History
Introduced in R2022bplot(rocobj,ShowModelOperatingPoint=true)
plots the operating point for all curves in the plot, including averaged curves and non-ROC
curves. Previously, plot indicated the operating point only for ROC curves,
and not for averaged curves.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)