augoffset
Syntax
Description
For a state-space model with offsets, augoffset returns an
offset-free state-space model with one extra input channel.
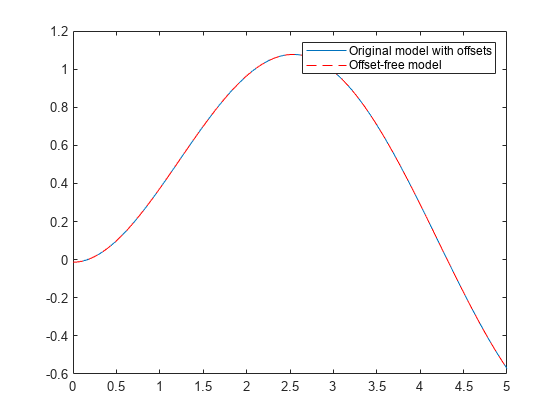
The function constructs a model such that the response of the original model to an input u(t) matches the response of the augmented model to [u(t) ; 1]. That is, the response of the augmented model is the same as the original model when you apply a unit step to the extra input channel and an input u(t) to the remaining input channels.
For a state-space model with offsets given by:
the transfer function of the augmented model is [H(s) h(s)], where H(s) and h(s) are the linear and affine parts of the original model, respectively. Therefore, the frequency response is the frequency-domain expression of the time-domain connection.
Here,
Note that H(s) is the usual transfer function without offsets.
You can use augoffset to turn offsets into an additional input and
visualize the corresponding frequency response.
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2024a