LPV System
Simulate linear parameter-varying (LPV) systems
Libraries:
Control System Toolbox /
Linear Parameter Varying
Description
A linear parameter-varying (LPV) system is a linear state-space model whose dynamics vary as a function of certain time-varying parameters called scheduling parameters. In MATLAB®, an LPV model is represented in a state-space form using coefficients that are parameter dependent.
Mathematically, you can represent an LPV system as follows.
Here:
u(t) are the inputs
y(t) are the outputs
x(t) are the model states with initial value xinit
is the state derivative vector for continuous-time systems and the state update vector x[k+1] for discrete-time systems. Here, k is the integer index that counts the number of sampling periods Ts.
A(p), B(p), C(p), and D(p) are the state-space matrices parameterized by the scheduling parameter vector p.
The parameters p = p(t) are measurable functions of the inputs and the states of the model. They can be a scalar quantity or a vector of several parameters. The set of scheduling parameters define the scheduling space over which the LPV model is defined.
dx0(p), x0(p), u0(p), and y0(p) are the offsets in the values of , x(t), u(t) and y(t) at a given parameter value p = p(t) or p[k].
You can obtain the offsets by returning additional linearization information when calling functions such as
linearize(Simulink Control Design) orgetIOTransfer(Simulink Control Design). For an example, see LPV Approximation of Boost Converter Model (Simulink Control Design).
Caution
Avoid making C(p) and D(p) depend on the system output y. Otherwise, the resulting state-space equation y = C(y)x + D(y)u creates an algebraic loop, because computing the output value y requires knowing the output value. This algebraic loop is prone to instability and divergence. Instead, try expressing C and D in terms of the time t, the block input u, and the state outputs x.
For similar reasons, avoid scheduling A(p) and B(p) based on the dx output. Note that it is safe for A and B to depend on y when y is a fixed combination of states and inputs (in other words, when y = Cx + Du, where C and D are constant matrices).
The block implements a grid-based representation of the LPV system. You pick a grid of
values for the scheduling parameters. At each value p =
p*, you specify the corresponding linear system as a state-space
(ss or idss (System Identification Toolbox)) model object. You use the generated array of state-space models to
configure the LPV System block.
The block accepts an array of state-space models with operating point information. The
block extracts the information on the scheduling variables from the
SamplingGrid property of the LTI array. The scheduling variables define
the grid of the LPV models. They are scalar-valued quantities that can be functions of time,
inputs and states, or constants. They are used to pick the local dynamics in the operating
space. The software interpolates the values of these variables. The block uses this array with
data interpolation and extrapolation techniques for simulation.
Examples
Consider a 2-input, 3-output, 4-state LPV model. Use input
u(2) and state x(1) as scheduling parameters.
Configure the Simulink® model as shown in the following figure.

Consider a linear mass-spring-damper system whose mass changes as a function of an external load command. The governing equation is as follows:
Here, is the mass dependent upon the external command , is the damping ratio, is the stiffness of the spring, and is the forcing input. is position of the mass at a given time . For a fixed value of , the system is linear and expressed as
,
where is the state vector and is the value of the mass for a given value of .
In this example, you want to study the model behavior over a range of input values from 1 to 10 Volts. For each value of , measure the mass and compute the linear representation of the system. Suppose mass is related to the input by the relationship . For values of u ranging from 1 to 10 results in the following array of linear systems.
c = 5; k = 300; u = 1:10; m = 10*u + 0.1*u.^2; for i = 1:length(u) A = [0 1; -k/m(i), -c/m(i)]; B = [0; 1/m(i)]; C = [1 0]; sys(:,:,i) = ss(A,B,C,0); end
The variable is the scheduling input. Add this information to the model.
sys.SamplingGrid = struct('LoadCommand',u);Configure the LPV System block:
Type
sysin the State-space array field.Connect the input port
parto a one-dimensional source signal that generates the values of the load command. If the source provides values between 1 and 10, the block uses interpolation to compute the linear model at a given time instance. Otherwise, the block uses extrapolation.

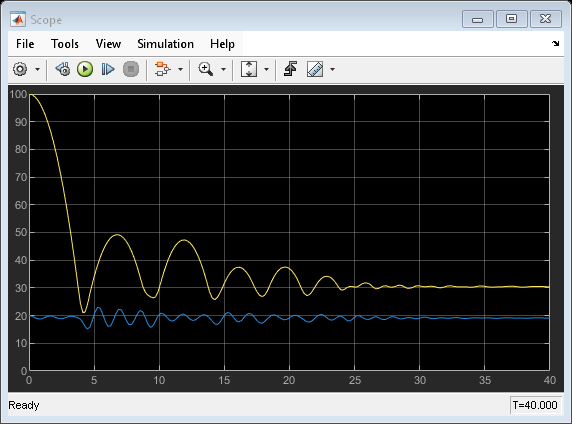
Simulate the LPV model to a constant forcing input of 100 N and random values for the load command scheduling variable.
model = "simMSDLPV";
open_system(model);
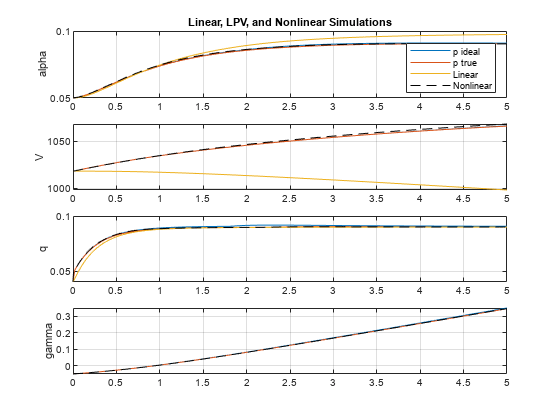
This example shows how to simulate a linear parameter-varying (LPV) model of an engine speed using the LPV System block. The LPV System block interpolates a state-space array to model the LPV response. Typically, you can obtain such an array by batch linearizing a nonlinear model over a range of operating conditions. This example provides a linearized result of the engine speed model in scdspeedlpvData. For more information about linearizing this model, see Linearize Engine Speed Model (Simulink Control Design).
Open the model.
model = "scdspeedLPVCompare";
open_system(model);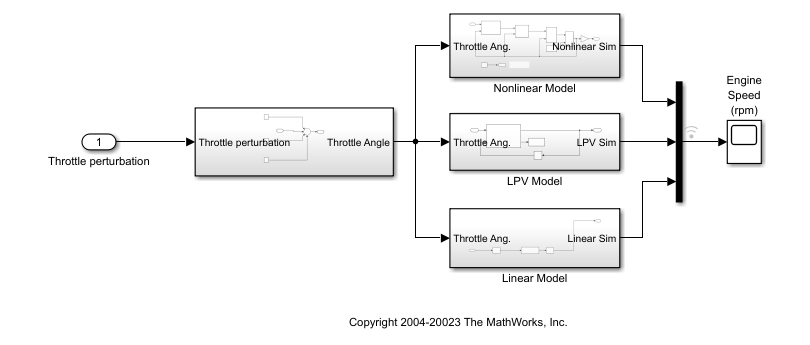
Load the linearization result for implementing the LPV model.
load scdspeedlpvData.matThe LPV model is implemented under the LPV Model subsystem.
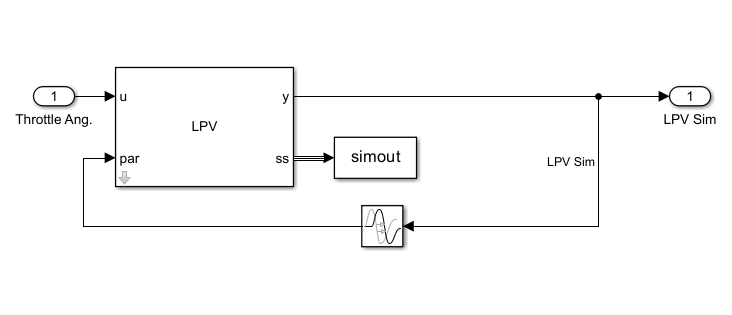
The LPV System block takes the throttle angle as an input and uses the speed output as scheduling variable. The block parameters are configured as shown in this image. Here, the state-space array sys and offsets are obtained by batch linearizing the nonlinear model.

Simulate the model and plot the response comparison.
sim(model);
plot(logsOut{1}.Values.Time,logsOut{1}.Values.Data)
grid on
legend("Nonlinear sim","LPV sim","LTI sim",Location="best")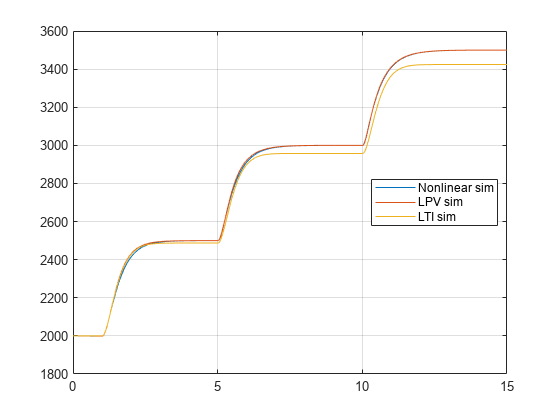
The LPV model provides a good approximation of the nonlinear response.
Extended Examples
LPV Approximation of Boost Converter Model
Approximate a nonlinear Simscape™ Electrical™ model using a linear parameter varying model.
(Simulink Control Design)
Design and Validate Gain-Scheduled Controller for Nonlinear Aircraft Pitch Dynamics
Approximate nonlinear behavior of airframe pitch axis dynamics using linear parameter-varying model.
Using LTI Arrays for Simulating Multi-Mode Dynamics
Construct a Linear Parameter Varying (LPV) representation of a system that exhibits multi-mode dynamics.
Approximate Nonlinear Behavior Using Array of LTI Systems
You can use linear parameter varying models to approximate the dynamics of nonlinear systems.
(Simulink Control Design)
Limitations
Internal delays cannot be extrapolated to be less than their minimum value in the state-space model array.
When using an scattered grid of linear models to define the LPV system, only the nearest neighbor interpolation scheme is used. This may reduce the accuracy of simulation results. It is recommended to work with rectangular grids created using
ndgrid.
Ports
Input
Specify the input signal u(t). In multi-input case, this port accepts a signal of the dimension of the input.
Provide the signals for variables defining the scheduling space (sampling grid variables). The scheduling variables can be functions of time, inputs and states, or constants. You can achieve the required dependence by preparing a scheduling signal using clock input (for time), input signal (u), the output state signals (x) of the LPV block, or any exogenous signals, as required.
Caution
Avoid making C(p) and D(p) depend on the system output y. Otherwise, the resulting state-space equation y = C(y)x + D(y)u creates an algebraic loop, because computing the output value y requires knowing the output value. This algebraic loop is prone to instability and divergence. Instead, try expressing C and D in terms of the time t, the block input u, and the state outputs x.
For similar reasons, avoid scheduling A(p) and B(p) based on the dx output. Note that it is safe to for A and B to depend on y when y is a fixed combination of states and inputs, (in other words, when y = Cx + Du where C and D are constant matrices).
Since R2024b
Initial conditions to use with the local model to start the simulation, specified as a vector of length equal to the number of model states.
Dependencies
To enable this port, set Initial condition source to
external.
Output
Response of the linear parameter-varying model.
Values of the model states.
Dependencies
To enable this port, select Output states on the Outputs tab of the block parameters.
Values of the state derivatives. The state derivatives are sometimes used to define the scheduling parameters. However, avoid scheduling A and B based on the dx output.
Dependencies
To enable this port, select Output state derivatives (continuous-time) or updates (discrete-time) on the Outputs tab of the block parameters.
Local state-space model data at the major simulation time steps, returned as a bus signal with these elements.
A— State matrixB— Input matrixC— Output matrixD— Feedthrough matrixInputDelay— Input delayOutputDelay— Output delayInternalDelay— Internal delays in the model
Dependencies
To enable this port, select Output interpolated state-space data on the Outputs tab of the block parameters.
LPV model offset data at the major simulation time steps, returned as a bus signal with these elements.
InputOffsetOutputOffsetStateOffsetStateDerivativeOffset
Dependencies
To enable this port, select Output interpolated offsets on the Outputs tab of the block parameters.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
LPV Model Tab
An array of state-space (ss or idss (System Identification Toolbox)) models. All the models in the
array must use the same definition of states.
The state-space array must specify scheduling parameters and the interpolation
grid for the model in the SamplingGrid property. You can also
specify the model offsets in the Offsets property of the array when
you set the Operating Point Offsets parameter to Use
offsets in state-space array, See the ss model
reference page for more information on these properties.
When the block is in a model with synchronous state control (see the State Control (HDL Coder) block), you must specify an array of discrete-time models.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | sys |
| Values: | ss or idss model array name in
quotes |
Example: set_param(gcb,"sys","sysArrayName")
Since R2024b
Specify the initial condition source.
internal— Specify the initial conditions of the states using the Initial condition parameter.external— Specify the initial conditions of the states at the IC input port of the block.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | InitialConditionSource |
| Values: | internal (default) | external |
Initial conditions to use with the local model to start the simulation, specified as a vector of length equal to the number of model states.
Dependencies
To enable this parameter, set Initial condition source to
internal.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | InitialCondition |
| Values: | "0" (default) | initial state values in quotes |
Example: set_param(gcb,"InitialCondition","[0
0.1]")
Since R2024a
Specify the format for operating point offsets.
Specify Offsets as double arrays— Specify offsets using the Input offset, Output offset, State Offset, and State derivative/update offset parameters.Specify offsets as struct array— Specify offsets as a structure array with fieldsu,y,x, anddxspecifying the input, output, state, and state derivative offsets, respectively.Use offsets in state-space array— Use the offsets specified in theOffsetsproperty of the state-space array.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | opSpecOption |
| Values: | "Specify Offsets as double
arrays" (default) | "Specify offsets as struct array" | "Use offsets in state-space array" |
Example: set_param(gcb,"opSpecOption","Specify offsets as struct
array")
Offsets in input u(t), specified as one of the
following:
0— Use when there are no input offsets ().Double vector of length equal to the number of inputs — Use when input offset is the same across the scheduling space.
Double array of size nu-by-1-by-N1-by-
...-by-Nm — Use when offsets are present and they vary across the scheduling space. Here, nu is the number of inputs and N1-by-...-by-Nm is the size of the scheduling grid. For example, if your model has three inputs, two outputs, and four states and is scheduled over a 5-by-6 grid of operating points, the input array size must be 3-by-1-by-5-by-6. Usesize(sys)to determine the size of the state-space arraysys.
Dependencies
To enable this parameter, set the Operating Point Offsets
format to Specify Offsets as double arrays.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | uOffset |
| Values: | "0" (default) | array name in quotes |
Example: set_param(gcb,"uOffset","uOffArray")
Offsets in output y(t), specified as one of the
following:
0— Use when there are no output offsets .Double vector of length equal to the number of outputs — Use when output offsets are the same across the scheduling space.
Double array of size ny-by-1-by-N1-by-
...-by-Nm — Use when offsets are present and they vary across the scheduling space. Here, ny is the number of outputs and N1-by-...-by-Nm is the size of the scheduling grid. For example, if your model has three inputs, two outputs, and four states and is scheduled over a 5-by-6 grid of operating points, the input array size must be 2-by-1-by-5-by-6. Usesize(sys)to determine the size of the state-space arraysys.
Dependencies
To enable this parameter, set the Operating Point Offsets
format to Specify Offsets as double arrays.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | yOffset |
| Values: | "0" (default) | array name in quotes |
Example: set_param(gcb,"yOffset","yOffArray")
Offsets in states x(t), specified as one of the
following:
0— Use when there are no state offsets .Double vector of length equal to the number of states — Use when the state offsets are the same across the scheduling space.
Double array of size nx-by-1-by-N1-by-
...-by-Nm — Use when offsets are present and they vary across the scheduling space. Here, nx is the number of states and N1-by-...-by-Nm is the size of the scheduling grid. For example, if your model has three inputs, two outputs, and four states and is scheduled over a 5-by-6 grid of operating points, the input array size must be 4-by-1-by-5-by-6. Usesize(sys)to determine the size of the state-space arraysys.
Dependencies
To enable this parameter, set the Operating Point Offsets
format to Specify Offsets as double arrays.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | xOffset |
| Values: | "0" (default) | array name in quotes |
Example: set_param(gcb,"xOffset","xOffArray")
Offsets in state derivative or update variable dx(t), specified
as one of the following:
If you obtained the linear system array by linearization under equilibrium conditions, select the Assume equilibrium operating conditions option. This option corresponds to an offset of for a continuous-time system and for a discrete-time system. This option is selected by default.
If the linear system contains at least one system that you obtained under non-equilibrium conditions, clear the Assume equilibrium operating conditions option. Specify one of the following in the Offset value field:
Double vector of length equal to the number of states — Use when the state derivative offsets are the same across the scheduling space.
Double array of size nx-by-1-by-N1-by-
...-by-Nm — Use when offsets are present and they vary across the scheduling space. Here, nx is the number of states and N1-by-...-by-Nm is the size of the scheduling grid. For example, if your model has three inputs, two outputs, and four states and is scheduled over a 5-by-6 grid of operating points, the input array size must be 4-by-1-by-5-by-6. Usesize(sys)to determine the size of the state-space arraysys.
Dependencies
To enable this parameter, set the Operating Point Offsets
format to Specify Offsets as double arrays and disable
Assume equilibrium operating conditions.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | dxOffset |
| Values: | "0" (default) | array name in quotes |
Example: set_param(gcb,"dxOffset","dxOffArray")
Since R2024a
Model offsets, specified as a structure with these fields.
| Field | Description |
|---|---|
u | Input offsets |
y | Output offsets |
x | State offsets |
dx | State derivative offsets |
If offset values are the same across the scheduling space, specify as a double vector of length equal to the number of inputs, outputs, or states for the corresponding fields.
If the offsets vary across scheduling space, specify a structure array. For instance, suppose that your model has three inputs, two outputs, and four states. If you linearize your model using a 5-by-6 array of operating points, the structure array size must be 5-by-6 and each entry must contain a vector of length equal to the number of inputs, outputs, or states for the corresponding fields.
The linearize (Simulink Control Design) function returns offsets in
this format in the info.Offsets output when you linearize with
StoreOffsets option set to true.
Dependencies
To enable this parameter, set the
Operating Point Offsets format to Specify
Offsets as struct array. (since R2024a)
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | Offset |
| Values: | "struct" (default) | structure array name in quotes |
Example: set_param(gcb,"Offset","OffsetStructName")
Fixed Entries Tab
In certain cases, your LPV model may contain coefficients with small variations. Using the parameters on this tab, you can specify which model matrices are fixed and their nominal values to override entries in model data. In some situations, you may want to replace a parameter-dependent matrix such as A(p) with a fixed value A* for simulation. For example, A* may represent an average value over the scheduling range. By default, the block uses the State-space array data to decide which entries are fixed and which entries vary (for performance reasons, the block only interpolates varying entries).
With this tab, you can override this default behavior, for example, to try and simplify
the LPV model. For example, you can decide that the third entry of A does
not vary much and that you want to fix it to its average value. The logical arrays specify
which entries should be treated as fixed, and Read values from
specifies which value to use for these fixed entries. false corresponds
to not overriding the LTI array data, that is, rely on the data to decide whether this entry
is fixed or varying.
Specify the location of these coefficients as one of the following:
Scalar Boolean (
trueorfalse), if all entries of a matrix are to be treated the same way.The default value is
falsefor the state-space matrices and delay vectors, which means that they are treated as free.Logical matrix of a size compatible with the size of the corresponding matrix:
State-space matrix
Size of fixed entry matrix
A matrix nx-by-nx
B matrix nx-by-nu
C matrix ny-by-nx
D matrix ny-by-nu
Input delay nu-by-1
Output delay ny-by-1
Internal delay ni-by-1
where, nu is the number of inputs, ny is the number of outputs, nx is the number of states, ni is the length of internal delay vector.
Numerical indices to specify the location of fixed entries. See
sub2indreference page for more information on how to generate numerical indices corresponding to a given subscript(i,j)for an element of a matrix.
After you specify the location, provide the values of fixed coefficient using the Read values from parameter.
State-space model that provides the values of the fixed coefficients, specified as one of the following:
First model in state-space array— The first model in the state-space array is used for the fixed coefficients of the LPV model. In the following example, the state-space array is specified by objectsysand the fixed coefficients are taken from modelsys(:,:,1).% Specify a 4-by-5 array of state-space models. sys = rss(4,2,3,4,5); a = 1:4; b = 10:10:50; [av,bv] = ndgrid(a,b); % Use "alpha" and "beta" variables as scheduling parameters. sys.SamplingGrid = struct('alpha',av,'beta',bv);
Fixed coefficients are taken from the model
sysFixed = sys(:,:,1), which corresponds to[alpha=1, beta=10]. If the (2,1) entry ofAmatrix is forced to be fixed, its value used during the simulation issysFixed.A(2,1).Custom state-space model— Specify a different state-space model for fixed entries. Specify a variable for the fixed model in the Custom model field. The fixed model must use the same state basis as the state-space array in the LPV model.
Scheduling Tab
Interpolation method. Defines how the state-space data must be computed for scheduling parameter values that are located away from their grid locations.
Specify one of the following options:
Flat— Choose the state-space data at the grid point closest, but not larger than, the current point. The current point is the value of the scheduling parameters at current time.Nearest— Choose the state-space data at the closest grid point in the scheduling space.Linear— Obtain state-space data by linear interpolation of the nearest 2d neighbors in the scheduling space, where d = number of scheduling parameters.
The default interpolation scheme is Linear for regular
grids of scheduling parameter values. For irregular grids, the
Nearest interpolation scheme is always used regardless of
the choice you made. To learn more about regular and irregular grids, see Regular vs. Irregular Grids.
The Linear method provides the highest accuracy but
takes longer to compute. The Flat and
Nearest methods are good for models that have
mode-switching dynamics.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | IMethod |
| Values: | "Linear" (default) | "Nearest" | "Flat" |
Example: set_param(gcb,"IMethod","Flat")
Extrapolation method. Defines how to compute the state-space data for scheduling
parameter values that fall outside the range over which the state-space array has been
provided (as specified in the SamplingGrid property).
Specify one of the following options:
Clip(default) — Disables extrapolation and returns the data corresponding to the last available scheduling grid point that is closest to the current point.Linear— Fits a line between the first or last pair of values for each scheduling parameter, depending upon whether the current value is less than the first or greater than the last grid point value, respectively. This method returns the point on that line corresponding to the current value. Linear extrapolation requires that the interpolation scheme be linear too.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | EMethod |
| Values: | "Clip" (default) | "Linear" |
Example: set_param(gcb,"EMethod","Linear")
The block determines the location of the current scheduling parameter values in
the scheduling space using a prelookup algorithm. Select Linear
search or Binary search. Each search method
has speed advantages in different situations. For more information on this parameter,
see the Prelookup (Simulink) block reference page.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
To get the block parameter value
programmatically, use the get_param (Simulink) function.
| Parameter: | IndexSearch |
| Values: | "Binary Search" (default) | "Linear Search" |
Example: set_param(gcb,"IndexSearch","Linear
Search")
Select this check box when you want the block to start its search using the index found at the previous time step. For more information on this parameter, see the Prelookup (Simulink) block reference page.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | IndexBegin |
| Values: | "on" (default) | "off" |
Example: set_param(gcb,"IndexBegin","off")
Code Generation Tab
Block data type, specified as double or
single.
Dependencies
To enable this option, use a discrete-time state-space model as input.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | DataType |
| Values: | "double" (default) | "single" |
Example: set_param(gcb,"DataType","single")
Initial memory allocation for the number of input points to store for models that contain delays. If the number of input points exceeds the initial buffer size, the block allocates additional memory. The default size is 1024.
When you run the model in Accelerator mode or build the model, make sure the initial buffer size is large enough to handle maximum anticipated delay in the model.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | InitBufferSize |
| Values: | "1024" (default) | positive integer greater than 5 in quotes |
Example: set_param(gcb,"InitBufferSize","512")
Specify whether to use a fixed buffer size to save delayed input and output data from previous time steps. Use this option for continuous-time LPV systems that contain input or output delays. If the buffer is full, new data replaces data already in the buffer. The software uses linear extrapolation to estimate output values that are not in the buffer.
Programmatic Use
To set the block parameter value programmatically, use
the set_param (Simulink) function.
| Parameter: | FixedBuffer |
| Values: | "off" (default) | "on" |
Example: set_param(gcb,"FixedBuffer","on")
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2014bThe LPV System block now allows you to specify initial state values at
the block input port IC. To enable this port, set the Initial
condition source parameter to external.
The Initial state parameter x0 is now called
InitialCondition. If your code sets this parameter programmatically
using, for example set_param(blockPath,"x0","[0 0.1]"), update your code
to set_param(blockPath,"InitialCondition","[0 0.1]").
The LPV System block now supports specifying operating point offsets in two new formats:
Specify offsets as struct array
Use offsets in state-space array
Before R2024a, the block supported specifying offsets only as double arrays in the block parameters. Use the Operating Point Offsets list to specify the format of offsets.
Additionally, the block has the following new enhancements:
The block architecture now uses a Varying State Space block underneath. This streamlines the support for offsets.
The block now supports fast restart for simulation. In this mode, only the block inputs and the Initial state parameter are tunable. The rest of the block parameters are non tunable because changing them alters the model topology.
The LPV System block now ignores singleton dimension and constant
parameters in the sampling grid of the input model array. Therefore, you must not feed the
parameters, that is, the fields of the SamplingGrid structure with
constant values to the par port of the block. Use only the varying
fields with this port.
Before R2024a, the block returned an error when fed parameters with constant values.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)