Offline Training and Testing of PyTorch Model for CSI Feedback Compression

Since R2025a

This example shows how to perform offline training and testing of a PyTorch® autoencoder based neural network for channel state information (CSI) feedback compression.

In this example, you:

1. Train an autoencoder-based neural network.

2. Test the trained neural network.

3. Compare the performance metrics of the complex input lightweight neural network (CLNet) PyTorch model across multiple compression factors.

Introduction

In 5G networks, efficient handling of CSI is crucial for optimizing downlink data transmission. Traditional methods rely on feedback mechanisms where the user equipment (UE) processes the channel estimate to reduce the CSI feedback data sent to the access node (gNB). However, an innovative approach involves using an autoencoder-based neural networks to compress and decompress the CSI feedback more effectively.

In this example, you define, train, test, and compare the performance of the following autoencoder model:

• Complex input lightweight neural network (CLNet): CLNet is a lightweight neural network designed for massive multiple-input multiple-output (MIMO) CSI feedback, which utilizes complex-valued inputs and attention mechanisms to improve accuracy while reducing computational overhead [1].

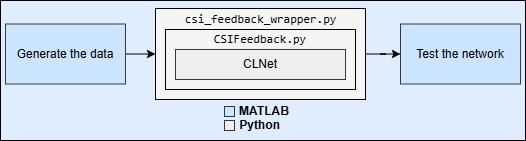
Set Up Python Environment

Set up the Python® environment as described in PyTorch Coexecution before running the example. Specify the full path of the Python executable to use below. The helperSetupPyenv function sets the Python Environment in MATLAB® based on the selected options and checks that the libraries listed in the requirements_csi_feedback.txt file are installed.

If you use Windows®, provide the path to the pythonw.exe file.

if ispc
    exePath = "..\python\pythonw.exe";
else
    exePath = "../python/python/bin/python3";
end
exeMode = "OutOfProcess";
currentPenv = helperSetupPyenv(exePath,exeMode,"requirements_csi_feedback.txt");

Setting up Python environment
Parsing requirements_csi_feedback.txt 
Checking required package 'numpy'
Checking required package 'torch'
Required Python libraries are installed.

Prepare Data

Prepare training, validation, and testing data. You train the autoencoder-based neural network using the training and validation data, then evaluate its performance using the test data.

Carrier Configuration

Set the number of resource blocks to 52 and subcarrier spacing to 15.

sysOpt.NSizeGrid = 52;                           % Number resource blocks (RB)
sysOpt.SubcarrierSpacing = 15; % 15, 30, 60, 120 kHz

Create an nrCarrierConfig object and set the carrier parameters.

carrier = nrCarrierConfig;
carrier.NSizeGrid = sysOpt.NSizeGrid;
carrier.SubcarrierSpacing = sysOpt.SubcarrierSpacing;
waveInfo = nrOFDMInfo(carrier);

Configure MIMO Channel

Specify the transmit antenna size and receive antenna size.

sysOpt.TxAntennaSize = [2 2 2 1 1];   % rows, columns, polarization, panels
sysOpt.RxAntennaSize = [2 1 1 1 1];   % rows, columns, polarization, panels
sysOpt.MaxDoppler = 5;                % Hz
sysOpt.RMSDelaySpread = 300e-9;       % s
numSubCarriers = sysOpt.NSizeGrid*12; % 12 subcarriers per RB

Select a delay profile to represent the MIMO fading channel.

sysOpt.DelayProfile = "CDL-C"; % CDL-A, CDL-B, CDL-C, CDL-D, CDL-D, CDL-E

Create an nrCDLChannel object and set the channel parameters.

samplesPerSlot = ...
  sum(waveInfo.SymbolLengths(1:waveInfo.SymbolsPerSlot));

channel = nrCDLChannel;
channel.DelayProfile = sysOpt.DelayProfile;
channel.DelaySpread = sysOpt.RMSDelaySpread;     % s
channel.MaximumDopplerShift = sysOpt.MaxDoppler; % Hz
channel.RandomStream = "Global stream";
channel.TransmitAntennaArray.Size = sysOpt.TxAntennaSize;
channel.ReceiveAntennaArray.Size = sysOpt.RxAntennaSize;
channel.ChannelFiltering = false;        % No filtering for 
                                         % perfect estimate
channel.NumTimeSamples = samplesPerSlot; % 1 slot worth of samples
channel.SampleRate = waveInfo.SampleRate;

Select Data Source

Specify the source of the data set for the CSI feedback autoencoder to be one of the following:

• downloadDataset: Downloads the data set with the configurations specified in Prepare Data for CSI Processing example.

• generateDataset: Generates the data set based on the selected configurations.

• loadDataset: Loads the data set from an existing directory.

For more information about how to generate and prepare data set for different CSI feedback autoencoders, see Prepare Data for CSI Processing example.

datasetSource = "generateDataset";

if datasetSource == "generateDataset"
    sysOpt.TruncationFactor     = 10;
    sysOpt.DataDomain           = "Frequency-Spatial";
    sysOpt.NumSlotsPerFrame     = 1;
    sysOpt.ResetChannelPerFrame = true;
    sysOpt.Preprocess           = true;
    sysOpt.UseParallel          = false;
    sysOpt.SaveData             = true;
    sysOpt.DataDir              = "Data";
    sysOpt.DataFilePrefix       = "CH_est";
    numSamples                  = 1500;
    sysOpt.ZeroTimingOffset     = false;
    sysOpt.Normalization        = false;
    sysOpt.Verbose              = true;
    numFrames = numSamples / prod(sysOpt.RxAntennaSize);
    if sysOpt.SaveData && exist(fullfile(".",sysOpt.DataDir),"dir")
        rmdir(sysOpt.DataDir,"s")
    end
    [~,HReal] = helperCSIGenerateData(numFrames,channel,carrier,sysOpt);
    [nDelay,nTx,nIQ,nRx,nFrames] = size(HReal);
    HReal = reshape(HReal,[nDelay,nTx,nIQ,nRx*nFrames]);
else
    dataDir = fullfile(pwd,"Data","processed"); % Path to the data set directory
    dataFilePrefix = "CH_est";                  % Filename prefix used in the data set
    if datasetSource == "downloadDataset"
        helperCSIDownloadFiles("pytorch dataset");
        dataDir = fullfile(pwd,"processed");
    end    

Load the prepared data set in to the workspace using the signalDatastore object. The signal datastore object uses individual files for each data point:

    sds = signalDatastore(fullfile(dataDir,dataFilePrefix+"_processed*"));
    HRealCell = readall(sds);
    HReal = cat(4,HRealCell{:});
end

Starting CSI data generation
1 worker(s) running
00:00:04 -  7% Completed
00:00:12 - 20% Completed
00:00:19 - 33% Completed
00:00:27 - 47% Completed
00:00:34 - 60% Completed
00:00:41 - 73% Completed
00:00:48 - 87% Completed
00:00:56 - 100% Completed

Split Data Set into Training, Validation, and Testing Data

Split the prepared data into training, validation and testing datasets. In this example, you use the helperCSISplitData function to split the prepared data in to a ratio of 10:3:2, where 10, 3, and 2 correspond to training, validation, and testing splits.

splitRatio = [10,3,2]; % Split ratio for training, validation and testing
[HTReal, HVReal, HTestReal] = helperCSISplitData(HReal,splitRatio);

Normalize Data Set

Normalize the data set to achieve zero mean and a target standard deviation of 0.0212, restricting most values to the range of [-0.5, 0.5].

[HTReal, HVReal, HTestReal, norm] = helperCSINormalizeData(HTReal, HVReal, HTestReal);

Define Neural Network

Next, define the CSI feedback autoencoder.

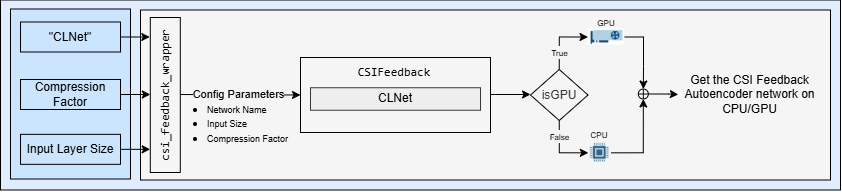
Specify the autoencoder-based neural network.

autoencoderNetwork = "CLNet";

Select a compression factor. Increasing the compression factor decreases the accuracy of the decompressed output because the network retains less information.

compressionFactor = 4;

Call the construct_model function in the Python wrapper file csi_feedback_wrapper.py to initialize and return the network using the specified parameters. It acts as an interface between MATLAB and Python.

inputLayerSize = size(HReal);  % Input layer size is calculated from the prepared data
pyCSINN = py.csi_feedback_wrapper.construct_model(autoencoderNetwork, inputLayerSize, compressionFactor);

Selected device: CPU

Train Neural Network

Set the training parameters to optimize the network performance. Set the maxEpochs to 1000 and numSamples to 150000 here to ensure complete training of the network.

initialLearningRate  = 0.0001; % Enter initial learning rate for training
maxEpochs            = 2;      % Number of epochs for training
miniBatchSize        = 1000;   % Mini-batch size for training

Use train method in Python wrapper file to set up the trainer with the training parameters in Python and train the PyTorch model.

results = py.csi_feedback_wrapper.train(...
  pyCSINN, ...
  HTReal, HVReal, HTestReal, ...
  initialLearningRate, ...
  maxEpochs, ...
  miniBatchSize);

Selected device: CPU
Epoch: 1
I 14:13:26] => Train  Loss: 2.783e-02


=! Best Validation rho: 5.178e-01 (Corresponding nmse=1.902e+01; epoch=1)
   Best Validation NMSE: 1.902e+01 (Corresponding rho=5.178e-01;  epoch=1)

Epoch: 2

I 14:13:26] => Train  Loss: 2.658e-02


=! Best Validation rho: 5.210e-01 (Corresponding nmse=1.881e+01; epoch=2)
   Best Validation NMSE: 1.881e+01 (Corresponding rho=5.210e-01;  epoch=2)

trainedNet = results{1};
training_loss = results{2};
validation_loss = results{3};

Test Neural Network

Use the predict method to process the test data.

tic;
HPredReal = single(py.csi_feedback_wrapper.predict(trainedNet,HTestReal));

Selected device: CPU

elapsedTime = toc;

Calculate the correlation and normalized mean squared error (NMSE) between the input and output of the autoencoder network.

The correlation is defined as

$$\rho =\mathbb{E}\left\{\frac{1}{N}\sum _{n=1}^N\frac{|{\underset{}{\overset{ˆ}{h}}}_n^H{h}_n|}{\Vert {\underset{}{\overset{ˆ}{h}}}_n{\Vert }_2\Vert h_n{\Vert }_2}\right\}$$

where, $$h_n$$ is the channel estimate at the input of the autoencoder and $${\underset{}{\overset{ˆ}{h}}}_n$$ is the channel estimate at the output of the autoencoder.

NMSE is defined as

$$NMSE=\mathbb{E}\left\{\frac{{\Vert H-\underset{}{\overset{ˆ}{H}}\Vert }_2^2}{{\Vert H\Vert }_2^2}\right\}$$

where, $$H$$ is the channel estimate at the input of the autoencoder and $$\underset{}{\overset{ˆ}{H}}$$ is the channel estimate at the output of the autoencoder.

HTestComplex = squeeze(complex(HTestReal(:,:,1,:), HTestReal(:,:,2,:)));
HPredComplex = squeeze(complex(HPredReal(:,:,1,:), HPredReal(:,:,2,:)));
rho = abs(helperComplexCosineSimilarity(HTestComplex, HPredComplex)); % Compute complex cosine similarity
meanRho = mean(rho);
[nmse,meanNmse] = helperCSINMSELossdB(HTestComplex, HPredComplex);    % Compute NMSE
helperPlotMetrics(rho, meanRho, nmse, meanNmse);

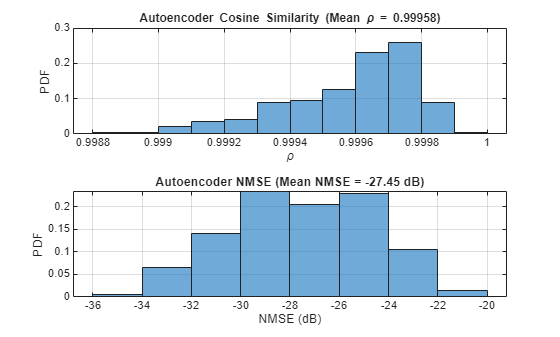
metricsTable = table(autoencoderNetwork, compressionFactor, meanNmse, meanRho, ...
  elapsedTime, single(py.csi_feedback_wrapper.info(pyCSINN)), ...
    'VariableNames', {'Model', 'Compression Factor', 'NMSE(dB)', ...
    'Rho', 'InferenceTime', 'NumberOfLearnables'});
disp(metricsTable)

     Model     Compression Factor    NMSE(dB)      Rho      InferenceTime    NumberOfLearnables
    _______    __________________    ________    _______    _____________    __________________

    "CLNet"            4             -27.446     0.99958       4.2413            1.0289e+05    

Save Trained Network

Enable saveNetwork to save the trained model in a PT file with the filename as checkPointName.

saveNetwork = true;
if saveNetwork % Save the trained network
    checkPointName = autoencoderNetwork+string(compressionFactor);
    py.csi_feedback_wrapper.save(trainedNet,checkPointName,autoencoderNetwork, inputLayerSize, compressionFactor);
end

Compare Networks

The following table compares the performance metrics, inference time, and learnable parameters of CLNet across compression factors 4, 16, and 64.

Model	Compression Factor	NMSE(dB)	Rho	Inference Time	Number of Learnables
CLNet	4	-46.639	0.99999	0.14911	1.0289e05
CLNet	16	-44.06	0.99998	0.18851	27538
CLNet	64	-35.524	0.99983	0.15048	8701

Further Exploration

In this example, you train and test the PyTorch network, CLNet using offline training. The CSI feedback autoencoder architecture achieves comparable NMSE and cosine similarity performance across different compression ratios. Adjust the data generation parameters and optimize hyperparameters for your specific use case.

For more information about online training and throughput analysis, see these examples:

• Online Training and Testing of PyTorch Model for CSI Feedback Compression

• NR PDSCH Throughput Using Channel State Information Feedback (5G Toolbox)

References

[1] Ji, S., & Li, M. (2021). CLNet: Complex Input Lightweight Neural Network Designed for Massive MIMO CSI Feedback. IEEE Wireless Communications Letters, 10(10), 2318–2322. doi:10.1109/lwc.2021.3100493.

Helper Functions

• helperSetupPyenv.m

• helperinstalledlibs.py

• helperLibraryChecker.m

• helperCSIDownloadFiles.m

• helperCSIGenerateData.m

• helperCSIChannelEstimate.m

• helperCSIPreprocessChannelEstimate.m

• helperCSISplitData.m

• CSIFeedback.py

• clnet.py

• csi_feedback_wrapper.py

• helperCSINMSELossdB.m

• helperNMSE.m

• helperComplexCosineSimilarity.m

PyTorch Wrapper Template

You can use your own PyTorch models in MATLAB using the Python interface. The py_wrapper_template.py file provides a simple interface with a predefined API. This example uses the following API set:

• construct_model: returns the PyTorch neural network model

• train: trains the PyTorch model

• setup_trainer: sets up a trainer object for with online training

• train_one_iteration: trains the PyTorch model for one iteration for online training

• validate: validates the PyTorch model for online training

• predict: runs the PyTorch model with the provided input(s)

• save: saves the PyTorch model and metadata

• load: loads the PyTorch model

• info: prints or returns information on the PyTorch model

The Train PyTorch Channel Prediction Models example shows a training workflow and uses the following API set in addition to the one used in this example.

• save_model_weights: saves the PyTorch model weights

• load_model_weights: loads the PyTorch model weights

You can modify the py_wrapper_template.py file. Follow the instruction in the template file to implement the recommended entry points. Delete the entry points that are not relevant to your project. Use the entry point functions as shown in this example to use your own PyTorch models in MATLAB.

Local Functions

function varargout = helperCSINormalizeData(varargin)
%helperCSINormalizeData Normalize the given inputs and return the
%normalization parameters
H = cat(4,varargin{:});
meanValue = mean(H,'all');
stdValue = std(H,[],'all');
targetStd = 0.0212;
for i=1:numel(varargin)
    varargout{i} = (varargin{i}-meanValue)/stdValue*targetStd+0.5;
end
norm.MeanVal = meanValue;
norm.StdValue = stdValue;
norm.TargetSTDValue = targetStd;
varargout{i+1} = norm;
end

function helperPlotMetrics(rho,meanRho,nmse,meanNmse)
%helperPlotMetrics Plot the histograms for RHO and NMSE values
figure
tiledlayout(2,1)
nexttile
histogram(rho,"Normalization","probability")
grid on
title(sprintf("Autoencoder Cosine Similarity (Mean \\rho = %1.5f)", ...
    meanRho))
xlabel("\rho"); ylabel("PDF")
nexttile
histogram(nmse,"Normalization","probability")
grid on
title(sprintf("Autoencoder NMSE (Mean NMSE = %1.2f dB)",meanNmse))
xlabel("NMSE (dB)"); ylabel("PDF")
end