timingEstimate

Estimate timing offset for communication signals

Since R2024a

Syntax

[offset,normcorr] = timingEstimate(waveform,refsig)

[offset,normcorr] = timingEstimate(___,name=value)

Description

[offset,normcorr] = timingEstimate(waveform,refsig) performs timing estimation by cross-correlating the input waveform and a known reference signal.

[offset,normcorr] = timingEstimate(___,name=value) specifies additional name-value arguments for detection threshold and window length.

Examples

Estimate Timing Offset of QPSK Signals

Generate a QPSK reference signal and input waveform. Fix the random seed.

 s = rng(123);
refSignal = pskmod(randi([0 3],[512 1]),4,pi/4);
waveform = pskmod(randi([0 3],[512 1]),4,pi/4);

Check the timing offset by using the reference signal as both inputs. Expected offset is 0.

offset1 = timingEstimate(refSignal,refSignal)

offset1 = 
0

Check the timing offset between the input waveform and the reference signal.

offset2 = timingEstimate(waveform,refSignal) % Expected offset is []

offset2 =

     []

offset3 = timingEstimate([zeros(5,1);refSignal],refSignal) % Expected offset is 5

offset3 = 
5

offset4 = timingEstimate([refSignal(2:end);0],refSignal) % Expected offset is -1

offset4 = 
-1

Generate a noise waveform input to compare with the reference signal.

noisyWaveform = awgn(refSignal,-15,'measured');

Estimate the timing offset and the normalized correlation magnitude between the noisy waveform and the reference signal.

[offset5, normCorr] = timingEstimate(noisyWaveform,refSignal) % Expected offset is []

offset5 =

     []

normCorr = 1023×1

    0.0442
    0.0198
    0.0066
    0.0462
    0.0556
    0.0391
    0.0425
    0.0149
    0.0185
    0.0532
    0.0680
    0.0080
    0.0284
    0.0642
    0.0193
      ⋮

Adjust the threshold to control the probability of missed detection. If needed, collect more normalized correlation data.

histogram(normCorr(:)) 

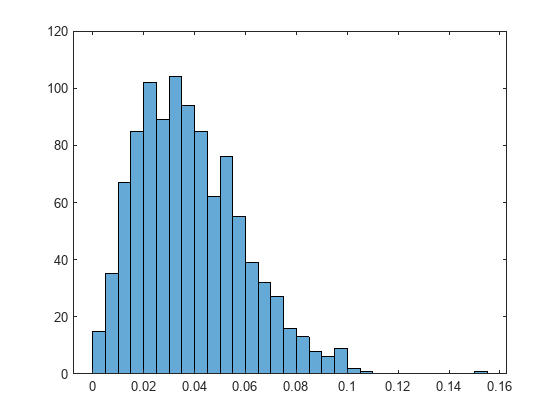
offset6 = timingEstimate(noisyWaveform,refSignal,Threshold=0.05) % Expected offset is 0

offset6 = 
0

Restore random seed.

rng(s);

Use WindowLength to Reduce Intersymbol Interference

Adjust the window length for a timing offset estimate to reduce intersymbol interference (ISI) in orthogonal frequency division multiplexing (OFDM) transmission.

Specify the OFDM parameters.

nfft = 512;
cplen = 16;
symLen = nfft + cplen;
nullIdx = [1:6 nfft/2+1 nfft-5:nfft]';
numDataCarrs = nfft-length(nullIdx);
modOrder = 64;
 

Generate the OFDM signal. Fix the random seed.

s = rng(123);
numSym = 100;
srcBits = randi([0,1], [numDataCarrs*log2(modOrder) numSym+2]);
ofdmData = qammod(srcBits,modOrder,InputType='bit', ...
            UnitAveragePower=true);
txSignal = ofdmmod(ofdmData,nfft,cplen,nullIdx); 

Use the second OFDM symbol as a reference signal.

refSig = txSignal(symLen+(1:symLen));

Generate a channel filter randomly. Make h(4) the biggest peak.

h = 10*randn(cplen+1,1,'like',1j);
h(4) = h(4)/abs(h(4))*(2*max(abs(h))); 

Pass reference signal through a filter. Add delay and noise.

rxSignal = awgn([zeros(213,1);filter(h,1,txSignal)], ...
           70,"measured");
 

With the WindowLength property equal to the default value, the estimated timing offset points to the largest peak in the channel impulse response. But just using the default value for window length may not provide the timing offset required for reducing ISI. With the WindowLength=cplen+1, the function focuses on a window that is the length of the cyclic prefix (cplen) plus one sample. Then estimated timing offset shifts as much energy of the channel impulse response as possible into the cyclic prefix region of an OFDM symbol, aligning the timing offset with the received signal and reducing the ISI.

windowLenVec = [1 (cplen+1)];
 for k = 1:length(windowLenVec)
    % Get timing estimate
    offset = timingEstimate(rxSignal,refSig,WindowLength=windowLenVec(k));
    % Demodulate signal
    rxofdmData = ofdmdemod(rxSignal(offset+(1:symLen*numSym)), ...
                 nfft,cplen,cplen,nullIdx).';
    % Find the best possible equalizer by using
    % known data
    equalizerCoef = zeros(numDataCarrs,1);
     for n = 1:numDataCarrs
         equalizerCoef(n) = rxofdmData(:,n)\(ofdmData(n,1+(1:numSym)).');
     end
    % Equalize signal
    eqData = rxofdmData*diag(equalizerCoef);
    % Plot constellation diagram for all subcarriers
    % Set WindowLength=cplen+1 leads to a timing estimate that reduces ISI
    constdiag{k} = comm.ConstellationDiagram(ShowReferenceConstellation=false);
    constdiag{k}.Title = ['WindowLength = ' num2str(windowLenVec(k))...
                          ', Offset = ' num2str(offset)];
    constdiag{k}(eqData(:));
  end

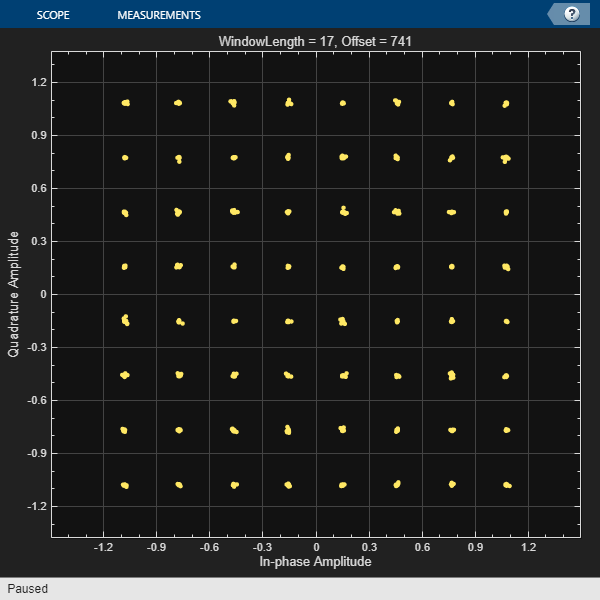
Restore the random seed.

  rng(s); 

Input Arguments

waveform — Input waveform

T-by-N_r matrix

Input waveform, specified as a T-by-N_r matrix where:

• T is the number of time domain samples.

• N_r is the number of receive antennas.

Data Types: double | single

refsig — Reference signal

L-by-N_t matrix

Reference signal, specified as an L-by-N_t matrix where:

• L is the number of time domain samples.

• N_t is the number of transmit streams.

Data Types: double | single

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: Z = timingEstimate(Y,M,Threshold=0.2);

Threshold — Detection threshold

0.2 (default) | real scalar between 0 and 1

Detection threshold, specified as a real scalar between 0 and 1. If any normalized cross-correlation magnitude is equal to or greater than this threshold, the function decides that the reference signal is in the waveform.

Data Types: single | double

WindowLength — Window length of consecutive samples

1 (default) | positive integer | ...

Window length of consecutive samples, specified as a positive integer.

Data Types: single | double

Output Arguments

offset — Estimated timing offset

scalar integer | empty array

Estimated timing offset, returned as an integer, given by an integer number of samples relative to the first sample of the input waveform.

• If the offset is nonnegative, waveform(offset+(1:L),:) is a good match to the reference signal.

• If offset is negative, the received waveform is late late. waveform(1:(L+offset),:) is a good match to refsig(1-offset:L,:).

• If waveform is not a good match to refsig, offset is an empty array.

normcorr — Normalized correlation magnitude

(T+L-1)-by-N_r-by-N_t array

Normalized correlation magnitude, returned as a (T+L-1)-by-N_r-by-N_t array. Each element in the array is a real value in the range [0,1]. A larger value indicates a stronger correlation between the input waveform and the reference signal for the corresponding offset, receive antenna, and the transmit stream.

• The function returns an empty array for offset, if all values in normcorr are less than the default threshold of 0.2.

• The function calculates offset from the Nt*Nr estimated channel impulse responses between the transmit streams and the receive antennas, if normcorr meets or exceeds the default threshold value.

Algorithms

The timing offset indicates the estimated location of a reference signal in the received signal, if the reference signal is present in the received signal. The timingEstimate function helps to calculate this offset. This function has two key stages. The first stage decides whether the reference signal is in the received waveform. If the reference signal is in the received waveform, then the second stage estimates the timing offset.

Both algorithms the function uses are based on cross-correlating the reference signal and the received waveform.

Stage 1: Detection Stage

The detection algorithm uses the principle of a matched filter or cross-correlator to detect the presence and location of a reference signal within a received waveform. In cross-correlation, you slide a reference or given signal across a received signal and calculate the similarity between the signal. If you plot this on a graph, the peaks in the cross-correlated signal indicate potential locations of the reference signal within the received signal at a particular time. The higher the peak the more the similarity between the reference signal and the received signal. Several factors influence the magnitude of the cross-correlation peaks. These factors could be the energy of the reference signal, the energy of the received signal, and the noise level, to name a few. You can normalize or scale the peaks for a more accurate detection of the given signal. Without appropriate scaling, it becomes harder to compare the correlation peaks, which in turn makes the detection more difficult or inaccurate.

Consider this:

refSignal = 2.3*randn(256,1,'like',1j); % No need to have unit power

% Create the waveform by concatenating zeros, scaled reference signals, and more zeros
waveform = [zeros(12,1);2*refSignal;zeros(45,1);0.2*refSignal];

% Add complex Gaussian noise to the waveform
waveform = waveform + 0.01*randn(size(waveform),'like',1j);

% Perform correlation by filtering the waveform with a flipped and conjugated reference signal
corrResult = filter(conj(flipud(refSignal)),1,waveform;zeros(length(refSignal)-1,1)]); 
% Equivalent to xcorr(waveform,refSignal), without padded zeros

% Plot the absolute value of the correlation result
figure(1)
plot(abs(corrResult))

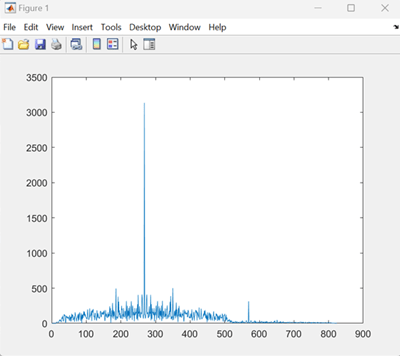
The peak in graph corresponding to 0.2*refSignal is small compared to the peak corresponding to 2*refSignal. The difference here are the scaling values : 0.2 and 2. You also need to calculate the correlation result appropriately if there are no known scaling values.

To remove the effects of scaling factors 0.2 and 2, you can use the fact that for any column vectors u and v, abs(u'*v)/sqrt((u'*u)*(v'*v)) is always between 0 and 1 In this scenario, u is refSignal and v is a moving slice of waveform. Compute and store the magnitude squared of the waveform using a sliding window. Normalize the correlation magnitude to get two peaks very close to 1.

% Calculate the magnitude squared of the waveform using a sliding window
waveformMagSq = filter(ones(size(refSignal)),1,[real(waveform.*conj(waveform)); zeros(length(refSignal)-1, 1)]);
% Calculate the power of the reference signal
refSigPower = real(refSignal'*refSignal);

% Normalize the correlation magnitude
normCorrMag = abs(corrResult) ./ sqrt(waveformMagSq * refSigPower);

% Create a new figure for plotting
figure(2)

% Plot the normalized correlation magnitude
plot(normCorrMag)

The timingEstimate function uses the above algorithm. The function normalizes the correlation magnitude for each waveform from each receive antenna (1:R) and each reference signal from each transmit layer (1:P).

If one such normalization vector has a value that is equal to or greater than the detection threshold, then the function decides that the reference signal is present in the received waveform. To understand more about detection threshold, see Estimate Timing Offset of QPSK Signals.

Estimating Timing Offset

After confirming the presence of the reference signal in the received waveform, you need to estimate the timing offset You can use the autocorrelation properties of the reference signal to estimate the timing offset. Consider this example:

Generate a complex Gaussian noise reference signal with a specified scale factor. The scale factor of 3.4 is arbitrary and does not need to represent unit power.

refSignal = 3.4*randn(256,1,'like',1j);

Calculate the total energy of the reference signal by taking the conjugate transpose of the signal.

refTotalEnergy = real(refSignal'*refSignal);

Simulate the effect of the channel on the reference signal by filtering it with a given channel impulse response. The filter coefficients [0.8 0.5+0.2j -0.3+0.4j] represent the channel.

waveform = filter([0.8 0.5+0.2j -0.3+0.4j], 1, refSignal);

Add complex Gaussian noise to the waveform to simulate a noisy channel. The noise has a standard deviation of 0.01, scaled by the waveform's size.

waveform = waveform + 0.01*randn(size(waveform), 'like', 1j);

Perform cross-correlation between the received waveform and the reference signal. For this, filter the received waveform with the time-reversed and conjugated reference signal. The result is equivalent to the cross-correlation function without padding zeros at the end.

corrResult = filter(conj(flipud(refSignal)), 1, [waveform;zeros(length(refSignal)-1, 1)]);

Estimate the channel impulse response by normalizing the cross-correlation result with the total energy of the reference signal.

estImpulseResponse = corrResult / refTotalEnergy;

Extract the estimated channel impulse response starting from the sample immediately after the reference signal length. This portion of the impulse response should be close to the actual channel filter coefficients. Add the length of the reference signal to the index to account for the delay introduced by the filtering process.

estImpulseResponse(length(refSignal)+(0:2))

Expected to be close to [0.8; 0.5+0.2j; -0.3+0.4j]

In the above example, the computation assumes that the reference signal has good autocorrelation properties or the autocorrelation function is close to an impulse, and that the reference signal is present in the received waveform.

The timingEstimate function calculates estimated impulse response for each waveform from each receive antenna (1:R) and each reference signal from each transmit layer (1:P), and then the function sums the magnitude squared of the estimated impulse response over all R*P combinations.

The function uses this vector of total power to find which W consecutive samples in this vector have the largest sum. Here, W is the width of the window used to sum the power of estimated impulse response components. Subtracting the length of the reference signal from the one-based index of the first sample in these W consecutive samples gives the timing estimate. (If more than one sets of W consecutive samples achieve the largest sum, then smallest timing estimate is used.)

• If W= 1, the algorithm looks for a single peak in the total power vector.

• If W>1, the algorithm considers a peak energy that spreads over multiple samples instead of one sample. You can set W to CPLEN+1, where CPLEN is the cyclic prefix length of an OFDM symbol. This is the potential region of the start of the OFDM symbol. This algorithm is a heuristic to reduce intersymbol interference.

This algorithm provides a practical means to estimate the timing offset in a communication system by leveraging the autocorrelation properties of a reference signal and the received waveform's cross-correlation with it.

Version History

Introduced in R2024a