PN Sequence Generator
Generate pseudonoise sequence
Libraries:
Communications Toolbox /
Comm Sources /
Sequence Generators
Communications Toolbox HDL Support /
Comm Sources
Description
The PN Sequence Generator block generates a sequence of pseudorandom binary numbers using a linear-feedback shift register (LFSR). Pseudonoise sequences are typically used for pseudorandom scrambling, and in direct-sequence spread-spectrum systems. For more information, see More About.
These icons shows the block with all ports enabled.
![]()
![]()
Examples
Sequences output from the PN Sequence Generator block can be modeled using a linear feedback shift register (LFSR) built with primitive Simulink® blocks.

The cm_ex__pnseq_vs_prim_sl model generates the generator polynomial, p(z)=z^6+z+1, by using the PN Sequence Generator block and by modeling an LFSR using primitive Simulink blocks. The discrete block LFSR schematic model interprets the Initial states and Output mask vector (or scalar shift value) parameters of the PN Sequence Generator block. The PreLoadFcn callback function initializes runtime parameters. To view the callback functions from the Simulink Toolstrip, on the Modeling tab, in the Design gallery, click Property Inspector.
The scope output shows that the two implementations produce matching PN sequences.

Using the PN Sequence Generator block allows you to easily generate PN sequences of large periods. To experiment further, open the model. Modify settings to see how the performance varies for different path delays or adjust the PN sequence generator parameters. You can experiment with different initial states by changing the value of Initial states before running the simulation. For all values, the two generated sequences are the same.
Digital communications systems commonly use additive scrambling and descrambling to randomize input data to aid in timing synchronization and meeting power spectral requirements. The Scrambler block supports multiplicative scrambling but does not support additive scrambling. To perform additive scrambling, you can use the PN Sequence Generator block. This example implements the additive scrambling specified in IEEE 802.11™ [1] by scrambling input data with an output sequence generated by the PN Sequence Generator block. For a MATLAB® example with a similar workflow, see the Additive Scrambling of Input Data example on the comm.PNSequence reference page.
This figure shows an additive scrambler, that uses the generator polynomial 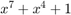 , as specified in Figure 17-7 of IEEE 802.11™ Section 17.3.5.5 [1].
, as specified in Figure 17-7 of IEEE 802.11™ Section 17.3.5.5 [1].

Compare the shift register specified in 802.11 with the shift register implemented using a PN Sequence Generator block and observe the two shift register schematics are mirror images of each other. Therefore, when configuring the PN Sequence Generator block to implement an additive scrambler, you must reverse values for the generator polynomial, the initial states, and the mask output. To take the output of the register from the leading end, specify a shift value of 7.

For more information about the 802.11 scrambler, see [1] and the wlanScramble (WLAN Toolbox) reference page.
The cm_additive_scrambling model scrambles and compares the generated scrambling sequence and a frame of data scrambled according to the 802.11 specified additive scrambler by using these two additive scrambler implementations:
A shift register comprised of discrete Delay (Simulink) blocks and Logical Operator (Simulink) blocks configured as XOR operators.
The PN Sequence Generator block and XOR operator.

To compare the additive scrambler implementations, the cm_additive_scrambling model uses:
A Bernoulli Binary Generator block to provide an input signal to scramble.
A PN Sequence Generator block configured to use
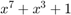 for the generator polynomial, [1 1 1 1 1 1 1] for the initial shift register state, and 7 for the output scrambling shift value.
for the generator polynomial, [1 1 1 1 1 1 1] for the initial shift register state, and 7 for the output scrambling shift value.A Logical Operator (Simulink) block configured as an XOR operator to apply the scramble sequence to the input data.
An Error Rate Calculation block to verify the scrambled data output from the discrete block shift register and the PN sequence versions of the additive scrambler match.
The
PreLoadFcncallback function to create a workspace variable containing the 127-bit scrambler output sequence specified in section 17.3.5.5 of the IEEE 802.11 standard. A Relational Operator (Simulink) configured for an==operation compares the 127-bit scrambler sequence as output from the Signal From Workspace block to the PN Sequence block output.
Simulate Additive Scrambling
Run the model and display the results of the error rate calculation for the scrambled input sequence and equal comparison for the scrambler sequence.
Number of errors in scrambled output comparison is 0. Number of mismatches comparing PN sequence output to IEEE 802.11 scrambler sequence 0.
References
[1] IEEE Std 802.11™-2020 (Revision of IEEE Std 802.11-2016). "Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications." IEEE Standard for Information technology - Telecommunications and information exchange between systems. Local and metropolitan area networks - Specific requirements.
This model simulates pseudo-random spreading for a single-user system in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently by using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.
The model uses random binary data, which is BPSK modulated (real), spread by PN sequences, and then transmitted over a multipath AWGN channel. The receiver consists of a despreader, a diversity combiner, and a BPSK demodulator. The receiver achieves gains from diversity combining due to the ideal auto-correlation properties of the PN sequences used when spreading the data.

To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or adjust the PN sequence generator parameters.
This model simulates pseudo-random spreading for two users in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.
The model uses random binary data, which is BPSK modulated (real), spread by PN sequences, and then transmitted over a multipath AWGN channel. The receiver consists of a despreader, a diversity combiner, and a BPSK demodulator.

Using the same transmission data, the model calculates the performance for two-user transmissions through identically configured, multipath AWGN channels.
Because the transmissions for the individual users were spread using different PN sequences, the error rate computed for the users are different. Due to the higher cross-correlation properties of the nonorthogonal PN sequences used to spread the data, BER performance is degraded in a multipath environment. Sequences with high orthogonality, such as Hadamard and Kasami, are a better choice for multipath environments. For a multipath example that uses Hadamard code sequences when spreading user data, see Orthogonal Spreading for Multiuser System in Single-Path Channel. For a multipath example that uses Kasami code sequences when spreading user data, see Kasami Spreading for Multiuser System in Multipath Channel.
To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or with different PN sequences for the individual users.
Ports
Input
Output mask to delay the PN sequence from initial time, specified as a binary vector with N elements. N is the degree of the generator polynomial.
Dependencies
To enable this port, set Output mask
source to Input port.
Data Types: double | uint8 | ufix1
Output size for variable-size output signals, specified as an integer. For information about variable-size signals, see Variable-Size Signal Basics (Simulink).
Dependencies
To enable this port, select Output
variable-size signals and set Maximum
output size source to Dialog
parameter.
Data Types: double
Reference input, specified as a column vector that determines the maximum and current output sequence length. The Ref input must be a variable-size signal. For information about variable-size signals, see Variable-Size Signal Basics (Simulink).
Dependencies
To enable this port, select Output
variable-size signals and set Maximum
output size source to Inherit from reference
input.
Data Types: double
Reset sequence generator, specified as 0 or
1. For more information, see Reset Behavior.
Dependencies
To enable this port, select Reset on nonzero input.
Data Types: Boolean
Output
PN sequence, returned as a binary vector. The data type of the output is specified by Output data type.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Generator polynomial that determines the feedback connections of the shift register, specified as one of these options:
Character vector or string scalar of a polynomial whose constant term is
1. For more information, see Representation of Polynomials in Communications Toolbox.Binary-valued row vector that represents the coefficients of the polynomial in order of descending powers. The length of this vector must be N + 1, where N is the degree of the polynomial. The first and last entries must be
1, indicating the leading term with degree N and a constant term of 1.Integer-valued row vector of elements that represent the exponents for the nonzero terms of the polynomial in order of descending powers. The last entry must be
0, indicating a constant term of 1.
For more information, see Simple Shift Register Generator and Polynomial Order and Shift Register Orientation.
Example: 'z^8 + z^2 + 1', [1 0 0 0 0 0 1 0 1],
and [8 2 0] represent the same polynomial,
p(z) = z
8 + z
2 + 1.
Initial shift register states of the PN sequence generator when the simulation starts, specified as a binary-valued row vector. The length of the vector must equal the degree of the generator polynomial specified by the Generator polynomial. For more information, see Simple Shift Register Generator and Polynomial Order and Shift Register Orientation.
Note
For the block to generate a nonzero sequence, the Initial states vector must contain at least one nonzero element.
Output mask source that indicates how the output mask information is given to the block, specified as one of these:
Dialog parameterto use theOutput mask vector (or scalar shift value)parameter setting.Input portto add and use theMaskinput port.
Output mask vector or scalar shift value, specified as an integer scalar or binary row vector of length N, where N is the degree of the generator polynomial. This parameter determines the delay of the PN sequence from the initial time. For more information, see Shifting PN Sequence Starting Point.
Dependencies
To enable this parameter, set Output mask
source to Dialog parameter.
Select this parameter to enable variable-length output sequences during simulation. When you clear this parameter, the block outputs fixed-length sequences. When you select this parameter, the block can output variable-length sequences. For information about variable-size signals, see Variable-Size Signal Basics (Simulink).
Positive scalars specify the time in seconds between each
sample of the output signal. If you set the sample time to -1, the output
signal inherits the sample time from downstream. For information on the relationship between the
Sample time and Samples per frame parameters,
see
Sample Timing.
Example: 1 specifies a sample time of 1 second.
Dependencies
To enable this parameter, clear Output variable-size signals.
Samples per frame in one channel of the output signal, specified as a positive integer. For information on the relationship between Sample time and Samples per frame, see Sample Timing.
Dependencies
To enable this parameter, clear Output variable-size signals.
Select how to specify the maximum sequence output size.
Dialog parameter— Select this value to configure the block to use the Maximum output size parameter setting as the maximum permitted output sequence length. The oSiz input port specifies the current size of the output signal, and the block output inherits the sample time from the input signal. The input value of oSiz must be less than or equal to the Maximum output size parameter.Inherit from reference port— Select this value to enable the Ref input port and configure the block to inherit the sample time, maximum size, and current output size from the variable-sized signal at the Ref input port. These set the maximum permitted output sequence length.
Dependencies
To enable this parameter, select Output variable-size signals.
Specify the maximum output size for the block. n is a positive scalar.
Example: [10 1] specifies a 10-by-1 maximum size for the output
signal.
Dependencies
To enable this parameter, select Output variable-size
signals and set Maximum output size source to
Dialog parameter.
Select this parameter to add the Rst input port. For more
information, see Reset Behavior.
Select this parameter to make the Number of packed bits and Interpret bit-packed values as signed parameters available.
When this parameter is selected, the block generates (M×P) bits. M is the number of samples per frame specified in the Samples per frame parameter. P is the size of the bit-packed words specified in the Number of packed bits parameter. Each group of P bits is packed into an integer, resulting in an integer-valued output vector containing M elements. The data type of the output is specified by Output data type.
Note
For the integer representation, the top-most bit in each group of P bits is considered the MSB, while the bottom-most bit is the LSB.
Number of packed bits, specified as an integer in the range [1, 32].
Dependencies
To enable this parameter, select Enable bit-packed outputs.
Interpret bit-packed values as signed integer data values when selected or unsigned integer data values when cleared. When selected, a 1 in the most significant bit (sign bit) indicates a negative value.
Dependencies
To enable this parameter, select Enable bit-packed outputs.
Output data type, specified as double,
boolean, or Smallest unsigned
integer.
When Enable bit-packed outputs is cleared, the output data type can be specified as a
double,boolean, orSmallest unsigned integer. When the Output data type parameter is set toSmallest unsigned integer, the output data type is selected based on the settings used in the Hardware Implementation pane of the Configuration Parameters dialog box of the model. IfASIC/FPGAis selected in the Hardware Implementation pane, the output data typeufix(1)= ideal minimum one-bit size. For all other selections, it is an unsigned integer with the smallest available word length large enough to fit one bit, usually corresponding to the size of a char (for example,uint8).When Enable bit-packed outputs is selected, the output data type can be specified as
doubleorSmallest unsigned integer. When the Output data type parameter is set toSmallest unsigned integer, the output data type is selected based on the Interpret bit-packed values as signed and Number of packed bits parameters, and the settings used in the Hardware Implementation pane of the Configuration Parameters dialog box of the model. IfASIC/FPGAis selected in the Hardware Implementation pane, the output data type is the ideal minimum n-bit size, such assfix(n)orufix(n), based on the Interpret bit-packed values as signed parameter. For all other selections, it is a signed or unsigned integer with the smallest available word length large enough to fit n bits.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
A linear-feedback shift register (LFSR), implemented as a simple shift register generator (SSRG), is used to generate PN sequences. This type of shift register is also known as a Fibonacci implementation.

The polynomial g determines the feedback connections of the shift register. It is a primitive binary polynomial in z, grzr+gr–1zr–1+gr–2zr–2+...+g0. For the coefficient gk=0 to r, the coefficient gk is 1 if there is a connection from the kth register to the adder. The leading term, gr, and the constant term, g0, of the generator polynomial must be 1 because the polynomial must be primitive. At each time step, all r registers in the generator update their values according to the value of the incoming arrow to the shift register. The adders perform addition modulo 2. The output of the LFSR reflects the sum of all connections in the m mask vector.
g is specified by the Generator polynomial parameter.
The initial value of r is specified by the Initial states parameter.
m determines the shift of the PN sequence starting point and is specified by the Output mask vector (or scalar shift value) parameter or Mask port.
This table indicates two sets of parameter values that correspond to the generator polynomial g(z) = z8 + z2 + 1.
| Quantity | Example 1 | Example 2 |
|---|---|---|
| g | g1 = [1 0 0 0 0 0 1 0 1] | g2 = [8 2 0] |
| Degree of generator polynomial, g | 8, which is length(g1)-1
| 8 |
| Initial states | [1 0 0 0 0 0 1 0] | [1 0 0 0 0 0 1 0] |
For an example, see Model PN Sequence Generation with Linear Feedback Shift Register.
The implementation orients shift registers from left to right with the generator polynomial (g), initial states, and mask output defined in descending order. Specifically grzr+gr–1zr–1+gr–2zr–2+...+g0.
When attempting to model and match results from literature, you must recognize whether your source uses the same convention or the mirror image of this convention and is defined in ascending order.
For an example, see Additive Scrambling of Input Data in Simulink.
To shift the starting point of the PN sequence, specify the Output mask vector (or scalar shift value) parameter as:
An integer representing the length of the shift.
The default Output mask vector (or scalar shift value) setting of 0 corresponds to no shift. As illustrated in the LFSR shift register diagram in Simple Shift Register Generator, there is no shift when the only connection is along the arrow labeled m0.
This table shows the shift that occurs when you set Output mask vector (or scalar shift value) to 0 versus a positive integer d.
T = 0 T = 1 T = 2 ... T = d T = d+1 Shift = 0 x0 x1 x2 ... xd xd+1 Shift = d xd xd+1 xd+2 ... x2d x2d+1 A binary vector whose length is equal to the degree of the generator polynomial. The LFSR shift register diagram in Simple Shift Register Generator shows Output mask vector (or scalar shift value) specified as a mask vector, m. The binary vector must have N elements, where N is the degree of the generator polynomial. To calculate the mask vector, use the
shift2maskfunction.The binary vector corresponds to a polynomial in z, mr–1zr–1 + mr–2zr–2 + ... + m1z + m0, of degree at most r–1. The mask vector that correspond to a shift of d is the vector that represents m(z) = zd modulo g(z), where g(z) is the generator polynomial.
For example, if the degree of the generator polynomial is 4, then the mask vector that corresponds to d = 2 is
[0 1 0 0], which represents the polynomial m(z) = z2.
Before you can reset the generator sequence, you must select the
Reset on nonzero input parameter to enable the
Rst input port. Suppose that the PN Sequence Generator block outputs
[1 0 0 1 1 0 1 1] when no reset exists. This table shows the effect
on the PN Sequence Generator block output for the parameter values indicated.
| Reset Signal | Reset Signal Settings | PN Sequence Generator block | Reset Signal and Output Signal |
|---|---|---|---|
| No reset |
|
|
|
| Scalar reset signal |
|
|
|
| Vector reset signal |
|
|
For the no-reset case, the block outputs the sequence without resetting it.
For the scalar and vector reset signal cases, the block inputs the reset signal [0
0 0 1 0 0 0 0] to the Rst port. Because the fourth bit of
the reset signal is a 1 and Sample time is
1, the block resets the sequence output at the fourth bit.
For variable-sized outputs, the block supports only scalar reset signal inputs.
To generate a maximum length sequence for a generator polynomial that has the degree r, set Generator polynomial to a value from the following table. The maximum sequence length is 2r – 1.
| r | Generator Polynomial | r | Generator Polynomial | r | Generator Polynomial | r | Generator Polynomial |
|---|---|---|---|---|---|---|---|
| 2 | [2 1 0] | 15 | [15 14 0] | 28 | [28 25 0] | 41 | [41 3 0] |
| 3 | [3 2 0] | 16 | [16 15 13 4 0] | 29 | [29 27 0] | 42 | [42 23 22 1 0] |
| 4 | [4 3 0] | 17 | [17 14 0] | 30 | [30 29 28 7 0] | 43 | [43 6 4 3 0] |
| 5 | [5 3 0] | 18 | [18 11 0] | 31 | [31 28 0] | 44 | [44 6 5 2 0] |
| 6 | [6 5 0] | 19 | [19 18 17 14 0] | 32 | [32 31 30 10 0 | 45 | [45 4 3 1 0] |
| 7 | [7 6 0] | 20 | [20 17 0] | 33 | [33 20 0] | 46 | [46 21 10 1 0] |
| 8 | [8 6 5 4 0] | 21 | [21 19 0] | 34 | [34 15 14 1 0] | 47 | [47 14 0] |
| 9 | [9 5 0] | 22 | [22 21 0] | 35 | [35 2 0] | 48 | [48 28 27 1 0] |
| 10 | [10 7 0] | 23 | [23 18 0] | 36 | [36 11 0] | 49 | [49 9 0] |
| 11 | [11 9 0] | 24 | [24 23 22 17 0] | 37 | [37 12 10 2 0] | 50 | [50 4 3 2 0] |
| 12 | [12 11 8 6 0] | 25 | [25 22 0] | 38 | [38 6 5 1 0] | 51 | [51 6 3 1 0] |
| 13 | [13 12 10 9 0] | 26 | [26 25 24 20 0] | 39 | [39 8 0] | 52 | [52 3 0] |
| 14 | [14 13 8 4 0] | 27 | [27 26 25 22 0] | 40 | [40 5 4 3 0] | 53 | [53 6 2 1 0] |
For more information about the shift-register configurations that these polynomials represent, see Digital Communications by John Proakis [1].
The time between output updates is equal to the product of the
Samples per frame and Sample time parameter
values. For example, if Sample time and Samples per
frame each equal 1, the block outputs one sample every
second. If you increase Samples per frame to 10, then the block outputs
a 10-by-1 vector every 10 seconds. This timing ensures that the equivalent output rate is
not dependent on the Samples per frame parameter.
References
[1] Proakis, John G. Digital Communications. 5th ed. New York: McGraw Hill, 2007.
[2] Lee, J. S., and L. E. Miller. CDMA Systems Engineering Handbook. Boston and London. Artech House, 1998.
[3] Golomb, S.W. Shift Register Sequences. Laguna Hills. Aegean Park Press, 1967.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block has one default HDL architecture.
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
You can select
Input portas the Output mask source on the block. In this case, theMaskinput signal must be a vector of data typeufix1.If you select Reset on nonzero input, the input to the
Rstport must have data typeBoolean.Outputs of type
doubleare not supported for HDL code generation. All other output types (including bit-packed outputs) are supported.You cannot generate HDL for this block inside a Resettable Synchronous Subsystem (HDL Coder).
You cannot generate HDL for this block inside a Triggered Subsystem if the Use trigger signal as clock option is selected. See Using Triggered Subsystems for HDL Code Generation (HDL Coder).
Version History
Introduced before R2006aStarting in R2020a, Simulink no longer allows you to use the PN Sequence Generator block version available before R2015b.
Existing models automatically update to load the PN Sequence Generator block version announced in Source blocks output frames of contiguous time samples but do not use frame attribute. For more information on block forwarding, see Maintain Compatibility of Library Blocks Using Forwarding Tables (Simulink).
See Also
Blocks
Objects
Topics
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)