I/Q Imbalance
Apply I/Q imbalances to complex signal
Libraries:
Communications Toolbox /
RF Impairments and Components
Description
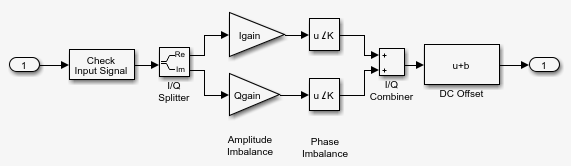
The I/Q Imbalance block applies in-phase and quadrature imbalances to a complex signal. This block applies an amplitude imbalance, a phase imbalance, and a DC offset to the in-phase and quadrature signal components. For more information, see I/Q Imbalance Implementation and Algorithms.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
Algorithms
The I/Q amplitude imbalance, I/Q phase imbalance, and DC offset impairments are described sequentially in the section.
For an I/Q amplitude imbalance, Ia, the impairment is applied to the input signal, xr+ jxi and y AmplitudeImbalance is an intermediate output.
y AmplitudeImbalance y rAmplitudeImbalance + jyiAmplitudeImbalance
y AmplitudeImbalance =
For an I/Q phase imbalance, Ip, the impairment is applied to y AmplitudeImbalance and yPhaseImbalance is an intermediate output.
yPhaseImbalance yrPhaseImbalance + jyiPhaseImbalance
yPhaseImbalance =
For DC offsets, IDC and QDC, the impairment is applied to y PhaseImbalance and y is the final output.
y = (yrPhaseImbalance + IDC) + j(yiPhaseImbalance + QDC)
Variables for these calculations are defined in this list.
I a is the I/Q amplitude imbalance.
Ip is the I/Q phase imbalance.
IDC is the in-phase DC offset.
QDC is the quadrature DC offset.
x is the complex input signal and is given by xr + jxi.
xr and xi are the real and imaginary parts, respectively, of x.
y is the complex output signal and is given by yr + jyi.
yr and yi are the real and imaginary parts, respectively, of y.
Extended Capabilities
Version History
Introduced before R2006a
See Also
Blocks
- I/Q Compensator Coefficient to Imbalance | I/Q Imbalance Compensator | Free Space Path Loss | Memoryless Nonlinearity | Phase Noise | Receiver Thermal Noise