パルス幅変調とは?
PWMとは、Pulse Width Modulationの略でパルス幅変調とも言います。特定の矩形波パルスを使用して電気機器への電力を効率よく制御するための一般的な技術です。
PWM信号は、主に半導体の通電/非通電のデューティ比(ON/OFFとなる時間の割合)を制御するために利用されます。モーター制御では、主にインバータ回路で使われており、PMW信号のデューティ比や周波数を変えることでモーター駆動に最適な正弦波(sin波)交流電圧を擬似的に作成します。このPWM信号を適切に行うことで、モーターの効率と制御性能を向上させることが出来ます。
デューティ比
デューティ比とは、ある周期的な方形波におけるオンの期間(振幅がゼロでない期間)の割合をいいます。
\(デューティ比(D) = {オン期間 \over 周期T}\)

PWM出力によるデューティ比
この比率を変化させることで、平均出力を調節します。
例えば電気回路で良く使われるチョッパー回路では、入力の直流電源に対し、半導体のスイッチング信号をPWM信号で指示することで、平均電圧(Vout)を制御します。
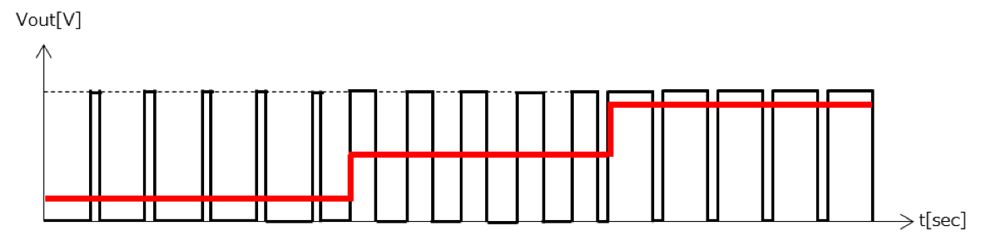
PWM出力による平均電圧
さらにデューティ比を、より細かく制御すると、以下のような擬似正弦波を表現することが出来ます。
これにより、3相交流モーターの制御で使用する正弦波信号を作り出すことが出来ます。
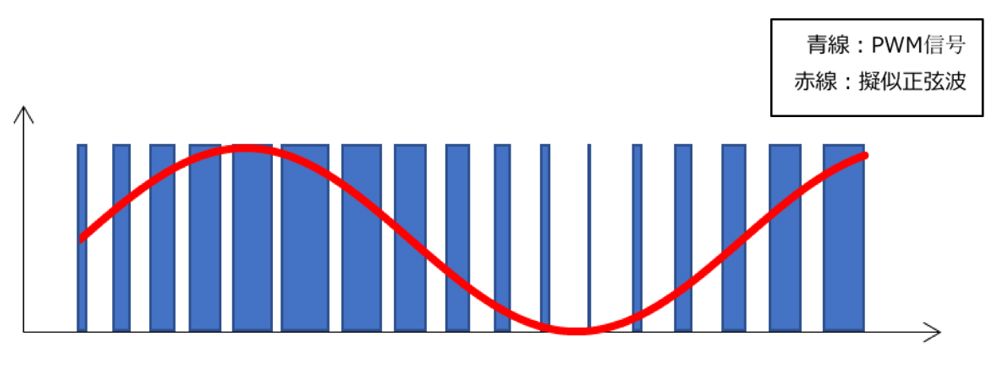
PWM出力による擬似正弦波
PWM信号の作成方法は、幾つかありますが、代表的な例として、のこぎり波を用いた作り方を示します。
比較基準値\((Vs)\)と比較対象の信号\((Vc)\)の大きさを、以下のような条件で比較して出力を決定することで
大きさ1と0の値で構成されるパルス信号(PWM信号)を作成することが出来ます。
また、基準値を変化させることでPWMのデューティ比が変化します。
条件
\(\begin{cases} Vc>Vsの時:1を出力\\ Vc>Vsの時:0を出力\end{cases} \)
\((Vc:のこぎり波による搬送波 / Vs:基準値)\)

のこぎり波を使ったPWM信号作成
PWMの活用例
スイッチング・レギュレータ
スイッチング・レギュレータとは、直流電圧を任意の直流電圧に変換して出力する電源装置で、DC/DCコンバータを実現する方式の1つです。出力電圧を監視しながら半導体のスイッチング素子をPWM制御(オン/オフ時間)することで、入力直流電圧を希望する出力直流電圧に変換します。
スイッチング・レギュレータの種類は主に3つに分類できます。
- 降圧型(バック):出力電圧を入力電圧よりも下げる方式
- 昇圧型(ブースト):出力電圧を入力電圧よりも上げる方式
- 昇降圧型(バック・ブースト):上記2つのどちらも対応できる方式
スイッチング・レギュレータの最大の利点は、高い変換効率が得られる点です。およそ80%~98%と高い変換効率が得られると言われます。
次に、昇圧型と降圧型の基本回路図と、どこでPWM制御が使われているかを示します。
- 降圧コンバータ
[関係式]
出力電圧は、次の式によって定義されます。
\(Vout = D × Vin\)
\((※D:PWMのデューティ比)\)
[回路モデル]
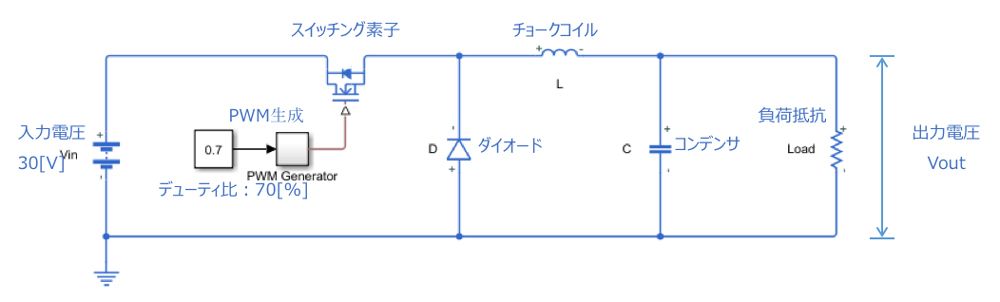
降圧コンバータの回路モデル
[結果]
\(Vout:0.7 × 30 = 21[V] \)
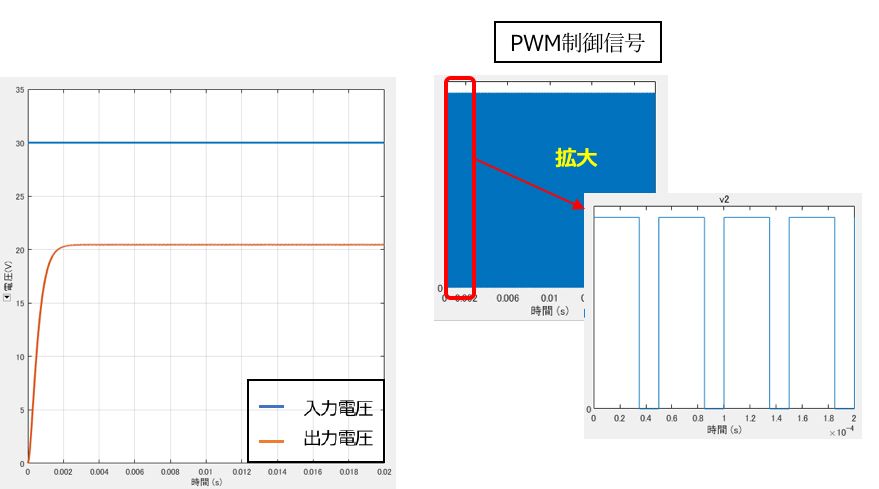
降圧コンバータのシミュレーション結果(入出力電圧とPWM制御信号)
- 昇圧コンバータ
[関係式]
出力電圧は、次の式によって定義されます。
\(Vout = {Vin \over (1-D)}\)
\((※D:PWMのデューティ比) \)
[回路モデル]

昇圧コンバータの回路モデル
[結果]
\(Vout = {30 \over Y1 - 0.5Y}=60[V]\)

昇圧コンバータのシミュレーション結果(入出力電圧とPWM制御信号)
- 昇降圧型コンバータ
反転トポロジと非反転トポロジを使用した昇降圧コンバータを示します。- 反転トポロジ
\(Vout = -{D \over (1-D)}*Vin\)
\((※D:PWMのデューティ比)\)
[関係式]
出力電圧は、次の式によって定義されます。
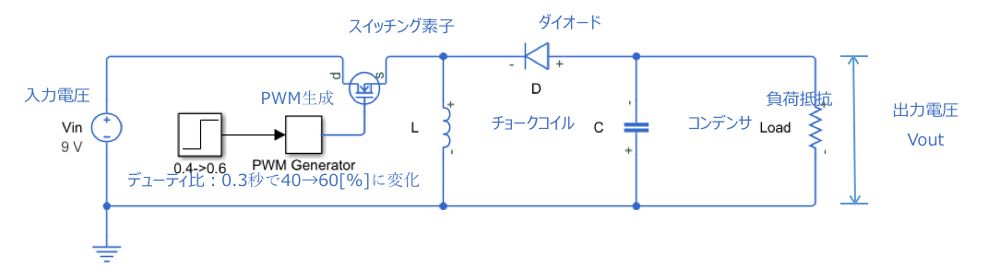
昇降圧コンバータの回路モデル(反転トポロジ)
\(\begin{cases} (Vout1(0-0.3秒):-{0.4 \over (1-0.4) ) }×9 =-6[V]\\ Vout2(0.3-0.7秒) : -{0.6 \over (1-0.6) ) }×9 =-13.5[V]\end{cases}\)
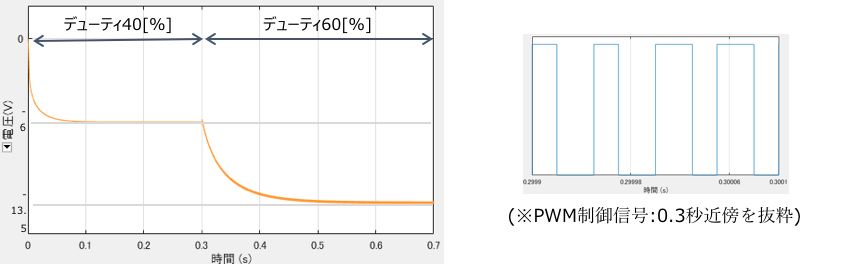
昇降圧コンバータ(反転トポロジ)のシミュレーション結果(出力電圧とPWM制御信号)
- 非反転トポロジ
[関係式]
出力電圧は、次の式によって定義されます。
\(Vout = {D \over (1-D)}×Vin\)
\((※D:PWMのデューティ比)\)
[回路モデル]

昇降圧コンバータ(非反転トポロジ)の回路モデル
/(\begin{cases} (Vout1(0-0.1秒)):{0.4 \over (1-0.4) ) }×9 =6[V]\\ Vout2(0.1-0.2秒) : {0.6 \over (1-0.6) ) }×9 =13.5[V]\end{cases} \)

昇降圧コンバータ(非反転トポロジ)のシミュレーション結果(入出力電圧とPWM制御信号)
[補足]
レギュレータとは、出力する電圧・電流を一定にするように制御する回路を指します。
回路の構成の違いにより、リニア・レギュレータとスイッチング・レギュレータがあります。
スイッチング・レギュレータは先に述べた通りでPWM信号を使用して出力電圧制御をします。
対してリニア・レギュレータは、可変抵抗を変化させることで出力電圧を制御します。ただ、変換効率の観点から言うと、およそ60%の変換効率しか得られないと言われます。その分、回路構成が簡単でコストが抑えられるというメリットはあります。
| 分類(レギュレータ) | 制御方式 | メリット | デメリット |
| スイッチング方式 | PWM信号を使用して出力電圧を制御 | 変換効率が良い (80%~98%) |
回路が複雑になり易い コストが高い |
| リニア方式 | 回路構成が簡単 コストが低い |
回路構成が簡単 コストが低い |
変換効率が低い 約60%前後 |
MATLAB環境によるDC/DCコンバータの制御開発
MATLAB®環境を活用した、DC/DCコンバータの制御開発の一般的なステップを以下に示します。
- プラント(制御対象)モデル構築:DC/DCコンバータの回路モデルを作成
- 制御モデル構築:スイッチング素子に対するPWM信号の周波数やデューティ比を制御するモデルを作成
- システム評価:作成したプラントモデルと制御モデルを結合しシステムレベル評価
- ターゲット実装:制御モデルをマイコン/DSPやFPGAへ実装
それぞれのステップで最適なツールを選択し、開発の上流からシミュレーションを活用することで、開発効率や品質を向上させることが可能になります。
- Simscape Electronics™を使用しDC/DCコンバータの回路モデリングを素早く構築することが可能です。
- また作成したプラントモデルのパラメータ設定で、データシートを活用しますが、記載の無いパラメータについては、Optimization Toolbox™とSimulink Design Optimization™を使って計測データからパラメータ同定することが出来ます。
- 制御モデルは、Simulink®を使用しブロック線図形式で構築します。
- またフェールセーフによるモード制御の追加をする際は、Stateflow®を活用します。
- その他にも、外乱や負荷変動に対するフィードバック制御を構築する場合、一般的にPID制御を活用しますが、そのチューニングには、Control System Toolbox™とSimulink Control Design™を使い制御理論に基づいたパラメータの設定が可能です。
- マイコン/DSPやFPGAに実装する場合は、作成した制御モデルに、Fixed-Point Designer™を使用し固定小数点化してSimulink Coder™やEmbedded Coder®で自動Cコード生成、もしくはHDL Coder™ で自動HDLコード生成をします。
ユーザー事例
PWMの関連リソース
[コンバータ]
[モーター]
ソフトウェア リファレンス
[PWM]
参考: Simscape Power Systems, Simscape Electronics, Simulink Control Design, Embedded Coder, モーター制御, PWM(パルス幅変調)のビデオ, パワーエレクトロニクス シミュレーション, FOC(フィールドオリエンテッドコントロール), ブラシレスDC(BLDC)モーター制御, Clarke変換とPark変換, Raspberry Pi プログラミング, Arduino プログラミング