Understanding the Radar Equation | Understanding Radar Principles
From the series: Understanding Radar Principles
Brian Douglas, MathWorks
Learn how the radar equation combines several of the main parameters of a radar system in a way that gives you a general understanding of how the system will perform.
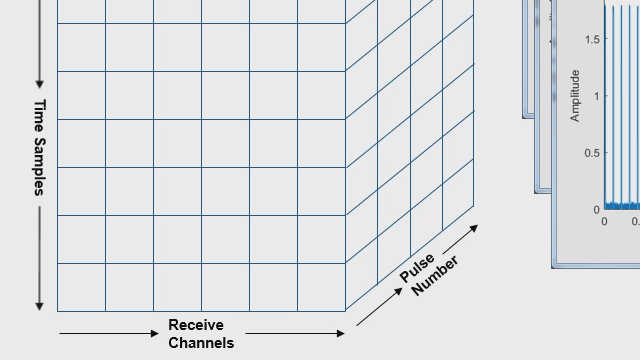
The radar equation is a function of transmit power, antenna gain, transmit frequency, radar cross-section of the object, and the propagation through the environment and radar components. Walk through each of these steps and watch a demonstration of how they contribute to the total received power of the reflected signal back at the radar.
Published: 13 Jun 2022