Archimedes optimization algorithm
Version 1.7 (17.9 KB) by
Prof. Dr. Essam H Houssein
Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems
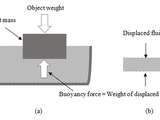
The difficulty and complexity of the real-world numerical optimization problems has grown manifold, which demands efficient optimization methods. To date, various metaheuristic approaches have been introduced, but only a few have earned recognition in research community. In this paper, a new metaheuristic algorithm called Archimedes optimization algorithm (AOA) is introduced to solve the optimization problems. AOA is devised with inspirations from an interesting law of physics Archimedes' Principle. It imitates the principle of buoyant force exerted upward on an object, partially or fully immersed in fluid, is proportional to weight of the displaced fluid. To evaluate performance, the proposed AOA algorithm is tested on CEC'17 test suite and four engineering design problems. The solutions obtained with AOA have outperformed well-known state-of-the-art and recently introduced metaheuristic algorithms such genetic algorithms (GA), particle swarm optimization (PSO), differential evolution variants L-SHADE and LSHADE-EpSin, whale optimization algorithm (WOA), sine-cosine algorithm (SCA), Harris' hawk optimization (HHO), and equilibrium optimizer (EO). The experimental results suggest that AOA is a high-performance optimization tool with respect to convergence speed and exploration-exploitation balance, as it is effectively applicable for solving complex problems. The source code is currently available for public from: https://www.mathworks.com/matlabcentral/fileexchange/79822-archimedes-optimization-algorithm
Cite As
Hashim, Fatma A., Kashif Hussain, Essam H. Houssein, Mai S. Mabrouk, and Walid Al-Atabany. "Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems." Applied Intelligence (2020): 1-21.
MATLAB Release Compatibility
Created with
R2020a
Compatible with any release
Platform Compatibility
Windows macOS LinuxTags
Acknowledgements
Inspired by: Archimedes optimization algorithm
Inspired: Archimedes optimization algorithm
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.