Routh-Hurwitz stability criterion
Version 1.2.0.0 (1.33 KB) by
Farzad Sagharchi
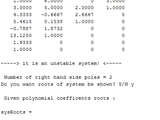
Hurwitz criterion basically tells us how many poles are located in the Left-Hand Plane, Right-Hand P
Routh-Hurwitz stability criterion identifies the conditions when the poles of a polynomial cross into the right
hand half plane and hence would be considered as unstable in control engineering.
Cite As
Farzad Sagharchi (2025). Routh-Hurwitz stability criterion (https://uk.mathworks.com/matlabcentral/fileexchange/17483-routh-hurwitz-stability-criterion), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2012a
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
Find more on Stability Analysis in Help Center and MATLAB Answers
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.