optimization-for-model-aircrafts
Model Aircraft Design Optimization
Copyright 2022 The MathWorks® Inc.
Introduction
This demo optimizes an aircraft with SAE Aero Design 2020 Regular Class problem statement as an example. A problem based approach is used to construct the design optimization problem. For SAE Aero Design 2020 Regular Class competition, each team's objective was to maximise their Final Flight Score (FFS) which was the sum of three highest Flight Scores (FS_i) and a Payload Prediction Bonus (PPB).
FFS = FS_1 + FS_2 + FS_3 + PPB
Each individual Flight Score (FS) was calculated as follows
FS = 120\times\frac{2\times N_s + W_{BP}}{b_w + l_{cargo}}
where,
N_s = No. of Spherical Payload
W_{BP} = Weight of Boxed Payload (lbs)
b_w = Wingspan (in)
l_{cargo} = Length of Payload Bay (in)
Therefore, this demo maximizes the following objective as it performs calculations in SI Units. Also, as only 1 spherical payload is considered.
Objective = 120\times \frac{2 + 2.2\times W_{BP}}{39.37\times(b_w + l_{cargo})}
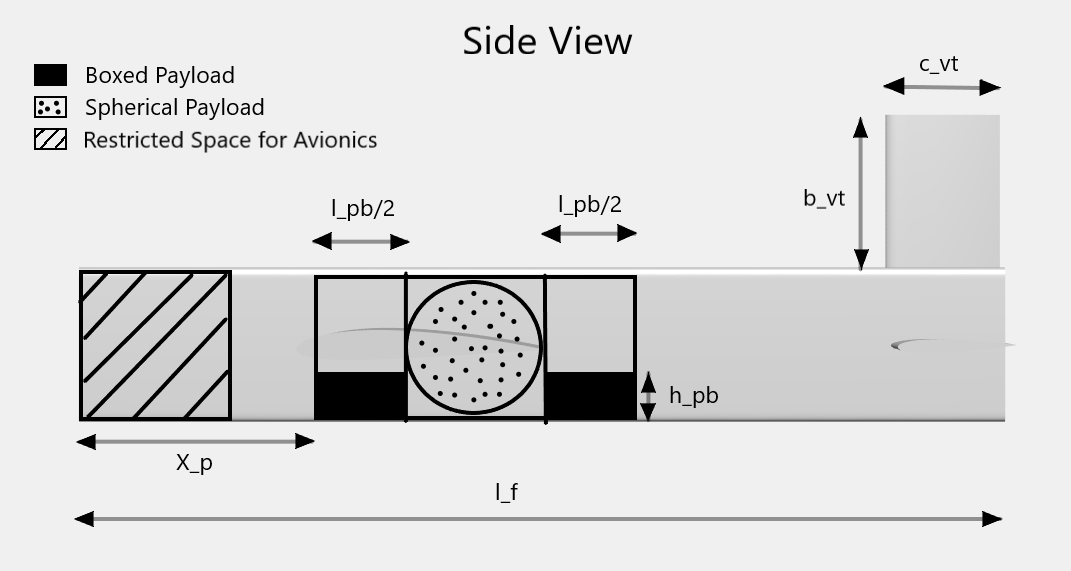
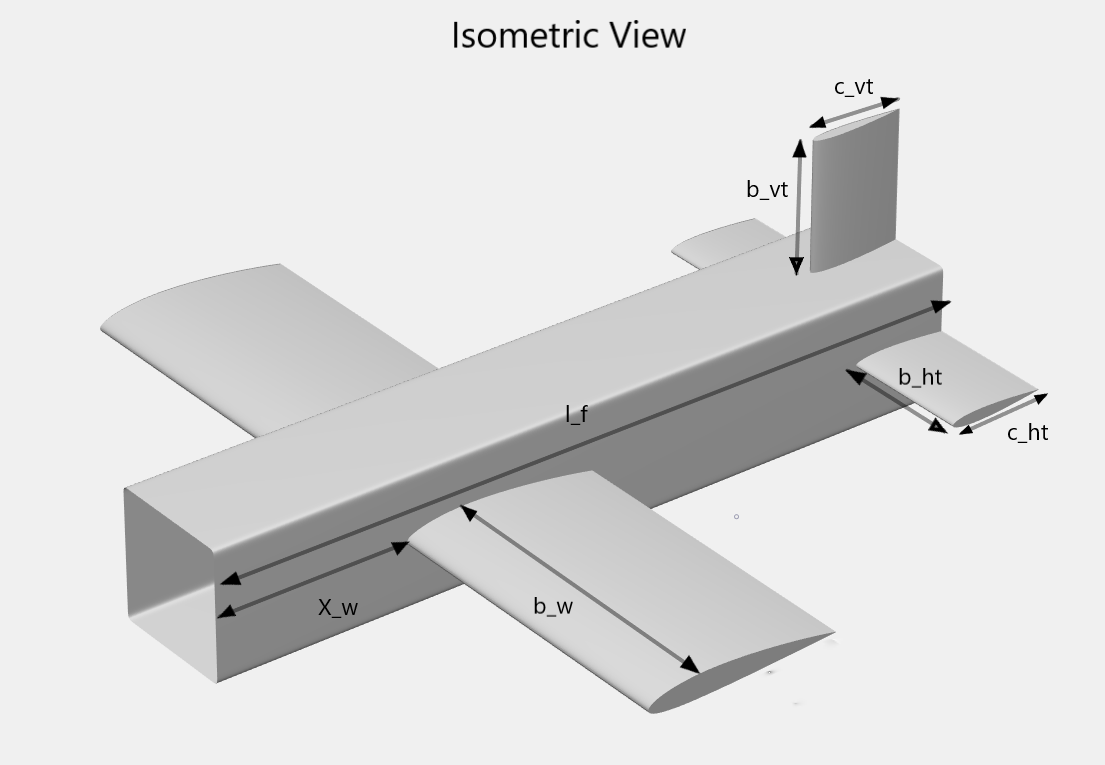
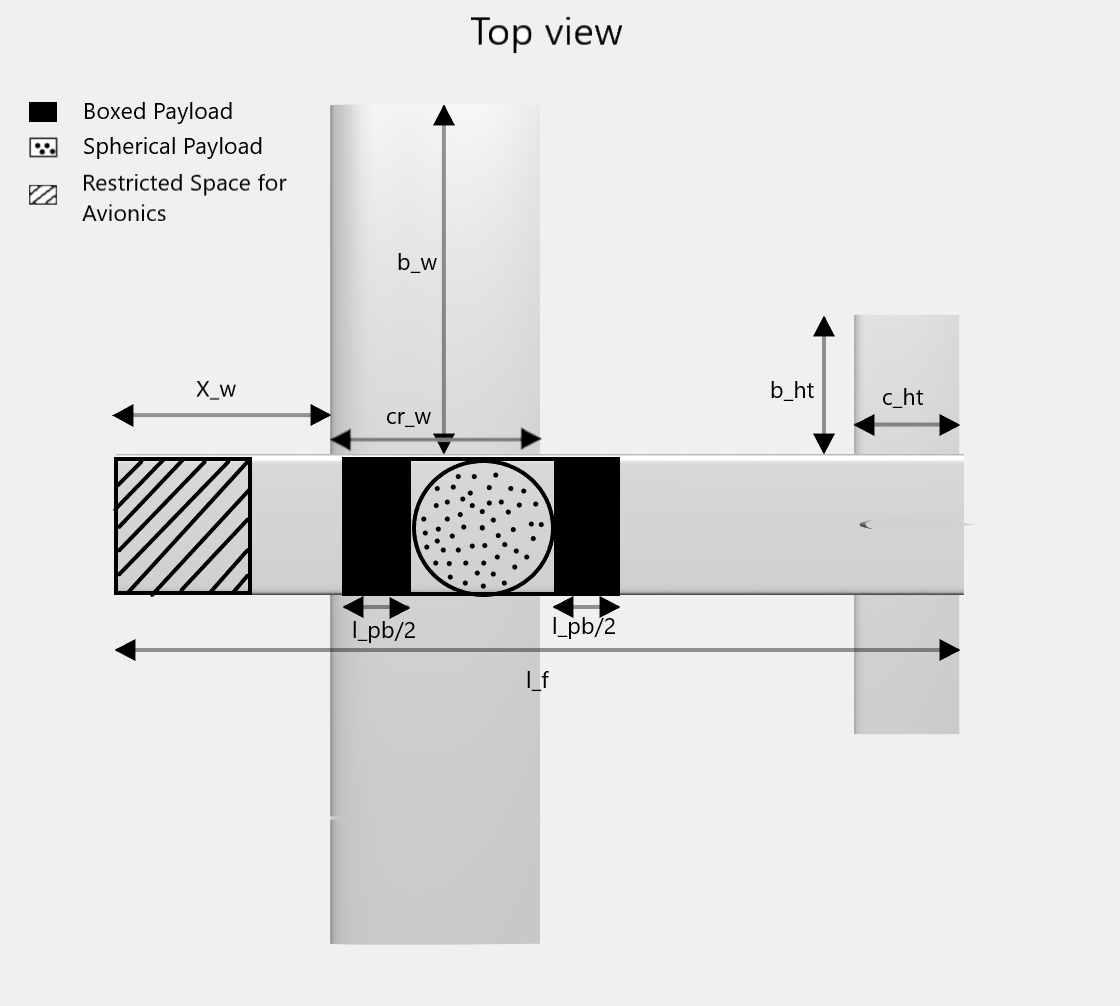
A problem based approach is used to construct the design optimization problem. All expressions evaluated during problem setup are stored as a hierarchy of structure inside the aircraft structure. Four domain specific functions incrementally construct the design problem by modelling domain specific expressions and adding any relevant constraints. Finally, a 12 dimensional optimization problem is obtained with the following optimization variables.
| Symbolic Variable | Physical Quantity |
|---|---|
b_w |
Wing Half Span |
cr_w |
Wing Root Chord |
lambda_w |
Wing Taper Ratio |
X_w |
Wing X Location |
b_{ht} |
Horizontal Tail Half Span |
c_{ht} |
Horizontal Tail Chord |
b_{vt} |
Vertical Tail Half Span |
c_{vt} |
Vertical Tail Chord |
l_f |
Length of Fuselage |
l_{pb} |
Length of Boxed Payload |
h_{pb} |
Height of Boxed Payload |
X_p |
Cargo Bay X Location |
Following is the representation of optimization variables.
 |
 |
 |
Code Structure
optimizeAircraft.mlx sets up and solves an aircraft design optimization problem. All other live functions model domain specific expressions and constraints and help incrementally setup the optimization problem.
Setup
- Clone the repository.
- Open MATLAB® and navigate to the repository.
- Open and execute the live script optimizeAircraft.mlx
MathWorks Products
Requires MATLAB release R2022a or newer
License
The license for Model Aircraft Design Optimization is available in the LICENSE.TXT file in this GitHub repository.
For any queries, contact the authors at roboticsarena@mathworks.com
Cite As
MathWorks Student Competitions Team (2025). optimization-for-model-aircrafts (https://github.com/mathworks/optimization-for-model-aircrafts/releases/tag/v1.0), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxTags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Aerodynamic Coefficients
Mass Moment of Inertia
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0 |



