Programmatically Build Simulink Models for CAN Communication

Algorithm Model

The example model AlgorithmModel.slx contains a subsystem block called "Algorithm". This block represents any given application algorithm developed in Simulink. A Gain (Simulink) block with value of 2 is inside this subsystem for demonstration purposes. This subsystem has a CAN signal input named "In1". This input value is scaled by the gain value. The scaled value is given as the output of this subsystem named "Out1". For experimentation, the gain value can be changed and the Gain block can be replaced by a different algorithm.

CAN Database File Access

You can access the contents of CAN DBC files with the canDatabase function. Through this function, details about network nodes, messages, and signals are available.

db = canDatabase("CANBus.dbc")

db = 
  Database with properties:

             Name: 'CANBus'
             Path: 'C:\Users\jpyle\Documents\MATLAB\Examples\vnt-ex60686316\CANBus.dbc'
            Nodes: {'ECU'}
         NodeInfo: [1×1 struct]
         Messages: {2×1 cell}
      MessageInfo: [2×1 struct]
       Attributes: {}
    AttributeInfo: [0×0 struct]
         UserData: []

A node "ECU" is defined in the example CAN DBC file as shown below.

node = nodeInfo(db,"ECU")

node = struct with fields:
             Name: 'ECU'
          Comment: ''
       Attributes: {}
    AttributeInfo: [0×0 struct]

The node receives a CAN message "AlgInput" containing a signal "InitialValue". The signal "InitialValue" is the input to the algorithm.

messageInfo(db,"AlgInput")

ans = struct with fields:
             Name: 'AlgInput'
     ProtocolMode: 'CAN'
          Comment: ''
               ID: 100
         Extended: 0
            J1939: []
           Length: 1
              DLC: 1
              BRS: 0
          Signals: {'InitialValue'}
       SignalInfo: [1×1 struct]
          TxNodes: {0×1 cell}
       Attributes: {}
    AttributeInfo: [0×0 struct]

The node transmits a CAN message "AlgOutput" containing a signal "ScaledValue". The signal "ScaledValue" is the output of the algorithm.

messageInfo(db,"AlgOutput")

ans = struct with fields:
             Name: 'AlgOutput'
     ProtocolMode: 'CAN'
          Comment: ''
               ID: 200
         Extended: 0
            J1939: []
           Length: 2
              DLC: 2
              BRS: 0
          Signals: {'ScaledValue'}
       SignalInfo: [1×1 struct]
          TxNodes: {'ECU'}
       Attributes: {}
    AttributeInfo: [0×0 struct]

Programmatically Build the Model

Open the Example Model

Open the example model to be configured.

open AlgorithmModel

Add and Configure CAN Configuration Block

Add and position a CAN Configuration block in the model.

add_block("canlib/CAN Configuration","AlgorithmModel/CAN Configuration")
set_param("AlgorithmModel/CAN Configuration","position",[50,330,250,410])

Set the "Device" parameter to have the model use the MathWorks® virtual CAN device.

set_param("AlgorithmModel/CAN Configuration","Device","MathWorks Virtual 1 (Channel 1)")

Add and Configure CAN Receive Block

Add and position a CAN Receive block in the model.

add_block("canlib/CAN Receive","AlgorithmModel/CAN Receive")
set_param("AlgorithmModel/CAN Receive","position",[50,200,250,280])

Add a Terminator (Simulink) block and position it. This is used to connect the function port of the CAN Receive block. In this example, simple message reception is performed. In general, placing a CAN Receive inside a Function-Call Subsystem (Simulink) is the preferred approach to modeling with CAN blocks.

add_block("simulink/Sinks/Terminator","AlgorithmModel/Terminator")
set_param("AlgorithmModel/Terminator","position",[310,210,330,230])

Set the "Device" parameter to have the model use the MathWorks virtual CAN device.

set_param("AlgorithmModel/CAN Receive","Device","MathWorks Virtual 1 (Channel 1)")

Add and Configure CAN Unpack Block

Add and position a CAN Unpack block in the model. By default, the block is in "Raw Data" mode.

add_block("canlib/CAN Unpack","AlgorithmModel/CAN Unpack")
set_param("AlgorithmModel/CAN Unpack","position",[350,220,600,300])

Set the following parameters in the CAN Unpack block in a single function call:

set_param("AlgorithmModel/CAN Unpack","DataFormat","CANdb specified signals","CANdbFile",db.Path,"MsgList","AlgInput")

If the "DataFormat" and "CANdbFile" parameters are already set on a block, the chosen message is changeable by only including the "MsgList" parameter.

Add and Configure CAN Pack Block

Add and position a CAN Pack block in the model.

add_block("canlib/CAN Pack","AlgorithmModel/CAN Pack")
set_param("AlgorithmModel/CAN Pack","position",[1000,220,1250,300])

Set the following parameters in the CAN Pack block in a single function call:

set_param("AlgorithmModel/CAN Pack","DataFormat","CANdb specified signals","CANdbFile",db.Path,"MsgList","AlgOutput")

Add and Configure CAN Transmit Block

Add and position a CAN Transmit block in the model.

add_block("canlib/CAN Transmit","AlgorithmModel/CAN Transmit")
set_param("AlgorithmModel/CAN Transmit","position",[1350,220,1550,300])

Set the "Device" parameter to have the model use the MathWorks virtual CAN device. Also, periodic transmission is enabled with the default timing.

set_param("AlgorithmModel/CAN Transmit","Device","MathWorks Virtual 1 (Channel 1)")
set_param("AlgorithmModel/CAN Transmit", "EnablePeriodicTransmit", "on")

Make Connections Between the Blocks

The CAN blocks and the algorithm block added in the model must now be connected. The port co-ordinates for all CAN blocks are required.

canRxPort = get_param("AlgorithmModel/CAN Receive","PortConnectivity");
canUnpackPort = get_param("AlgorithmModel/CAN Unpack","PortConnectivity");
subSystemPort = get_param("AlgorithmModel/Subsystem","PortConnectivity");
canPackPort = get_param("AlgorithmModel/CAN Pack","PortConnectivity");
canTxPort = get_param("AlgorithmModel/CAN Transmit","PortConnectivity");
terminatorPort = get_param("AlgorithmModel/Terminator","PortConnectivity");

[canRxPortFunc,canRxPortMsg] = canRxPort.Position;
[canUnpackPortIn,canUnpackPortOut] = canUnpackPort.Position;
[subSystemPortIn,subSystemPortOut] = subSystemPort.Position;
[canPackPortIn,canPackPortOut] = canPackPort.Position;
canTxPortMsg = canTxPort.Position;
terminatorPortIn = terminatorPort.Position;

Add lines to connect all of the blocks in the appropriate order.

add_line("AlgorithmModel",[canRxPortMsg ; canUnpackPortIn])
add_line("AlgorithmModel",[canUnpackPortOut ; subSystemPortIn])
add_line("AlgorithmModel",[subSystemPortOut ; canPackPortIn])
add_line("AlgorithmModel",[canPackPortOut ; canTxPortMsg])
add_line("AlgorithmModel",[canRxPortFunc ; terminatorPortIn])

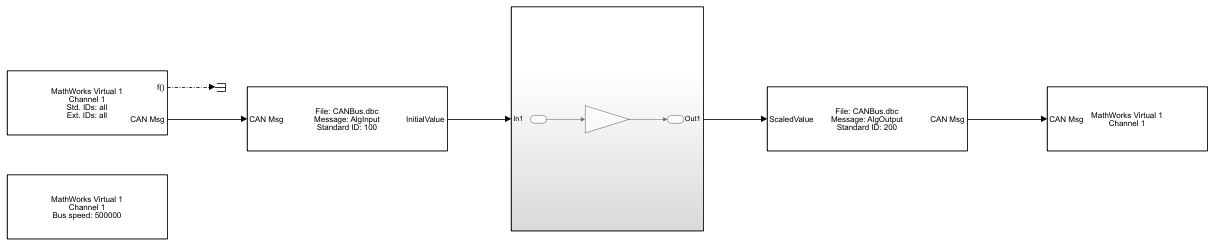
Completed Model

This is how the model looks after construction and configuration.

Test the Built Model

Configure a CAN Channel in MATLAB for Communication with the Algorithm Model

Create a CAN channel in MATLAB® using channel 2 of the MathWorks virtual CAN device. It will communicate with the CAN channel in the model. Also, attach the CAN database to the MATLAB channel to have it automatically decode incoming CAN data.

canCh = canChannel("MathWorks","Virtual 1",2);
canCh.Database = db;

For transmission from MATLAB to the model, use the CAN database to prepare a CAN message as input to the algorithm.

algInputMsg = canMessage(canCh.Database,"AlgInput");

Run the Algorithm Model

Assign the simulation time and start the simulation

set_param("AlgorithmModel","StopTime","inf")
set_param("AlgorithmModel","SimulationCommand","start")

Pause until the simulation is fully started.

while strcmp(get_param("AlgorithmModel","SimulationStatus"),"stopped")
end

Run the MATLAB Code

Start the MATLAB CAN channel.

start(canCh);

Transmit multiple CAN messages with different signal data as input to the model.

for value = 1:5
    algInputMsg.Signals.InitialValue = value*value;
    transmit(canCh,algInputMsg)
    pause(1)
end

Receive all messages from the bus. Note the instances of the "AlgInput" and "AlgOutput" messages, their timing, and signal values.

msg = receive(canCh,Inf,"OutputFormat","timetable")

msg=10×8 timetable
        Time        ID     Extended        Name            Data        Length      Signals       Error    Remote
    ____________    ___    ________    _____________    ___________    ______    ____________    _____    ______

    0.009728 sec    100     false      {'AlgInput' }    {[      1]}      1       {1×1 struct}    false    false 
    0.15737 sec     200     false      {'AlgOutput'}    {1×2 uint8}      2       {1×1 struct}    false    false 
    1.0121 sec      100     false      {'AlgInput' }    {[      4]}      1       {1×1 struct}    false    false 
    1.1574 sec      200     false      {'AlgOutput'}    {1×2 uint8}      2       {1×1 struct}    false    false 
    2.0146 sec      100     false      {'AlgInput' }    {[      9]}      1       {1×1 struct}    false    false 
    2.1574 sec      200     false      {'AlgOutput'}    {1×2 uint8}      2       {1×1 struct}    false    false 
    3.0177 sec      100     false      {'AlgInput' }    {[     16]}      1       {1×1 struct}    false    false 
    3.1574 sec      200     false      {'AlgOutput'}    {1×2 uint8}      2       {1×1 struct}    false    false 
    4.0219 sec      100     false      {'AlgInput' }    {[     25]}      1       {1×1 struct}    false    false 
    4.1574 sec      200     false      {'AlgOutput'}    {1×2 uint8}      2       {1×1 struct}    false    false 

The canSignalTimetable function provides an efficient way to separate and organize the signal values of CAN messages into individual timetables for each.

signalTimeTable = canSignalTimetable(msg)

signalTimeTable = struct with fields:
     AlgInput: [5×1 timetable]
    AlgOutput: [5×1 timetable]

signalTimeTable.AlgInput

ans=5×1 timetable
        Time        InitialValue
    ____________    ____________

    0.009728 sec          1     
    1.0121 sec            4     
    2.0146 sec            9     
    3.0177 sec           16     
    4.0219 sec           25     

signalTimeTable.AlgOutput

ans=5×1 timetable
       Time        ScaledValue
    ___________    ___________

    0.15737 sec         2     
    1.1574 sec          8     
    2.1574 sec         18     
    3.1574 sec         32     
    4.1574 sec         50     

Stop the CAN channel.

stop(canCh)

Stop the Algorithm Model

set_param("AlgorithmModel","SimulationCommand","stop")

Plot the Signal Data

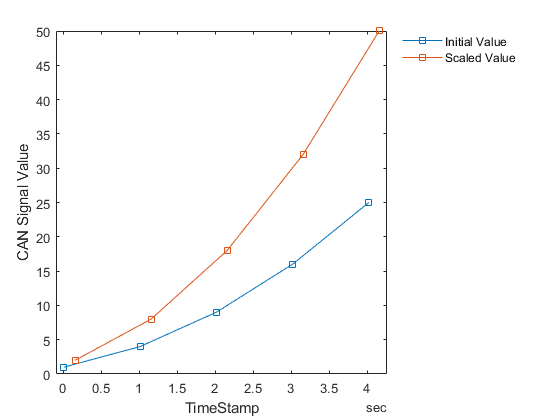
Plot the initial and scaled signal values of the CAN messages against the timestamps as they occurred on the virtual bus. Note the change in values as transmitted by MATLAB and the scaling of the data as performed by the model.

plot(signalTimeTable.AlgInput.Time,signalTimeTable.AlgInput.InitialValue,"Marker","square","MarkerIndices",1:5)
hold on
plot(signalTimeTable.AlgOutput.Time,signalTimeTable.AlgOutput.ScaledValue,"Marker","square","MarkerIndices",1:5)
hold off
xlabel("TimeStamp");
ylabel("CAN Signal Value");
legend("Initial Value","Scaled Value","Location","northeastoutside");
legend("boxoff");