2-D IFFT
Compute 2-D inverse fast Fourier transform (IFFT)
Libraries:
Computer Vision Toolbox /
Transforms
Description
The 2-D IFFT block computes the inverse discrete Fourier transform (IDFT) of a two-dimensional input matrix using the fast Fourier transform (FFT) algorithm. The equation for the 2-D IDFT f(x, y) of an M-by-N input matrix, F(m, n), is:
where and .
The block supports FFT implementation based on the FFTW library and an implementation based on a collection of Radix-2 algorithms. You can either manually select one of these implementations or let the block select one automatically.
Examples
Filter Image in Frequency Domain
Apply Gaussian lowpass filter to an image using the 2-D FFT block.
Ports
Input
Input data, specified as a vector or matrix of intensity values.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Output
Output data containing the 2-D IFFT of the input, returned as a vector or matrix. The size and data type of the output are the same as those of the input.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | fixed point
Complex Number Support: Yes
Parameters
Main
Specify the type of implementation to compute the FFT as one of these options:
FFTW— Select this option to use to support an arbitrary-length input signal. The block restricts generated code with theFFTWimplementation to host computers capable of running MATLAB®.Radix-2— Select this option to support bit-reversed processing, fixed and floating-point data, or portable C-code generation using Simulink Coder. The dimensions of the input matrix, M and N, must be powers of two. To work with other input sizes, use the Image Pad block to pad or truncate these dimensions to powers of two, or, if possible, choose theFFTWimplementation. For more information about the algorithms used by theRadix-2mode, see Radix-2 Implementation.Auto— Select this option to let the block choose the FFT implementation. For non-power-of-two transform lengths, the block restricts generated code to MATLAB host computers.
Specify whether the input to the block is in bit-reversed order or linear order. Select this parameter when you specify the input in bit-reversed order. Otherwise, clear this parameter. The block yields invalid output when you do not set this parameter correctly. For more information on the bit-reversed order of input, see Bit-Reversed Order.
Dependencies
To enable this parameter, set the FFT implementation
parameter to Auto or
Radix-2.
Select this parameter to specify that the block input is conjugate symmetric, and you want real-valued outputs. Otherwise, clear this parameter.
The 2-D FFT block yields conjugate symmetric output when you input real-valued data. Taking the 2-D IFFT of a conjugate symmetric input matrix produces real-valued output. Therefore, if the input to the 2-D IFFT block is conjugate symmetric, and you select this parameter, the block produces real-valued outputs. When you select this parameter, the block optimizes its computation method. You cannot select this parameter for fixed-point.
If you specify conjugate symmetric input data and do not select this parameter, the block outputs complex-valued data with small imaginary parts. The block outputs invalid data if you select this parameter with input data that is not conjugate symmetric input data.
Select this parameter to compute the scaled IFFT, which divides the output by the product of the dimension lengths of the FFT input dimension, as shown in this equation.
where and .
When you clear this parameter, the block computes the unscaled version of the IFFT, as shown in this equation.
Data Types
For details on the fixed-point block parameters, see Specify Fixed-Point Attributes for Blocks (DSP System Toolbox).
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in this block. For more information, see Lock the Output Data Type Setting (Fixed-Point Designer).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
Two numbers are bit-reversed values of each other when the binary representation of one
is the mirror image of the binary representation of the other. For example, in a three-bit
system, one and four are bit-reversed values of each other because the three-bit binary
representation of one, 001, is the mirror image of the three-bit binary
representation of four, 100. The diagram shows the row indices in linear
order. To put them in bit-reversed order:
Translate the indices into their binary representations with the minimum number of bits. In this example, the minimum number of bits is three because the binary representation of the largest row index, 7, is
111.Find the mirror image of each binary entry, and write it beside the original binary representation.
Translate each binary mirror image to its decimal representation.
The row indices now appear in bit-reversed order.

When you select the Output in bit-reversed order parameter of the 2-D FFT block, the block bit-reverses the order of both the rows and columns. All output values remain the same, but they appear in a different order.
These diagrams show the data types used in the 2-D FFT block for fixed-point signals. The block first casts inputs to the output data type and stores them in the output buffer. Each butterfly stage then processes signals in the accumulator data type, with the final butterfly casting its output back into the output data type. The block multiplies by a twiddle factor before each butterfly stage, in a decimation-in-time FFT, and after each butterfly stage in a decimation-in-frequency FFT.
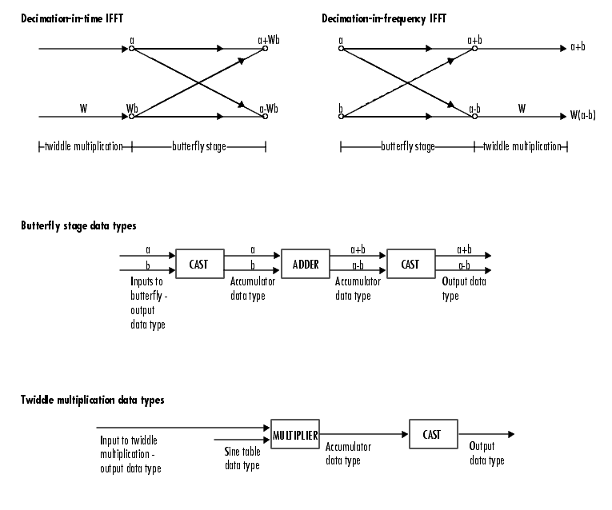
The multiplier output appears in the accumulator data type because both of the inputs to the multiplier are complex. For details on the complex multiplication performed, refer to Multiplication Data Types.
Algorithms
The FFTW implementation provides an optimized FFT calculation, including support for power-of-two and non-power-of-two transform lengths in both simulation and code generation. Generated code using the FFTW implementation can run only on computers capable of running MATLAB. The input must be of a floating-point data type.
The Radix-2 implementation supports bit-reversed processing, fixed or floating-point data, and enables the block to provide portable C-code generation using Simulink Coder. The dimensions of the input matrix, M and N, must be powers of two. To work with other input sizes, use the Image Pad block to pad or truncate these dimensions to powers of two.
The block implements one or more of these algorithms for Radix-2 implementation.
Butterfly operation
Double-signal algorithm
Half-length algorithm
Radix-2 decimation-in-time (DIT) algorithm
Radix-2 decimation-in-frequency (DIF) algorithm
| Parameter Settings | Algorithms Used for FFT Computation |
|---|---|
|
| Bit-reversed operation and radix-2 DIT |
|
| Radix-2 DIF |
|
| Bit-reversed operation and radix-2 DIT in conjunction with the half-length and double-signal algorithms |
|
| Radix-2 DIF in conjunction with the half-length and double-signal algorithms |
Note
The Input is conjugate symmetric parameter is not supported for fixed-point signals.
In certain situations, the Radix-2 algorithm computes all the possible trigonometric values of the twiddle factor:
where K is the greater value of either
M or N, and k is an integer in
the range [0, K – 1]. The block
stores these values in a table and retrieves them during simulation. This table summarizes
the number of table entries each for fixed-point and floating-point Radix-2 FFT
algorithms:
Number of Table Entries for N-Point FFT | |
|---|---|
Floating point | 3N/4 |
Fixed point | N |
References
[1] “FFTW Home Page.” Accessed February 23, 2022. https://www.fftw.org/.
[2] Frigo, M., and S.G. Johnson. “FFTW: An Adaptive Software Architecture for the FFT.” In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP ’98 (Cat. No.98CH36181), 3:1381–84. Seattle, WA, USA: IEEE, 1998. https://doi.org/10.1109/ICASSP.1998.681704.
Extended Capabilities
Usage notes and limitations:
When these conditions apply, the executable generated from this block relies on prebuilt dynamic library files (
.dllfiles) included with MATLAB:FFT implementation is set to
FFTW.Inherit FFT length from input dimensions is cleared, and the length of each dimension of the input matrix is a power of two.
Use the
packNGofunction to package the code generated from this block and all the relevant files in a compressed ZIP file. Using this ZIP file, you can relocate, unpack, and rebuild your project in another development environment where MATLAB is not installed.When the length of each dimension of the input matrix is a power of two, you can generate standalone C and C++ code from this block.
Version History
Introduced before R2006a
See Also
Blocks
- 2-D FFT | 2-D DCT | 2-D IDCT | 2-D FIR Filter
Functions
fft2|ifft2|bitrevorder(Signal Processing Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)