Matrix Rotations and Transformations
This example shows how to do rotations and transforms in 3-D using Symbolic Math Toolbox™ and matrices.
Define and Plot Parametric Surface
Define the parametric surface x(u,v), y(u,v), z(u,v) as follows.
syms u v x = cos(u)*sin(v); y = sin(u)*sin(v); z = cos(v)*sin(v);
Plot the surface using fsurf.
fsurf(x,y,z)
axis equal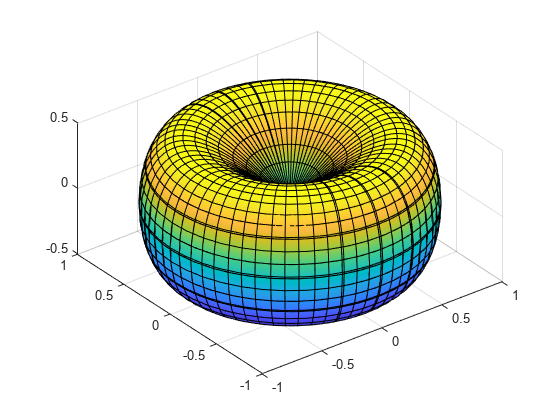
Create Rotation Matrices
Create 3-by-3 matrices Rx, Ry, and Rz representing plane rotations by an angle t about the x-, y-, and z-axis, respectively.
syms t
Rx = [1 0 0; 0 cos(t) -sin(t); 0 sin(t) cos(t)]Rx =
Ry = [cos(t) 0 sin(t); 0 1 0; -sin(t) 0 cos(t)]
Ry =
Rz = [cos(t) -sin(t) 0; sin(t) cos(t) 0; 0 0 1]
Rz =
Rotate About Each Axis in Three Dimensions
First, rotate the surface about the x-axis by 45 degrees counterclockwise.
xyzRx = Rx*[x;y;z]; Rx45 = subs(xyzRx, t, pi/4); fsurf(Rx45(1), Rx45(2), Rx45(3)) title('Rotating by \pi/4 about x, counterclockwise') axis equal

Rotate about the z-axis by 90 degrees clockwise.
xyzRz = Rz*Rx45; Rx45Rz90 = subs(xyzRz, t, -pi/2); fsurf(Rx45Rz90(1), Rx45Rz90(2), Rx45Rz90(3)) title('Rotating by \pi/2 about z, clockwise') axis equal

Rotate about the y-axis by 45 degrees clockwise.
xyzRy = Ry*Rx45Rz90; Rx45Rz90Ry45 = subs(xyzRy, t, -pi/4); fsurf(Rx45Rz90Ry45(1), Rx45Rz90Ry45(2), Rx45Rz90Ry45(3)) title('Rotating by \pi/4 about y, clockwise') axis equal
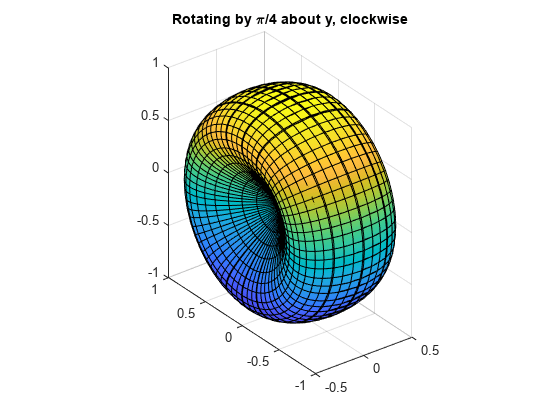
Scale and Rotate
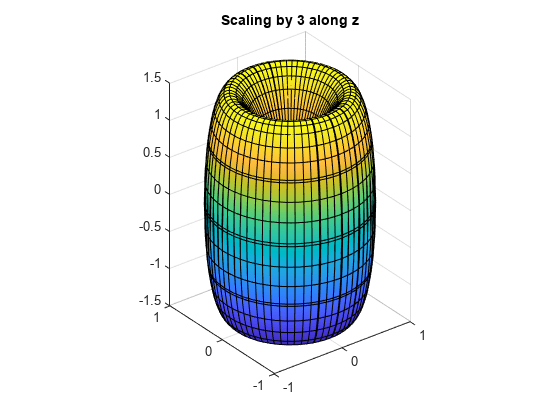
Scale the surface by the factor 3 along the z-axis. You can multiply the expression for z by 3, z = 3*z. The more general approach is to create a scaling matrix, and then multiply the scaling matrix by the vector of coordinates.
S = [1 0 0; 0 1 0; 0 0 3]; xyzScaled = S*[x; y; z]
xyzScaled =
fsurf(xyzScaled(1), xyzScaled(2), xyzScaled(3)) title('Scaling by 3 along z') axis equal
Rotate the scaled surface about the x-, y-, and z-axis by 45 degrees clockwise, in order z, then y, then x. The rotation matrix for this transformation is as follows.
R = Rx*Ry*Rz
R =
Use the rotation matrix to find the new coordinates.
xyzScaledRotated = R*xyzScaled; xyzSR45 = subs(xyzScaledRotated, t, -pi/4);
Plot the surface.
fsurf(xyzSR45(1), xyzSR45(2), xyzSR45(3)) title('Rotating by \pi/4 about x, y, and z, clockwise') axis equal

Check Properties of Rotation Matrix R
Rotation matrices are orthogonal matrices. Thus, the transpose of R is also its inverse, and the determinant of R is 1.
simplify(R.'*R)
ans =
simplify(det(R))
ans =