fit
Description
newExplainer = fit(explainer,queryPoints)queryPoints) and stores the computed Shapley values in the Shapley property
of newExplainer. The shapley object
explainer contains a machine learning model and the options for
computing Shapley values.
fit uses the Shapley value computation options that you specify
when you create explainer. You can change the options using the
name-value arguments of the fit function. The function returns a
shapley object newExplainer that contains the newly
computed Shapley values.
newExplainer = fit(explainer,queryPoints,Name=Value)UseParallel=true to compute Shapley values in parallel.
Examples
Train a regression model and create a shapley object. When you create a shapley object, if you do not specify query points, then the software does not compute Shapley values. Use the object function fit to compute the Shapley values for a specified query point. Then create a bar graph of the Shapley values by using the object function plot.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
load carbigCreate a table containing the predictor variables Acceleration, Cylinders, and so on, as well as the response variable MPG.
tbl = table(Acceleration,Cylinders,Displacement, ...
Horsepower,Model_Year,Weight,MPG);Removing missing values in a training set can help reduce memory consumption and speed up training for the fitrkernel function. Remove missing values in tbl.
tbl = rmmissing(tbl);
Train a blackbox model of MPG by using the fitrkernel function. Specify the Cylinders and Model_Year variables as categorical predictors. Standardize the remaining predictors.
rng("default") % For reproducibility mdl = fitrkernel(tbl,"MPG",CategoricalPredictors=[2 5], ... Standardize=true);
Create a shapley object. Specify the data set tbl, because mdl does not contain training data.
explainer = shapley(mdl,tbl)
explainer =
BlackboxModel: [1×1 RegressionKernel]
QueryPoints: []
BlackboxFitted: []
Shapley: []
X: [392×7 table]
CategoricalPredictors: [2 5]
Method: "interventional-kernel"
Intercept: 23.2474
NumSubsets: 64
explainer stores the training data tbl in the X property. By default, shapley subsamples 100 observations from the data in X, and stores their indices in the SampledObservationIndices property.
Compute the Shapley values of all predictor variables for the first observation in tbl. The fit object function uses the sampled observations instead of all of X to compute the Shapley values.
queryPoint = tbl(1,:)
queryPoint=1×7 table
Acceleration Cylinders Displacement Horsepower Model_Year Weight MPG
____________ _________ ____________ __________ __________ ______ ___
12 8 307 130 70 3504 18
explainer = fit(explainer,queryPoint);
For a regression model, fit computes Shapley values using the predicted response, and stores them in the Shapley property of the shapley object. Display the values in the Shapley property.
explainer.Shapley
ans=6×2 table
Predictor Value
______________ ________
"Acceleration" -0.33821
"Cylinders" -0.97631
"Displacement" -1.1425
"Horsepower" -0.62927
"Model_Year" -0.17268
"Weight" -0.87595
Plot the Shapley values for the query point by using the plot function.
plot(explainer)

The horizontal bar graph shows the Shapley values for all variables, sorted by their absolute values. Each Shapley value explains the deviation of the prediction for the query point from the average, due to the corresponding variable.
Train a classification model and create a shapley object. Then compute the Shapley values for two query points.
Load the CreditRating_Historical data set. The data set contains customer IDs and their financial ratios, industry labels, and credit ratings.
tbl = readtable("CreditRating_Historical.dat");Train a blackbox model of credit ratings by using the fitcecoc function. Use the variables from the second through seventh columns in tbl as the predictor variables.
blackbox = fitcecoc(tbl,"Rating", ... PredictorNames=tbl.Properties.VariableNames(2:7), ... CategoricalPredictors="Industry");
Create a shapley object with the blackbox model. Specify to sample 1000 observations from tbl to compute the Shapley values. Specify to use the extension to the Kernel SHAP algorithm.
rng("default") % For reproducibility explainer = shapley(blackbox,tbl,Method="conditional", ... NumObservationsToSample=1000);
Find two query points whose true rating values are AAA and BB, respectively.
sampleTbl = explainer.X(explainer.SampledObservationIndices,:); queryPoints(1,:) = sampleTbl(find(strcmp(sampleTbl.Rating,"AAA"),1),:); queryPoints(2,:) = sampleTbl(find(strcmp(sampleTbl.Rating,"BB"),1),:)
queryPoints=2×8 table
ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ _____ _____ _______ ________ _____ ________ _______
39364 0.61 0.694 0.122 5.409 0.359 3 {'AAA'}
44610 0.254 0.226 0.064 0.779 0.254 5 {'BB' }
Compute and plot the Shapley values for the first query point.
explainer1 = fit(explainer,queryPoints(1,:)); plot(explainer1)

Compute and plot the Shapley values for the second query point.
explainer2 = fit(explainer,queryPoints(2,:)); plot(explainer2)
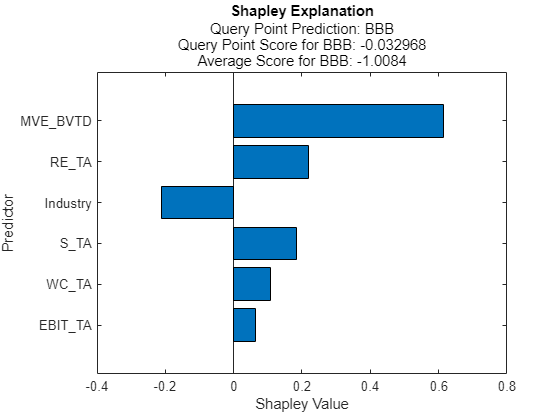
The true rating for the second query point is BB, but the predicted rating is BBB. The plot shows the Shapley values for the predicted rating.
explainer1 and explainer2 include the Shapley values for the first query point and second query point, respectively.
Train a regression model and create a shapley object. Use the object function fit to compute the Shapley values for the specified query points. Then plot the Shapley values for multiple query points by using the swarmchart object function.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
load carbigCreate a table containing the predictor variables Acceleration, Cylinders, and so on, as well as the response variable MPG.
tbl = table(Acceleration,Cylinders,Displacement, ...
Horsepower,Model_Year,Weight,MPG);Removing missing values in a training set helps to reduce memory consumption and speed up training for the fitrkernel function. Remove missing values in tbl.
tbl = rmmissing(tbl);
Train a blackbox model of MPG by using the fitrkernel function. Specify the Cylinders and Model_Year variables as categorical predictors. Standardize the remaining predictors.
rng("default") % For reproducibility mdl = fitrkernel(tbl,"MPG",CategoricalPredictors=[2 5], ... Standardize=true);
Create a shapley object. Because mdl does not contain training data, specify the data set tbl.
explainer = shapley(mdl,tbl)
explainer =
BlackboxModel: [1×1 RegressionKernel]
QueryPoints: []
BlackboxFitted: []
Shapley: []
X: [392×7 table]
CategoricalPredictors: [2 5]
Method: "interventional-kernel"
Intercept: 23.2474
NumSubsets: 64
explainer stores the training data tbl in the X property. By default, shapley subsamples 100 observations from the data in X, and stores their indices in the SampledObservationIndices property.
Compute the Shapley values for all observations in tbl. To speed up computations, the fit object function uses the sampled observations instead of all of X to compute the Shapley values. If you have a Parallel Computing Toolbox™ license, you can further reduce computational time by setting the UseParallel name-value argument.
explainer = fit(explainer,tbl,UseParallel=true);
For a regression model, fit computes Shapley values using the predicted response, and stores them in the Shapley property of the shapley object. Because explainer contains Shapley values for multiple query points, display the mean absolute Shapley values instead.
explainer.MeanAbsoluteShapley
ans=6×2 table
Predictor Value
______________ _______
"Acceleration" 0.5678
"Cylinders" 0.96799
"Displacement" 0.79668
"Horsepower" 0.78681
"Model_Year" 0.86258
"Weight" 0.987
For each predictor, the mean absolute Shapley value is the absolute value of the Shapley values, averaged across all query points. The Cylinders predictor has the greatest mean absolute Shapley value, and the Acceleration predictor has the smallest mean absolute Shapley value.
Visualize the Shapley values by using the swarmchart object function. Specify to use the "copper" colormap.
swarmchart(explainer,ColorMap="copper")
For each predictor, the function displays the Shapley values for the query points. The corresponding swarm chart shows the distribution of the Shapley values. The function determines the order of the predictors by using the mean absolute Shapley values.
Query points with low Weight values seem to have large positive Shapley values. That is, for these query points, the Weight predictor contributes to an increase in the MPG predicted value from the average. Similarly, query points with high Weight values seem to have large negative Shapley values. That is, for these query points, the Weight predictor contributes to a decrease in the MPG predicted value from the average. These results match the idea that car weights are inversely correlated with MPG values.
Input Arguments
Object explaining the blackbox model, specified as a shapley
object.
Query points at which fit explains predictions,
specified as a numeric matrix or a table. Each row of queryPoints
corresponds to one query point.
For a numeric matrix:
For a table:
If the predictor data
explainer.Xis a table, then all predictor variables inqueryPointsmust have the same variable names and data types as those inexplainer.X. However, the column order ofqueryPointsdoes not need to correspond to the column order ofexplainer.X.If the predictor data
explainer.Xis a numeric matrix, then the predictor names inexplainer.BlackboxModel.PredictorNamesand the corresponding predictor variable names inqueryPointsmust be the same. To specify predictor names during training, use thePredictorNamesname-value argument. All predictor variables inqueryPointsmust be numeric vectors.queryPointscan contain additional variables (response variables, observation weights, and so on), butfitignores them.fitdoes not support multicolumn variables or cell arrays other than cell arrays of character vectors.
If queryPoints contains NaNs for continuous
predictors and Method is "conditional", then the
Shapley values (Shapley) in
the returned object are NaNs. If you use a regression model that is a
Gaussian process regression (GPR), kernel, linear, neural network, or support vector
machine (SVM) model, then fit returns NaN
Shapley values for query points that contain missing predictor values or categories not
seen during training. For all other models, fit handles
missing values in the same way as explainer.BlackboxModel (that is,
the predict object function of
explainer.BlackboxModel or a function handle specified by
blackbox).
Before R2024a: You can specify only one query point using a row vector of numeric values or a single-row table.
Example: explainer.X(1,:) specifies the query point as the first
observation of the predictor data X in
explainer.
Data Types: single | double | table
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: fit(explainer,q,Method="conditional",UseParallel=true)
computes the Shapley values for the query point q using the extension to
the Kernel SHAP algorithm, and executes the computation in parallel.
Maximum number of predictor subsets to use for Shapley value computation, specified as a positive integer.
For details on how fit chooses the subsets to use,
see Computational Cost.
This argument is valid when the fit function uses the Kernel
SHAP algorithm or the extension to the Kernel SHAP algorithm. If you set the
MaxNumSubsets argument when Method is
"interventional", the software uses the Kernel SHAP algorithm.
For more information, see Algorithms.
Example: MaxNumSubsets=100
Data Types: single | double
Shapley value computation algorithm, specified as
"interventional" or "conditional".
"interventional"—fitcomputes the Shapley values with an interventional value function.fitoffers three interventional algorithms: Kernel SHAP [1], Linear SHAP [1], and Tree SHAP [2]. For each query point, the software selects an algorithm based on the machine learning modelexplainer.BlackboxModel"conditional"—fituses the extension to the Kernel SHAP algorithm [3] with a conditional value function.
The Method
property of newExplainer stores the name of the selected
algorithm. For more information, see Algorithms.
By default, the fit function uses the algorithm specified in
the Method
property of explainer.
Before R2023a: You can specify this argument as
"interventional-kernel" or
"conditional-kernel". fit supports
the Kernel SHAP algorithm and the extension of the Kernel SHAP algorithm.
Example: Method="conditional"
Data Types: char | string
Since R2024a
Function called after each query point evaluation, specified as a function handle. An output function can perform various tasks, such as stopping Shapley value computations, creating variables, or plotting results. For details and examples on how to write your own output functions, see Shapley Output Functions.
This argument is valid only when the fit function computes
Shapley values for multiple query points.
Data Types: function_handle
Flag to run in parallel, specified as a numeric or logical
1 (true) or 0
(false). If you specify UseParallel=true, the
fit function executes for-loop iterations by
using parfor. The loop runs in parallel when you
have Parallel Computing Toolbox™.
This argument is valid only when the fit function computes
Shapley values for multiple query points, or computes Shapley values for one query
point by using the Tree SHAP algorithm for an ensemble of trees, the Kernel SHAP
algorithm, or the extension to the Kernel SHAP algorithm.
Example: UseParallel=true
Data Types: logical
Output Arguments
More About
In game theory, the Shapley value of a player is the average marginal contribution of the player in a cooperative game. In the context of machine learning prediction, the Shapley value of a feature for a query point explains the contribution of the feature to a prediction (response for regression or score of each class for classification) at the specified query point.
The Shapley value of a feature for a query point is the contribution of the feature to the deviation from the average prediction. For a query point, the sum of the Shapley values for all features corresponds to the total deviation of the prediction from the average. That is, the sum of the average prediction and the Shapley values for all features corresponds to the prediction for the query point.
For more details, see Shapley Values for Machine Learning Model.
References
[1] Lundberg, Scott M., and S. Lee. "A Unified Approach to Interpreting Model Predictions." Advances in Neural Information Processing Systems 30 (2017): 4765–774.
[2] Lundberg, Scott M., G. Erion, H. Chen, et al. "From Local Explanations to Global Understanding with Explainable AI for Trees." Nature Machine Intelligence 2 (January 2020): 56–67.
[3] Aas, Kjersti, Martin Jullum, and Anders Løland. "Explaining Individual Predictions When Features Are Dependent: More Accurate Approximations to Shapley Values." Artificial Intelligence 298 (September 2021).
Extended Capabilities
To run in parallel, set the UseParallel name-value argument to
true in the call to this function.
For more general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2021aYou can run Shapley value computations in parallel when using the OutputFcn name-value argument by setting the UseParallel value
to true. To parallelize Shapley value computations, you must have
Parallel Computing Toolbox.
You can now compute Shapley values for multiple query points by using the queryPoints
argument. When working with multiple query points, you can use an output function to perform
various tasks, such as stopping Shapley value computations, creating variables, or plotting
results. To do so, specify the OutputFcn name-value argument.
When observations in the input predictor data (explainer.XqueryPoint)
contain missing values and the Method value is
"interventional", the fit function can use the
Tree SHAP algorithm for tree models and ensemble models of tree learners. In previous
releases, under these conditions, the fit function always used the
Kernel SHAP algorithm for tree-based models. For more information, including cases where the
software still uses Kernel SHAP instead of Tree SHAP for tree-based models, see Interventional Algorithms.
fit supports the Linear SHAP [1] algorithm for linear models and the Tree
SHAP [2] algorithm for tree models and ensemble
models of tree learners.
If you specify the Method name-value argument as
'interventional', the fit function selects an
algorithm based on the machine learning model type of explainer. The
Method property
of newExplainer stores the name of the selected algorithm.
The supported values of the Method name-value argument have changed
from 'interventional-kernel' and 'conditional-kernel'
to 'interventional' and 'conditional',
respectively.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)