predict
Predict responses using neighborhood component analysis (NCA) regression model
Syntax
Description
Examples
Load the sample data.
Download the housing data [1], from the UCI Machine Learning Repository [2]. The dataset has 506 observations. The first 13 columns contain the predictor values and the last column contains the response values. The goal is to predict the median value of owner-occupied homes in suburban Boston as a function of 13 predictors.
Load the data and define the response vector and the predictor matrix.
load('housing.data');
X = housing(:,1:13);
y = housing(:,end);Divide the data into training and test sets using the 4th predictor as the grouping variable for a stratified partitioning. This ensures that each partition includes similar amount of observations from each group.
rng(1) % For reproducibility cvp = cvpartition(X(:,4),'Holdout',56); Xtrain = X(cvp.training,:); ytrain = y(cvp.training,:); Xtest = X(cvp.test,:); ytest = y(cvp.test,:);
cvpartition randomly assigns 56 observations into a test set and the rest of the data into a training set.
Perform Feature Selection Using Default Settings
Perform feature selection using NCA model for regression. Standardize the predictor values.
nca = fsrnca(Xtrain,ytrain,'Standardize',1);Plot the feature weights.
figure()
plot(nca.FeatureWeights,'ro')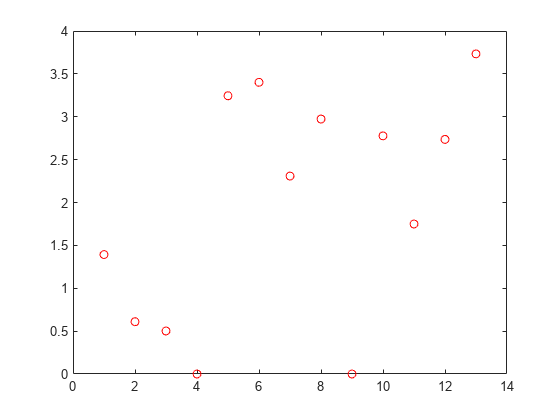
The weights of irrelevant features are expected to approach zero. fsrnca identifies two features as irrelevant.
Compute the regression loss.
L = loss(nca,Xtest,ytest,'LossFunction','mad')
L = 2.5394
Compute the predicted response values for the test set and plot them versus the actual response.
ypred = predict(nca,Xtest); figure() plot(ypred,ytest,'bo') xlabel('Predicted response') ylabel('Actual response')
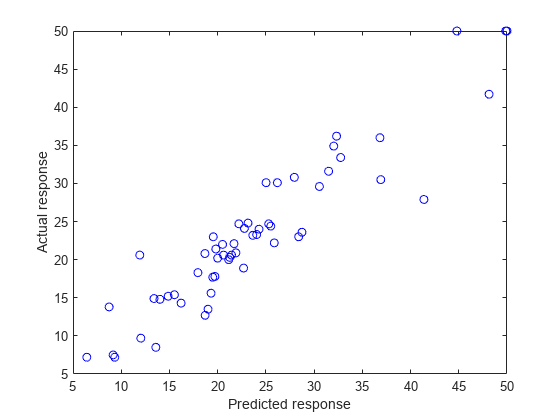
A perfect fit versus the actual values forms a 45 degree straight line. In this plot, the predicted and actual response values seem to be scattered around this line. Tuning (regularization parameter) value usually helps improve the performance.
Tune the regularization parameter using 10-fold cross-validation
Tuning means finding the value that will produce the minimum regression loss. Here are the steps for tuning using 10-fold cross-validation:
1. First partition the data into 10 folds. For each fold, cvpartition assigns 1/10th of the data as a training set, and 9/10th of the data as a test set.
n = length(ytrain);
cvp = cvpartition(Xtrain(:,4),'kfold',10);
numvalidsets = cvp.NumTestSets;Assign the values for the search. Create an array to store the loss values.
lambdavals = linspace(0,2,30)*std(ytrain)/n; lossvals = zeros(length(lambdavals),numvalidsets);
2. Train the neighborhood component analysis (nca) model for each value using the training set in each fold.
3. Fit a Gaussian process regression (gpr) model using the selected features. Next, compute the regression loss for the corresponding test set in the fold using the gpr model. Record the loss value.
4. Repeat this for each value and each fold.
for i = 1:length(lambdavals) for k = 1:numvalidsets X = Xtrain(cvp.training(k),:); y = ytrain(cvp.training(k),:); Xvalid = Xtrain(cvp.test(k),:); yvalid = ytrain(cvp.test(k),:); nca = fsrnca(X,y,'FitMethod','exact',... 'Lambda',lambdavals(i),... 'Standardize',1,'LossFunction','mad'); % Select features using the feature weights and a relative % threshold. tol = 1e-3; selidx = nca.FeatureWeights > tol*max(1,max(nca.FeatureWeights)); % Fit a non-ARD GPR model using selected features. gpr = fitrgp(X(:,selidx),y,'Standardize',1,... 'KernelFunction','squaredexponential','Verbose',0); lossvals(i,k) = loss(gpr,Xvalid(:,selidx),yvalid); end end
Compute the average loss obtained from the folds for each value. Plot the mean loss versus the values.
meanloss = mean(lossvals,2); figure; plot(lambdavals,meanloss,'ro-'); xlabel('Lambda'); ylabel('Loss (MSE)'); grid on;
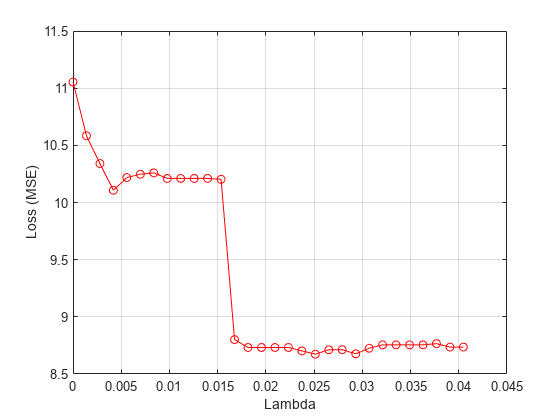
Find the value that produces the minimum loss value.
[~,idx] = min(meanloss); bestlambda = lambdavals(idx)
bestlambda = 0.0251
Perform feature selection for regression using the best value. Standardize the predictor values.
nca2 = fsrnca(Xtrain,ytrain,'Standardize',1,'Lambda',bestlambda,... 'LossFunction','mad');
Plot the feature weights.
figure()
plot(nca.FeatureWeights,'ro')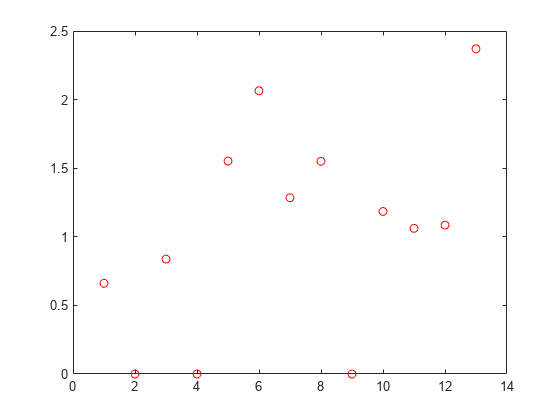
Compute the loss using the new nca model on the test data, which is not used to select the features.
L2 = loss(nca2,Xtest,ytest,'LossFunction','mad')
L2 = 2.0560
Tuning the regularization parameter helps identify the relevant features and reduces the loss.
Plot the predicted versus the actual response values in the test set.
ypred = predict(nca2,Xtest);
figure;
plot(ypred,ytest,'bo');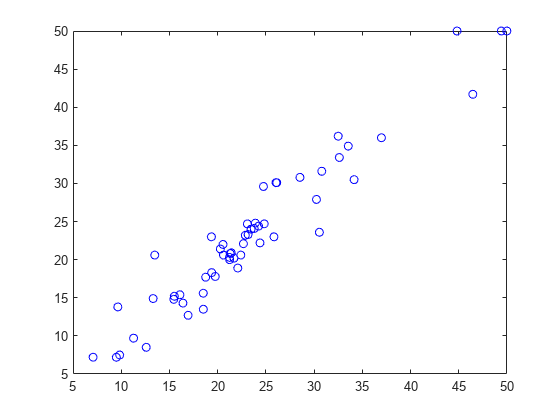
The predicted response values seem to be closer to the actual values as well.
References
[1] Harrison, D. and D.L., Rubinfeld. "Hedonic prices and the demand for clean air." J. Environ. Economics & Management. Vol.5, 1978, pp. 81-102.
[2] Lichman, M. UCI Machine Learning Repository, Irvine, CA: University of California, School of Information and Computer Science, 2013. https://archive.ics.uci.edu.
Input Arguments
Neighborhood component analysis model for regression, specified as a
FeatureSelectionNCARegression object.
Predictor variable values, specified as a table or an
n-by-p matrix, where
n is the number of observations and
p is the number of predictor variables used to train
mdl. By default, each row of X
corresponds to one observation, and each column corresponds to one
variable.
For a numeric matrix:
The variables in the columns of
Xmust have the same order as the predictor variables that trainedmdl.If you train
mdlusing a table (for example,Tbl), andTblcontains only numeric predictor variables, thenXcan be a numeric matrix. To treat numeric predictors inTblas categorical during training, identify categorical predictors by using theCategoricalPredictorsname-value argument offsrnca. IfTblcontains heterogeneous predictor variables (for example, numeric and categorical data types), andXis a numeric matrix, thenpredictthrows an error.
For a table:
Xmust contain all the predictors used to train the model.predictdoes not support multicolumn variables or cell arrays other than cell arrays of character vectors.If you train
mdlusing a table (for example,Tbl), then all predictor variables inXmust have the same variable names and data types as the variables that trainedmdl(stored inmdl.PredictorNames). However, the column order ofXdoes not need to correspond to the column order ofTbl. Also,TblandXcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.If you train
mdlusing a numeric matrix, then the predictor names inmdl.PredictorNamesmust be the same as the corresponding predictor variable names inX. To specify predictor names during training, use theCategoricalPredictorsname-value argument offsrnca. All predictor variables inXmust be numeric vectors.Xcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.
Data Types: table | single | double
Output Arguments
Predicted response values, returned as an n-by-1 vector, where n is the number of observations.
Version History
Introduced in R2016b
See Also
FeatureSelectionNCARegression | loss | fsrnca | refit | selectFeatures
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)