Watkins-Johnson Converter
This example shows the operation of a Watkins-Johnson Converter.
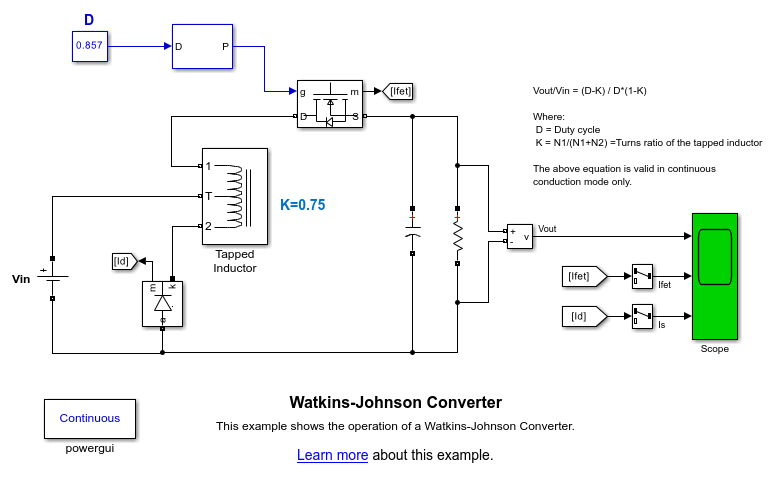
Description
The Watkins-Johnson (WJ) converter employs a tapped-inductor giving an extra-degree of freedom compared to the classical buck converter. The theoretical transfer function of the WJ converter is:
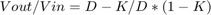
where 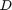 is the Duty cycle and
is the Duty cycle and 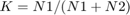 is the turns ratio of the tapped inductor.
is the turns ratio of the tapped inductor.
Note that the above equation is valid in continuous conduction mode only. For a giving conversion ratio, the WJ converter has the advantage of employing a larger duty cycle than the traditional classical buck converter. In our example, the tapped inductor is built using the SPS mutual inductance. By double-clicking on the Tapped Inductor block, you can specify the value in henrys and the turns ratio of the tapped inductor.
Simulation
Run the simulation and observe waveforms on Scope. The mean value of the load voltage (Vout) should be very close to the theoretical value of:
Vout = 24 * (0.857-0.75) /(0.855*(1-0.75) ) = 12.01 V