Universal Motor
Universal (or series) motor with electrical and torque characteristics
Libraries:
Simscape /
Electrical /
Electromechanical /
Brushed Motors
Description
The Universal Motor block represents the electrical and torque characteristics of a universal (or series) motor using the following equivalent circuit model.
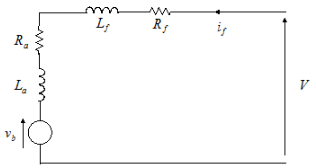
Where:
Ra is the armature resistance.
La is the armature inductance.
Rf is the field winding resistance.
Lf is the field winding inductance.
When you set the Model parameterization parameter to By
equivalent circuit parameters, you specify the equivalent circuit parameters for
this model. The Universal Motor block computes the motor torque as follows:
The magnetic field in the motor induces the following back emf vb in the armature:
where Laf is a constant of proportionality and ω is the angular velocity.
The mechanical power is equal to the power reacted by the back emf:
The motor torque is:
The torque-speed characteristic for the Universal Motor block
model is related to the parameters in the preceding figure. When you set the Model
parameterization parameter to By DC rated power, rated speed &
maximum torque or By DC rated power, rated speed & electrical
power, the block solves for the equivalent circuit parameters as follows:
For the steady-state torque-speed relationship when using a DC supply, L has no effect.
Sum the voltages around the loop:
Solve the preceding equation for if and substitute this value into the equation for torque:
The block uses the rated speed and power to calculate the rated torque. The block uses the rated torque and rated speed values in the preceding equation plus the corresponding electrical power to determine values for Rf+Ra and Laf.
When you set the Model parameterization parameter to By AC
rated power, rated speed, current & electrical power, then the block must
include the inductive terms La and
Lf in the model. This requires information about
the RMS rated current and voltage for the total inductance.
The block models motor inertia J and damping B for all values of the Model parameterization parameter. The output torque is:
The block produces a positive torque acting from the mechanical C to R ports.
Model Thermal Effects
You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block does not contain thermal ports.Show thermal port— The block contains multiple thermal conserving ports.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Examples
Ports
Conserving
Parameters
References
[1] Bolton, W. Mechatronics: Electronic Control Systems in Mechanical and Electrical Engineering, 3rd edition Pearson Education, 2004..
Extended Capabilities
Version History
Introduced in R2008a

