Coupled Lines (Three-Phase)
Magnetically couple three-phase lines
Libraries:
Simscape /
Electrical /
Passive /
Lines
Description
The Coupled Lines (Three-Phase) block models three magnetically coupled lines. Each line has a self-inductance, series resistance, and parallel conductance. In addition, there is a mutual inductance and mutual resistance between each pair of lines.
Use this block when the magnetic coupling in a three-phase network is nonnegligible. These effects are most prominent when:
The lines are parallel and close together.
The self-inductances of the lines are high.
The AC frequency of the network is high.
To model magnetic coupling of a single pair of lines, use the Coupled Lines (Pair) block. To model capacitive coupling between the lines, use the Transmission Line block.
Equivalent Circuit
The equivalent circuit shows the coupling between two arbitrary phases i, and j. The block models the magnetic coupling using such an equivalent circuit between each of the three phases a, b, and c.
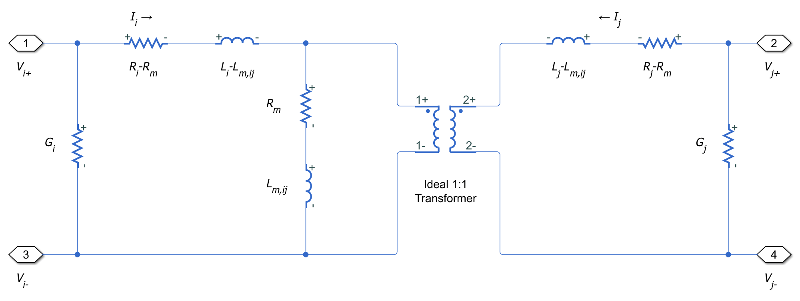
In this figure:
Ri and Rj are the series resistances of lines i and j, respectively.
Li and Lj are the self-inductances of lines i and j, respectively.
Rm,ij is the mutual resistance between lines i and j, respectively.
Lm,ij is the mutual inductance between lines i and j, respectively.
Gi and Gj are the leakage conductances of lines i and j, respectively.
Vi and Vj are voltage drops across lines i and j, respectively.
Ii and Ij are the currents through the resistors Ri-Rm,ij and Rj-Rm,ij, respectively.
Equations
The defining equation for this block is:
where:
Ia, Ib, and Ic are, in general, not equal to the currents in lines a, b, and c. These terminal currents make up the vector:
Inductive Coupling
To quantify the strength of the coupling between the two lines, you can use a coupling factor or coefficient of coupling k. The coupling factor relates the mutual inductance to the line self-inductances:
This coupling factor must fall in the range , where a negative coupling factor indicates a reversal in orientation of one of the coils. The magnitude of k indicates:
— There is no magnetic coupling between the two lines.
— The two lines are loosely coupled and mutual magnetic effects are small.
— The two lines are strongly coupled and mutual magnetic effects are large.
Mutual Resistance
If the three lines share a common return path, you can model the resistance of this return path using the Mutual resistance parameter Rm. This workflow is equivalent to setting the Mutual resistance to zero and explicitly modeling the return path resistance Rm, as shown in this diagram.
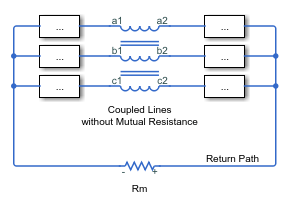
If the three lines do not share a common return path, set the mutual resistance parameter to zero and model each of the return resistances explicitly.
Faults
Since R2025a
To model a fault in the Coupled Lines (Three-Phase) block, in the Faults section, click Add fault next to the fault that you want to model. For more information about fault modeling, see Fault Behavior Modeling and Fault Triggering.
The Coupled Lines (Three-Phase) block allows you to model these types of fault:
Single-phase-to-ground fault (a-g, b-g, or c-g)
Two-phase fault (a-b, b-c, or c-a)
Two-phase-to-ground fault (a-b-g, b-c-g, or c-a-g)
Three-phase fault (a-b-c)
Three-phase-to-ground fault (a-b-c-g)
You can model a fault at one of the two three-phase connection ports or at both ports at the same time.
This figure shows how the block models the faults at the two three-phase ports:
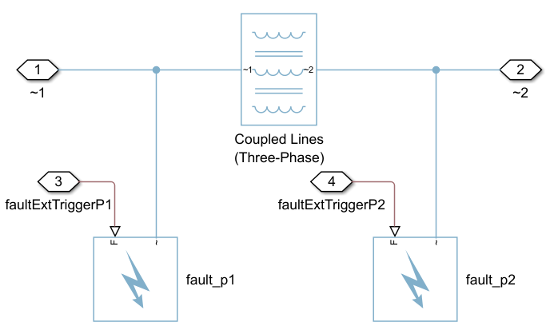
For more information about adding faults to blocks and specifying fault triggers, see Introduction to Simscape Faults.
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.