System Identification for PID Control
Plant Identification
In many situations, a dynamic representation of the system you want to control is not readily available. One solution to this problem is to obtain a dynamic model using identification techniques. The system is excited by a measurable signal and the corresponding response of the system is collected at some sample rate. The resulting input-output data is then used to obtain a model of the system such as a transfer function or a state-space model. This process is called system identification or estimation. The goal of system identification is to choose a model that yields the best possible fit between the measured system response to a particular input and the model’s response to the same input.
If you have a Simulink® model of your control system, you can simulate input/output data instead of measuring it. The process of estimation is the same. The system response to some known excitation is simulated, and a dynamic model is estimated based upon the resulting simulated input/output data.
Whether you use measured or simulated data for estimation, once a suitable plant model is identified, you impose control objectives on the plant based on your knowledge of the desired behavior of the system that the plant model represents. You then design a feedback controller to meet those objectives.
If you have System Identification Toolbox™ software, you can use PID Tuner for both plant identification and controller design in a single interface. You can import input/output data and use it to identify one or more plant models. Or, you can obtain simulated input/output data from a Simulink model and use that to identify one or more plant models. You can then design and verify PID controllers using these plants. PID Tuner also allows you to directly import plant models, such as one you have obtained from an independent identification task.
For an overview of system identification, see About System Identification (System Identification Toolbox).
Linear Approximation of Nonlinear Systems for PID Control
The dynamic behavior of many systems can be described adequately by a linear relationship between the system’s input and output. Even when behavior becomes nonlinear in some operating regimes, there are often regimes in which the system dynamics are linear. For example, the behavior of an operational amplifier or the lift-vs-force dynamics of aerodynamic bodies can be described by linear models, within a certain limited operating range of inputs. For such a system, you can perform an experiment (or a simulation) that excites the system only in its linear range of behavior and collect the input/output data. You can then use the data to estimate a linear plant model, and design a PID controller for the linear model.
In other cases, the effects of nonlinearities are small. In such a case, a linear model can provide a good approximation, such that the nonlinear deviations are treated as disturbances. Such approximations depend heavily on the input profile, the amplitude and frequency content of the excitation signal.
Linear models often describe the deviation of the response of a system from some equilibrium point, due to small perturbing inputs. Consider a nonlinear system whose output, y(t), follows a prescribed trajectory in response to a known input, u(t). The dynamics are described by dx(t)/dt = f(x, u), y = g(x,u) . Here, x is a vector of internal states of the system, and y is the vector of output variables. The functions f and g, which can be nonlinear, are the mathematical descriptions of the system and measurement dynamics. Suppose that when the system is at an equilibrium condition, a small perturbation to the input, Δu, leads to a small perturbation in the output, Δy:
For example, consider the system of the following Simulink block diagram:
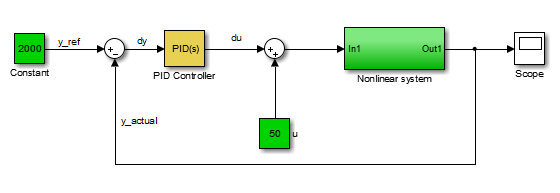
When operating in a disturbance-free environment, the nominal input of value 50 keeps the plant along its constant trajectory of value 2000. Any disturbances would cause the plant to deviate from this value. The PID Controller’s task is to add a small correction to the input signal that brings the system back to its nominal value in a reasonable amount of time. The PID Controller thus needs to work only on the linear deviation dynamics even though the actual plant itself might be nonlinear. Thus, you might be able to achieve effective control over a nonlinear system in some regimes by designing a PID controller for a linear approximation of the system at equilibrium conditions.
Linear Process Models
A common use case is designing PID controllers for the steady-state operation of manufacturing plants. In these plants, a model relating the effect of a measurable input variable on an output quantity is often required in the form of a SISO plant. The overall system may be MIMO in nature, but the experimentation or simulation is carried out in a way that makes it possible to measure the incremental effect of one input variable on a selected output. The data can be quite noisy, but since the expectation is to control only the dominant dynamics, a low-order plant model often suffices. Such a proxy is obtained by collecting or simulating input-output data and deriving a process model (low order transfer function with unknown delay) from it. The excitation signal for deriving the data can often be a simple bump in the value of the selected input variable.
Advanced System Identification Tasks
In PID Tuner, you can only identify single-input, single output, continuous-time plant models. Additionally, PID Tuner cannot perform the following system identification tasks:
Identify transfer functions of arbitrary number of poles and zeros. (PID Tuner can identify transfer functions up to three poles and one zero, plus an integrator and a time delay. PID Tuner can identify state-space models of arbitrary order.)
Estimate the disturbance component of a model, which can be useful for separating measured dynamics from noise dynamics.
Validate estimation by comparing the plant response against an independent dataset.
Perform residual analysis.
If you need these enhanced identification features, import your data into the System Identification app (System Identification (System Identification Toolbox)). Use the System Identification app to perform model identification and export the identified model to the MATLAB® workspace. Then import the identified model into PID Tuner for PID controller design.
For more information about the System Identification Tool, see Identify Linear Models Using System Identification App (System Identification Toolbox).
See Also
System Identification (System Identification Toolbox)