Sqrt
Calculate square root, signed square root, or reciprocal of square root
Libraries:
Simulink /
Math Operations
HDL Coder /
HDL Floating Point Operations
HDL Coder /
Math Operations
Alternative Configurations of Sqrt Block:
Signed Sqrt | Reciprocal Sqrt | Square Root | Signed Square Root | Reciprocal Square Root
Description
The Sqrt block calculates the square root, signed square root, or reciprocal of square root on the input signal. Select one of the following functions from the Function parameter list.
| Function | Description | Mathematical Expression | MATLAB® Equivalent |
|---|---|---|---|
sqrt
| Square root of the input |
|
sqrt
|
signedSqrt
| Square root of the absolute value of the input, multiplied by the sign of the input |
| — |
rSqrt
| Reciprocal of the square root of the input |
| — |
The block icon changes to match the function.
Examples
This example shows how to compute the square root of a negative-valued input signal as complex-valued output.
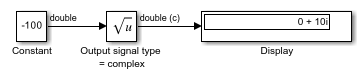
By setting the Function to sqrt and Output signal type to complex, the block produces the correct result of 0 + 10i for an input of -100. If you change the Output signal type to auto or real, the block outputs NaN.
This example shows how to compute the signed square root of a negative-valued input signal.
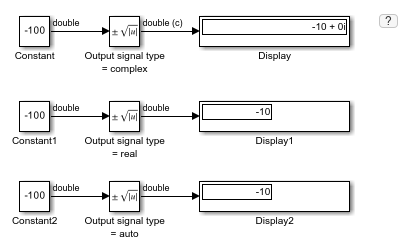
When the block input is negative and you set the Function to signedSqrt, the Sqrt block output is the same for any setting of the Output signal type parameter. By setting the Numerica display format of the first Display block to decimal (Stored Integer), you can see the value of the imaginary part for the complex output.
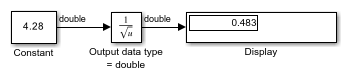
This example shows how to compute the rSqrt of a floating-point input signal. The Sqrt block has the following settings:
Method =
Newton-RaphsonNumber of iterations =
1Intermediate results data type =
Inherit: Inherit from input
After one iteration of the Newton-Raphson algorithm, the block output is within 0.0004 of the final value (0.4834).
This example shows how to compute the rSqrt of a fixed-point input signal. The Sqrt block has the following settings:
Method =
Newton-RaphsonNumber of iterations =
1Intermediate results data type =
Inherit: Inherit from input
After one iteration of the Newton-Raphson algorithm, the block output is within 0.0459 of the final value (0.4834).
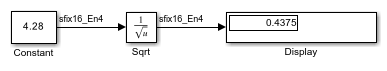
Ports
Input
Input signal to the block to calculate the square root, signed square root, or
reciprocal of square root. The sqrt function accepts
real or complex inputs, except for complex fixed-point signals.
signedSqrt and rSqrt do not
accept complex inputs. The input signal must be a floating point
number.
This table summarizes the support for complex types and negative
values for floating point, integer, and fixed-point data types for
sqrt, rSqrt, and
signedSqrt functions.
| Function | Data Type | Complex | Negative Values | |
|---|---|---|---|---|
| Input | Output | |||
sqrt | Floating point | Yes | Yes | Yes |
| Integer and fixed-point | No | No | No | |
| Floating point | No | No | Yes |
| Integer and fixed-point | No | No | No | |
signedSqrt | Floating point | No | Yes | Yes |
| Integer and fixed-point | No | No | No | |
If the input is negative, set the Output signal to complex for all
functions except signedSqrt.
Data Types: single | double | half | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Output
Output signal that is the square root, signed square root, or reciprocal of square root of the input signal. When the input is an integer or fixed-point type, the output must be floating point.
Data Types: single | double | half | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Parameters
Main
Specify the mathematical function that the block calculates. The block icon changes to match the function you select.
| Function | Block Icon |
|---|---|
sqrt
|
|
signedSqrt
|
|
rSqrt
|
|
The default value depends on the block configuration.
sqrtdefault — Sqrt and Square Root blockssignedSqrtdefault — Signed Sqrt and Signed Square Root blocksrSqrtdefault — Reciprocal Sqrt and Reciprocal Square Root blocks
Programmatic Use
Block Parameter:
Operator |
| Type: character vector |
Values:
'sqrt' | 'signedSqrt'
| 'rSqrt' |
Specify the output signal type of the block.
| Function | Input Signal Type | Output Signal Type | ||
|---|---|---|---|---|
| Auto | Real | Complex | ||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
Programmatic Use
Block Parameter:
OutputSignalType |
| Type: character vector |
Values:
'auto' | 'real' |
'complex' |
Default:
'auto' |
Specify the time interval between samples. To inherit the sample time, set this
parameter to -1. For more information, see Specify Sample Time.
Dependencies
This parameter is visible only if you set it to a value other than
-1. To learn more, see Blocks for Which Sample Time Is Not Recommended.
Programmatic Use
To set the block parameter value programmatically, use
the set_param function.
| Parameter: | SampleTime |
| Values: | "-1" (default) | scalar or vector in quotes |
Algorithm
Specify the method for computing the reciprocal of a square root.
| Method | Data Types Supported | When to Use This Method |
|---|---|---|
Exact
| Floating point | You do not want an approximation. The input or output must be floating point. |
Newton-Raphson
| Floating-point, fixed-point, and built-in integer types | You want a fast, approximate calculation. |
The Exact method provides results that are
consistent with MATLAB computations.
Dependencies
To enable this parameter, set Function to
rSqrt.
When Function is set to
sqrt or
signedSqrt, this parameter is set to
Exact.
Programmatic Use
Block Parameter:
AlgorithmType |
| Type: character vector |
Values:
'Exact' |
'Newton-Raphson' |
Default:
'Exact' |
Specify the number of iterations to perform the Newton-Raphson
algorithm. This parameter is valid with the rSqrt
function and the Newton-Raphson value for
Method.
If you enter 0, the block output is the initial
guess of the Newton-Raphson algorithm.
Programmatic Use
Block Parameter:
Iterations |
| Type: character vector |
| Values: integer |
Default:
'3' |
Data Types
The Data Type Assistant helps you set data
attributes. To use the Data Type Assistant, click ![]() . For more information, see Specify Data Types Using Data Type Assistant.
. For more information, see Specify Data Types Using Data Type Assistant.
Specify the data type for intermediate results when you set
Function to sqrt or
rSqrt.
The type can be inherited, specified directly, or expressed as a data
type object such as a Simulink.NumericType
object.
To avoid overflow, the intermediate data type must be larger than or equal to a data type that can contain the square of the output data type.
Follow these guidelines on setting an intermediate data type
explicitly for the square root function, sqrt:
| Input and Output Data Types | Intermediate Data Type |
|---|---|
| Input or output is double. | Use double. |
| Input or output is single, and any non-single data type is not double. | Use single or double. |
| Input and output are fixed point. | Use fixed point. |
Follow these guidelines on setting an intermediate data type
explicitly for the reciprocal square root function,
rSqrt:
| Input and Output Data Types | Intermediate Data Type |
|---|---|
| Input is double and output is not single. | Use double. |
| Input is not single and output is double. | Use double. |
| Input and output are fixed point. | Use fixed point. |
Caution
Do not set Intermediate results data type to
Inherit: Inherit from output
when:
You select
Newton-Raphsonto compute the reciprocal of a square root.The input data type is floating point.
The output data type is fixed point.
Under these conditions, selecting Inherit: Inherit
from output yields suboptimal performance and
produces an error.
To avoid this error, convert the input signal from a floating-point to fixed-point data type. For example, insert a Data Type Conversion block in front of the Sqrt block to perform the conversion.
Dependencies
To enable this parameter, set Function to
sqrt or
rSqrt.
Programmatic Use
Block Parameter:
IntermediateResultsDataTypeStr |
| Type: character vector |
Values: 'Inherit:
Inherit via internal rule' | 'Inherit:
Inherit from input' | 'Inherit: Inherit
from output' | 'double' |
'single', 'int8',
'uint8', int16,
'uint16', 'int32',
'uint32', 'int64',
'uint64',
fixdt(1,16,0),
fixdt(1,16,2^0,0). '<data
type expression>' |
Default: 'Inherit:
Inherit via internal rule' |
Specify the output data type. The type can be inherited, specified
directly, or expressed as a data type object such as a
Simulink.NumericType object.
Dependencies
When input is a floating-point data type smaller than single
precision, the Inherit: Inherit via internal
rule output data type depends on the setting of
the Inherit floating-point output type smaller than single precision configuration parameter. Data types are smaller than single
precision when the number of bits needed to encode the data type is
less than the 32 bits needed to encode the single-precision data
type. For example, half and
int16 are smaller than single
precision.
Programmatic Use
Block Parameter:
OutDataTypeStr |
| Type: character vector |
Values: 'Inherit:
Inherit via internal rule' | 'Inherit:
Inherit via back propagation' | 'Inherit:
Same as first input' | 'double'
| 'single' | 'half' |
'int8' | 'uint8' |
int16 | 'uint16' |
'int32' | 'uint32' |
'int64' | 'uint64' |
fixdt(1,16,0) |
fixdt(1,16,2^0,0) |
fixdt(1,16,2^0,0) | '<data
type expression>' |
Default: 'Inherit:
Same as first input' |
Specify the lower value of the output range that the software checks as a finite, real, double, scalar value.
If you specify a bus object as the data type for this block, do not
set the minimum value for bus data on the block. The software ignores
this setting. Instead, set the minimum values for bus elements of the
bus object specified as the data type. For more information, see Simulink.BusElement.
The software uses the minimum to perform:
Parameter range checking (see Specify Minimum and Maximum Values for Block Parameters) for some blocks.
Simulation range checking (see Specify Signal Ranges and Enable Simulation Range Checking).
Automatic scaling of fixed-point data types.
Optimization of the code that you generate from the model. This optimization can remove algorithmic code and affect the results of some simulation modes such as SIL or external mode. For more information, see Optimize using the specified minimum and maximum values (Embedded Coder).
Tips
Output minimum does not saturate or clip the actual output signal. Use the Saturation block instead.
Programmatic Use
Block Parameter:
OutMin |
| Type: character vector |
| Values: scalar |
Default:
'[]' |
Specify the upper value of the output range that the software checks as a finite, real, double, scalar value.
If you specify a bus object as the data type for this block, do not
set the maximum value for bus data on the block. The software ignores
this setting. Instead, set the maximum values for bus elements of the
bus object specified as the data type. For more information, see Simulink.BusElement.
The software uses the maximum value to perform:
Parameter range checking (see Specify Minimum and Maximum Values for Block Parameters) for some blocks.
Simulation range checking (see Specify Signal Ranges and Enable Simulation Range Checking).
Automatic scaling of fixed-point data types.
Optimization of the code that you generate from the model. This optimization can remove algorithmic code and affect the results of some simulation modes such as SIL or external mode. For more information, see Optimize using the specified minimum and maximum values (Embedded Coder).
Tips
Output maximum does not saturate or clip the actual output signal. Use the Saturation block instead.
Programmatic Use
Block Parameter:
OutMax |
| Type: character vector |
| Values: scalar |
Default:
'[]' |
Specify the rounding mode for fixed-point operations. For more information, see Rounding Modes (Fixed-Point Designer).
Programmatic Use
Block
Parameter:
RndMeth |
| Type: character vector |
Values:
'Ceiling' | 'Convergent' | 'Floor' |
'Nearest' | 'Round' | 'Simplest' |
'Zero' |
Default:
'Floor' |
Select to lock the output data type setting of this block against changes by the Fixed-Point Tool and the Fixed-Point Advisor. For more information, see Use Lock Output Data Type Setting (Fixed-Point Designer).
Programmatic Use
Block Parameter:
LockScale |
| Type: character vector |
Values:
'off' |
'on' |
Default:
'off' |
Specify whether overflows saturate or wrap.
on— Overflows saturate to either the minimum or maximum value that the data type can represent.off— Overflows wrap to the appropriate value that the data type can represent.
For example, the maximum value that the signed 8-bit integer int8
can represent is 127. Any block operation result greater than this maximum value causes
overflow of the 8-bit integer.
With this parameter selected, the block output saturates at 127. Similarly, the block output saturates at a minimum output value of -128.
With this parameter cleared, the software interprets the overflow-causing value as
int8, which can produce an unintended result. For example, a block result of 130 (binary 1000 0010) expressed asint8is -126.
Tips
Consider selecting this parameter when your model has a possible overflow and you want explicit saturation protection in the generated code.
Consider clearing this parameter when you want to optimize efficiency of your generated code. Clearing this parameter also helps you to avoid overspecifying how a block handles out-of-range signals. For more information, see Troubleshoot Signal Range Errors.
When you select this parameter, saturation applies to every internal operation on the block, not just the output or result.
In general, the code generation process can detect when overflow is not possible. In this case, the code generator does not produce saturation code.
Programmatic Use
To set the block parameter value programmatically, use
the set_param function.
| Parameter: | SaturateOnIntegerOverflow |
| Values: | 'on' (default) | 'off' |
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Alternative Configurations
The Signed Sqrt block sets Function
to signedSqrt.
Libraries:
Simulink /
Math Operations
The Reciprocal Sqrt block sets
Function to
rSqrt.
Libraries:
Simulink /
Math Operations
HDL Coder /
HDL Floating Point Operations
HDL Coder /
Math Operations
The Square Root block differs from the Sqrt block in name only.
Libraries:
Simulink /
Quick Insert /
Math Operations
The Signed Square Root block sets
Function to
signedSqrt.
The Signed Square Root block differs from the Signed Sqrt block in name only.
Libraries:
Simulink /
Quick Insert /
Math Operations
The Reciprocal Square Root block sets
Function to
rSqrt.
The Reciprocal Square Root block differs from the Reciprocal Sqrt block in name only.
Libraries:
Simulink /
Quick Insert /
Math Operations
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
| Function | Architecture | Description |
|---|---|---|
| SqrtFunction (default) | Compute the square root by using a pipelined shift-addition algorithm or
multiplication-based algorithm. The
Use the
UseMultiplier HDL block property in
combination with the LatencyStrategy
and CustomLatency properties to specify
whether to compute the square root by using a pipelined
shift and add or multiplication algorithm. Improve design
frequency and reduce resource utilization by setting the
UseMultiplier to
|
sqrt | SqrtNewton | Use the iterative Newton method to optimize area. |
sqrt | SqrtNewtonSingleRate | Use the single rate pipelined Newton method. Select this option to optimize speed, or if you want a single rate implementation. |
rSqrt | RecipSqrtNewton | Use the iterative Newton method to optimize area. To specify this architecture, set
Method to
|
rSqrt | RecipSqrtNewtonSingleRate | Use the single rate pipelined Newton method. Select this option to optimize speed, or if you want a single rate implementation. To specify this architecture,
set Method to
|
| General | |
|---|---|
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| Iterations | Number of iterations for
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| UseMultiplier | Select algorithm for Increase design frequency and
reduce resource utilization by setting the
UseMultiplier to
|
| LatencyStrategy | Specify whether to map the blocks in your design to Increase design frequency and reduce
resource utilization by setting the
UseMultiplier to
You can control
the pipeline stages for the iterative algorithm by setting
the LatencyStrategy to
|
| CustomLatency | When LatencyStrategy is set to
|
| IterationsPerPipeline | When you set LatencyStrategy to
For more information, see Sqrt (HDL Coder). |
| Native Floating Point | |
|---|---|
| HandleDenormals | Specify whether you want HDL Coder to insert additional logic to handle denormal numbers in your design.
Denormal numbers are numbers that have magnitudes less than the smallest floating-point
number that can be represented without leading zeros in the mantissa. The default is
|
The block supports these data types for HDL code generation:
| Input Port | Dimension | Fixed-Point | Floating-Point | Built-in Integers | Bus | Boolean | Complex Signal |
|---|---|---|---|---|---|---|---|
| Port_1 | Scalar Vector Matrix (up to 2-D) | Yes | Single Double | Yes | Yes | No | No |
This block has multi-cycle implementations that introduce additional latency in the generated code. To see the added latency, view the generated model or validation model. See Generated Model and Validation Model (HDL Coder).
Floating-Point Latency
| Architecture | Floating-Point Type | Latency Strategy | Latency (in cycles) | Custom Latency Support |
|---|---|---|---|---|
SqrtFunction | Single | Min | 16 | Yes |
| Max | 28 | |||
| Double | Min | 33 | ||
| Max | 58 |
Fixed-Point Latency
| Architecture | Maximum Latency (in cycles) | Description | Latency Strategy Support | Custom Latency Support |
|---|---|---|---|---|
SqrtFunction | To calculate the latency for fixed-point data types, see Algorithm in Sqrt (HDL Coder). | The maximum latency is determined by the output word length, and input and output fraction lengths, for fixed-point data. | Yes | Yes |
SqrtNewton | Iterations + 3 | The default value for Iterations HDL block property is 3. The recommended value for Iterations is from 2 through 10. If Iterations is outside the recommended range, HDL Coder generates a message. | No | No |
SqrtNewtonSingleRate | (Iterations* 4) + 6 | |||
RecipSqrtNewton | Number of iterations + 2 | The default value for Number of iterations block parameter is 3. The recommended value for Number of iterations is from 2 through 10. If Number of iterations is outside the recommended range, HDL Coder generates a message. | ||
RecipSqrtNewtonSingleRate | (Number of iterations* 4) + 5 |
These block parameter configurations are incompatible with HDL code generation.
| Block Parameter | Limitations and Considerations |
|---|---|
| Output Signal Type | Parameter value Complex is not
supported. |
| Method | When you set Function parameter to
rSqrt, use
Exact for floating-point data
types and Newton Raphson for
fixed-point data types. |
| Intermediate results data type | Parameter value other than Inherit: Inherit
via internal rule is not supported |
| Output | Choose an output port data type that is same as the input. |
| Integer rounding mode | Parameter value Convergent,
Round is not supported for
fixed-point types. |
You can use these HDL Coder optimizations to optimize the speed, area, and I/Os.
Area Optimization
| Optimization | Description |
|---|---|
| Resource Sharing (HDL Coder) | Resource sharing is an area optimization in which HDL Coder identifies multiple functionally equivalent resources and replaces them with a single resource. |
| Streaming (HDL Coder) | Streaming is an area optimization in which HDL Coder transforms a vector data path to a scalar data path (or to several smaller-sized vector data paths). |
Speed Optimization
| Optimization | Description |
|---|---|
| Distributed Pipelining (HDL Coder) | Distributed pipelining, or register retiming, is a speed optimization that moves existing delays in a design to reduce the critical path while preserving functional behavior. For the Sqrt block, HDL Coder distributes pipeline registers around the blocks instead of within them. |
| Clock-Rate Pipelining (HDL Coder) | Clock-rate pipelining is an optimization framework in HDL Coder that allows other speed and area optimizations to introduce latency at the clock rate. |
| Critical Path Estimation (HDL Coder) | To quickly identify the most likely critical path in your design, use Critical Path Estimation. Critical path estimation speeds up the iterative process of finding the critical path. To know blocks that are characterized in critical path estimation, see Characterized Blocks (HDL Coder). |
I/O Optimization
| Optimization | Description |
|---|---|
| Frame to Sample Conversion (HDL Coder) | To optimize the I/O needed for your design, use frame-to-sample conversion. This optimization converts frame-based vector or matrix inputs to smaller-sized samples or pixels for HDL code generation to target stream-based hardware and reduce the FPGA I/O needed to handle large input and output signals. |
HDL Coder implements reciprocal square-root operation in
ReciprocalRsqrtBasedNewton and
ReciprocalRsqrtBasedNewtonSingleRate architecture
by using Newton-Raphson iterative method, which is given by the equation:
Newton-Raphson-based implementation is incompatible with HDL code generation
in native floating-point mode. To generate HDL code in native floating-point
mode, select the SqrtFunction architecture in the HDL
Block properties.
Use SqrtFunction Architecture for Square Root Block (HDL Coder)
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
Version History
Introduced in R2010a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)