histogram
Plot histogram of multiparametric global sensitivity analysis results
Description
Examples
Load the target-mediated drug disposition (TMDD) model.
sbioloadproject tmdd_with_TO.sbprojGet the active configset and set the target occupancy (TO) as the response.
cs = getconfigset(m1);
cs.RuntimeOptions.StatesToLog = 'TO';Simulate the model and plot the TO profile.
sbioplot(sbiosimulate(m1,cs));
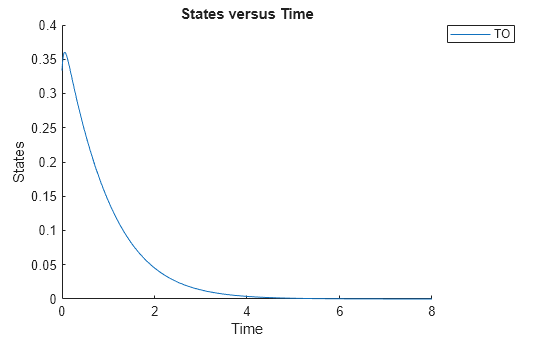
Define an exposure (area under the curve of the TO profile) threshold for the target occupancy.
classifier = 'trapz(time,TO) <= 0.1';Perform MPGSA to find sensitive parameters with respect to the TO. Vary the parameter values between predefined bounds to generate 10,000 parameter samples.
% Suppress an information warning that is issued during simulation. warnSettings = warning('off', 'SimBiology:sbservices:SB_DIMANALYSISNOTDONE_MATLABFCN_UCON'); rng(0,'twister'); % For reproducibility params = {'kel','ksyn','kdeg','km'}; bounds = [0.1, 1; 0.1, 1; 0.1, 1; 0.1, 1]; mpgsaResults = sbiompgsa(m1,params,classifier,Bounds=bounds,NumberSamples=10000)
mpgsaResults =
MPGSA with properties:
Classifiers: {'trapz(time,TO) <= 0.1'}
KolmogorovSmirnovStatistics: [4×1 table]
ECDFData: {4×4 cell}
SignificanceLevel: 0.0500
PValues: [4×1 table]
SupportHypothesis: [10000×1 table]
ParameterSamples: [10000×4 table]
Observables: {'TO'}
SimulationInfo: [1×1 struct]
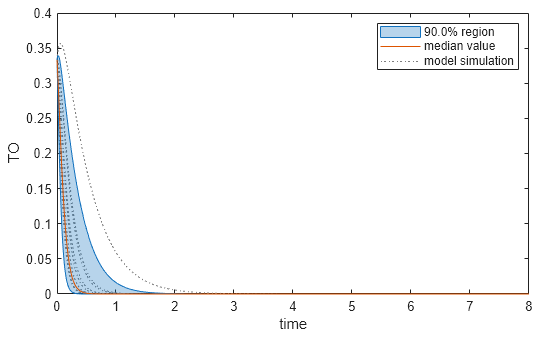
Plot the quantiles of the simulated model response.
plotData(mpgsaResults,ShowMedian=true,ShowMean=false);
Plot the empirical cumulative distribution functions (eCDFs) of the accepted and rejected samples. Except for km, none of the parameters shows a significant difference in the eCDFs for the accepted and rejected samples. The km plot shows a large Kolmogorov-Smirnov (K-S) distance between the eCDFs of the accepted and rejected samples. The K-S distance is the maximum absolute distance between two eCDFs curves.
h = plot(mpgsaResults);
% Resize the figure.
pos = h.Position(:);
h.Position(:) = [pos(1) pos(2) pos(3)*2 pos(4)*2];
To compute the K-S distance between the two eCDFs, SimBiology uses a two-sided test based on the null hypothesis that the two distributions of accepted and rejected samples are equal. See kstest2 (Statistics and Machine Learning Toolbox) for details. If the K-S distance is large, then the two distributions are different, meaning that the classification of the samples is sensitive to variations in the input parameter. On the other hand, if the K-S distance is small, then variations in the input parameter do not affect the classification of samples. The results suggest that the classification is insensitive to the input parameter. To assess the significance of the K-S statistic rejecting the null-hypothesis, you can examine the p-values.
bar(mpgsaResults)

The bar plot shows two bars for each parameter: one for the K-S distance (K-S statistic) and another for the corresponding p-value. You reject the null hypothesis if the p-value is less than the significance level. A cross (x) is shown for any p-value that is almost 0. You can see the exact p-value corresponding to each parameter.
[mpgsaResults.ParameterSamples.Properties.VariableNames',mpgsaResults.PValues]
ans=4×2 table
Var1 trapz(time,TO) <= 0.1
________ _____________________
{'kel' } 0.0021877
{'ksyn'} 1
{'kdeg'} 0.99983
{'km' } 0
The p-values of km and kel are less than the significance level (0.05), supporting the alternative hypothesis that the accepted and rejected samples come from different distributions. In other words, the classification of the samples is sensitive to km and kel but not to other parameters (kdeg and ksyn).
You can also plot the histograms of accepted and rejected samples. The historgrams let you see trends in the accepted and rejected samples. In this example, the histogram of km shows that there are more accepted samples for larger km values, while the kel histogram shows that there are fewer rejected samples as kel increases.
h2 = histogram(mpgsaResults);
% Resize the figure.
pos = h2.Position(:);
h2.Position(:) = [pos(1) pos(2) pos(3)*2 pos(4)*2];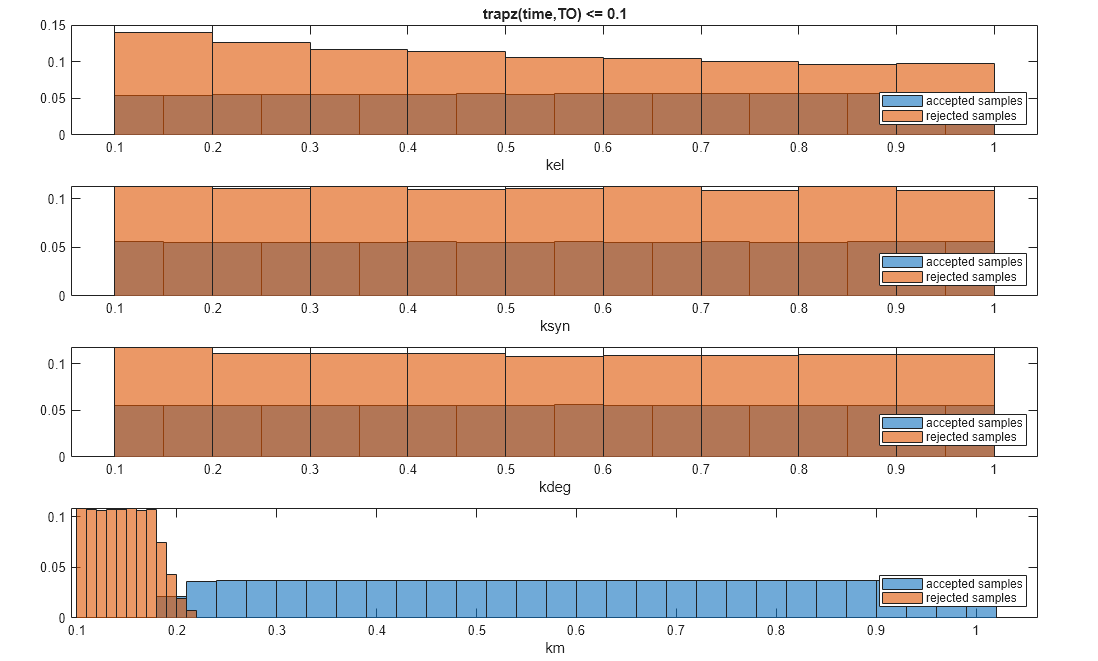
Restore the warning settings.
warning(warnSettings);
Input Arguments
Multiparametric global sensitivity analysis results, specified as a SimBiology.gsa.MPGSA object.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: h = histogram(results,'Classifier',1) specifies to plot
histograms of MPGSA results of the first classifier.
Input model quantities, namely parameters, species, or compartments, to plot, specified as a
character vector, string, string vector, cell array of character
vectors, or a vector of positive integers indexing into the
columns of the mpgsaObj.ParameterSamples
table.
Example: 'Parameters','k1'
Data Types: double | char | string | cell
Classifiers to plot, specified as a character vector, string, string vector, cell array of character vectors, or a vector of positive integers.
Specify the expressions of classifiers to plot as a character vector, string, string vector, cell array of character vectors. Alternatively, you can specify a vector of positive integers indexing into mpgsaObj.Classifiers.
Example: 'Classifiers',[1 3]
Data Types: double | char | string | cell
Color of accepted samples, specified as a three-element row vector, hexadecimal color
code, color name, or a short name. By default, the function uses the first MATLAB® default color. To view the default color order, enter
get(groot,'defaultAxesColorOrder') or see the ColorOrder property.
For details on valid color names and corresponding RGB triplets and hexadecimal codes, see Specify Plot Colors.
Example: 'AcceptedSamplesColor',[0.4,0.3,0.2]
Data Types: double
Color of rejected samples, specified as a three-element row vector, hexadecimal color
code, color name, or a short name. By default, the function uses the second MATLAB default color. To view the default color order, enter
get(groot,'defaultAxesColorOrder') or see the ColorOrder property.
For details on valid color names and corresponding RGB triplets and hexadecimal codes, see Specify Plot Colors.
Example: 'RejectedSamplesColor',[0.9,0.5,0.2]
Data Types: double
Output Arguments
Handle to the figure, specified as a figure handle.
References
[1] Tiemann, Christian A., Joep Vanlier, Maaike H. Oosterveer, Albert K. Groen, Peter A. J. Hilbers, and Natal A. W. van Riel. “Parameter Trajectory Analysis to Identify Treatment Effects of Pharmacological Interventions.” Edited by Scott Markel. PLoS Computational Biology 9, no. 8 (August 1, 2013): e1003166. https://doi.org/10.1371/journal.pcbi.1003166.
Version History
Introduced in R2020a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)