Envelope Extraction
This example shows how to extract the envelope of a signal.
Create a double sideband amplitude-modulated signal. The carrier frequency is 1 kHz. The modulation frequency is 50 Hz. The modulation depth is 100%. The sample rate is 10 kHz.
t = 0:1e-4:0.1; x = (1+cos(2*pi*50*t)).*cos(2*pi*1000*t); plot(t,x) xlim([0 0.04])

Extract the envelope using the hilbert function. The envelope is the magnitude of the analytic signal computed by hilbert. Plot the envelope along with the original signal. Store the name-value pair arguments of the plot function in a cell array for later use. The magnitude of the analytic signal captures the slowly varying features of the signal, while the phase contains the high-frequency information.
y = hilbert(x);
env = abs(y);
plot_param = {'Color', [0.6 0.1 0.2],'Linewidth',2};
plot(t,x)
hold on
plot(t,[-1;1]*env,plot_param{:})
hold off
xlim([0 0.04])
title('Hilbert Envelope')
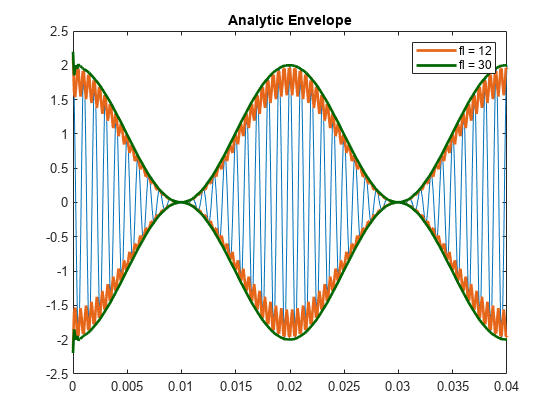
You can also use the envelope function to generate the signal envelope directly and modify the way it is computed. For example, you can adjust the length of the Hilbert filter used to find the analytic envelope. Using a filter length that is too small results in a distorted envelope.
fl1 = 12; [up1,lo1] = envelope(x,fl1,'analytic'); fl2 = 30; [up2,lo2] = envelope(x,fl2,'analytic'); param_small = {'Color',[0.9 0.4 0.1],'Linewidth',2}; param_large = {'Color',[0 0.4 0],'Linewidth',2}; plot(t,x) hold on p1 = plot(t,up1,param_small{:}); plot(t,lo1,param_small{:}); p2 = plot(t,up2,param_large{:}); plot(t,lo2,param_large{:}); hold off legend([p1 p2],'fl = 12','fl = 30') xlim([0 0.04]) title('Analytic Envelope')
You can generate moving RMS envelopes by using a sliding window. Using a window length that is too small results in a distorted envelope. Using a window length that is too large smooths out the envelope.
wl1 = 3; [up1,lo1] = envelope(x,wl1,'rms'); wl2 = 5; [up2,lo2] = envelope(x,wl2,'rms'); wl3 = 300; [up3,lo3] = envelope(x,wl3,'rms'); plot(t,x) hold on p1 = plot(t,up1,param_small{:}); plot(t,lo1,param_small{:}); p2 = plot(t,up2,plot_param{:}); plot(t,lo2,plot_param{:}); p3 = plot(t,up3,param_large{:}); plot(t,lo3,param_large{:}) hold off legend([p1 p2 p3],'wl = 3','wl = 5','wl = 300') xlim([0 0.04]) title('RMS Envelope')

You can generate peak envelopes by using spline interpolation over local maxima separated by an adjustable number of samples. Spreading out the samples too much smooths the envelope.
np1 = 5; [up1,lo1] = envelope(x,np1,'peak'); np2 = 50; [up2,lo2] = envelope(x,np2,'peak'); plot(t,x) hold on p1 = plot(t,up1,param_small{:}); plot(t,lo1,param_small{:}) p2 = plot(t,up2,param_large{:}); plot(t,lo2,param_large{:}) hold off legend([p1 p2],'np = 5','np = 50') xlim([0 0.04]) title('Peak Envelope')

Increasing the peak separation parameter can decrease the effect of spurious peaks due to noise. Introduce random noise to the signal. Use a 5-sample interval to see the effect of noise on the peak envelope. Repeat the exercise using a 25-sample interval.
rng default q = x + randn(size(x))/10; np1 = 5; [up1,lo1] = envelope(q,np1,'peak'); np2 = 25; [up2,lo2] = envelope(q,np2,'peak'); plot(t,q) hold on p1 = plot(t,up1,param_small{:}); plot(t,lo1,param_small{:}) p2 = plot(t,up2,param_large{:}); plot(t,lo2,param_large{:}) hold off legend([p1 p2],'np = 5','np = 25') xlim([0 0.04]) title('Peak Envelope')
