fir2
Frequency sampling-based FIR filter design
Description
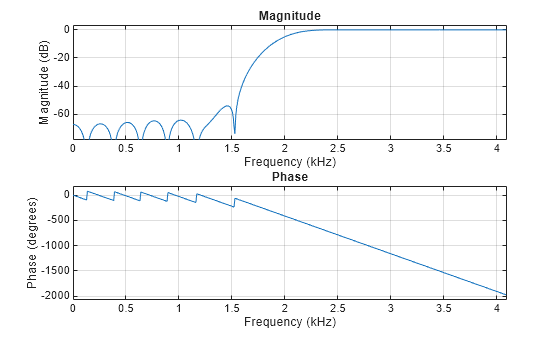
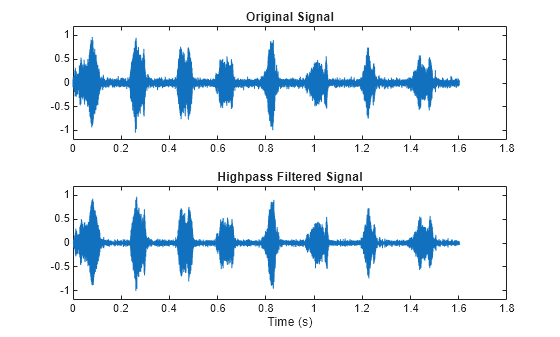
b = fir2(n,f,m)nth-order FIR filter with frequency-magnitude
characteristics specified in the vectors f and m.
The function linearly interpolates the desired frequency response
onto a dense grid and then uses the inverse Fourier transform and
a Hamming window to obtain the filter coefficients.
Examples
Input Arguments
Output Arguments
Algorithms
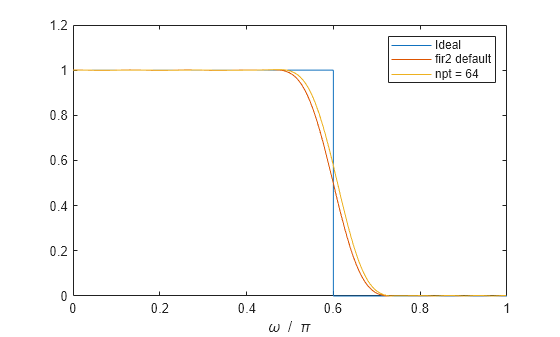
fir2 uses frequency sampling to design filters.
The function interpolates the desired frequency response linearly
onto a dense, evenly spaced grid of length npt. fir2 also
sets up regions of lap points around repeated
values of f to provide steep but smooth transitions.
To obtain the filter coefficients, the function applies an inverse
fast Fourier transform to the grid and multiplies by window.
References
[1] Jackson, L. B. Digital Filters and Signal Processing. 3rd Ed. Boston: Kluwer Academic Publishers, 1996.
[2] Mitra, Sanjit K. Digital Signal Processing: A Computer Based Approach. New York: McGraw-Hill, 1998.
Extended Capabilities
Version History
Introduced before R2006a