The Eye Measurement block extrapolates its 2-D histogram to a specified
symbol error rate whenever it generates bathtub curves or eye contours.
During extrapolation method, the block pre-processes the data, one symbol at a time on
only a 1-D slice of the said symbol. The block extrapolates the eye diagram at the specified
SER value using the interpolation between the adjacent bins.
The block provides five interpolation methods (none,
linear, spline,
pchip, and makima) and two
extrapolation methods (gaussian and
dualdirac) to extrapolate data.
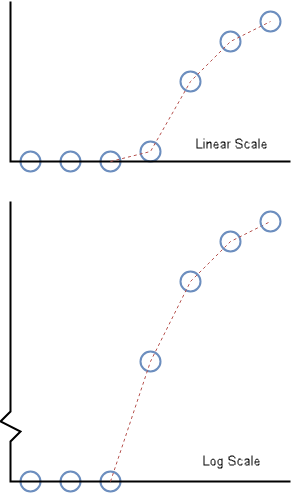
This image shows how the block uses interpolation methods to extrapolate data.
The blue dots represent the cumulative sum of the eye diagram going outward from the
center of the eye. The blue dot at the x-axis value zero represents the
eye opening. The dotted red line shows the interpolated samples.
The log scale image is used to create the bathtub curves. The discontinuity at the
logarithmic scale is to show the zero x-axis value. The linear scale
image shows how the cumulative sum of the 1-D slice of the eye looks on the same scale as
the slice itself..
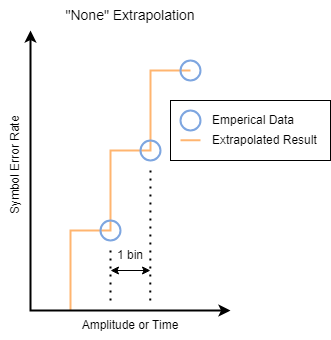
For example, the none extrapolation method uses a previous
neighbor interpolation of the cumulative sum an eye slice. For horizontal eye slices, the
extrapolation uses the timing origins. For vertical eye slices, the extrapolation uses the
symbol thresholds.
When moving outward from the center of the eye, it is a previous neighbor interpolation.
When moving across the eye from one side to the other, it appears as a next neighbor
interpolation that switches to a previous neighbor interpolation as you pass the center of
the eye. This way, the result for a symbol error rate is a conservative estimate from the
perspective of the eye opening, based on the data.
On the other hand, the dualdirac extrapolation algorithm
first fits the Dual-Dirac PDF to a column of the split histogram. Then it uses those
coefficients to calculate the inverse Dual-Dirac CDF for the specified SER(s). It is only
applicable to systems with an exponential impulse response whose time constant is on the
order of the time for one symbol, or less. The algorithm is also significantly slower that
the None extrapolation method.
This table summarizes the different extrapolation methods the block supports.
| Method | Description | Comments |
|---|
none | Uses previous neighbor interpolation of each eye slice to find the SER
values. The interpolated value at any query point is the value at the
previous sample grid point. |
|
dualdirac | Fits a Dual-Dirac model to each slice of the eye, then uses the fitted
model to find the SER values. |
Slower than other methods due to curve fitting. Less susceptible to noise, but less accurate to data.
|
gaussian | Uses the Gaussian defined by the sample mean and sample standard
deviation of each eye slice to find the SER values. |
Faster alternative to dualdirac. Best for automated optimization. Less susceptible to noise, but less accurate to data.
|
linear | Uses linear interpolation of each eye slice to find the SER
values. The interpolated value at any query point is based on linear
interpolation of the values at neighboring grid points in each respective
dimension. |
|
spline | Uses natural spline interpolation of the cumulative sum out from the
center of each eye slice to find SER values. |
Uses natural boundary conditions: the second derivative is zero at the end
points. Accurate to the data, but more susceptible to noise in individual
slices. Slowest of the interpolation methods, but faster than
dualdirac.
|
pchip | Uses shape-preserving piecewise cubic interpolation of each eye slice to
find the SER values. The interpolated value at any query point is
based on a shape-preserving piecewise cubic interpolation of the values at
neighboring grid points. |
Requires more computation time than
linear. Accurate to the data, but more susceptible to noise in individual
slices.
|
makima | Uses modified Akima cubic Hermite interpolation of each eye slice to find
the SER values. The interpolated value at a query point is based on
any piecewise function of polynomials with degree at most three. The Akima formula
is modified to avoid overshoots. |
Produces fewer undulations than spline, but
does not flatten as aggressively as pchip. Computation is more expensive than pchip, but
typically less than spline. Accurate to the data, but more susceptible to noise in individual
slices.
|