Automatic Data Segmentation and Feature Extraction for Reference Performance Test in Lab-Measured Battery Aging Data
Reference performance tests (RPT) are included in battery aging test design when there is no unified measurement available for obtaining remaining capacity or when additional measurements (slow rate cycles, pulses, EIS, etc.) are needed to characterize the battery's health. This example illustrates the use of a neural network for separating current pulses from regular charge-discharge steps and the extraction of features, that serve as health indicators, from the identified pulses.
Battery RPT data
The data used in this example is from one cell in ISU-ILCC Battery Aging Dataset [1], and is preprocessed to only contain raw measurements from RPTs (i.e., the cycling test data are excluded). The type of cell used in this dataset is NMC/graphite pouch cell with a rated capacity of 0.25Ah (1C = 0.25A). The RPT were performed using a 64-channel Neware BTS4000 series battery tester with cells placed in a temperature-controlled chamber set at 30°C. For this example, the essential measurements are:
RPT_Index - An integer identifying the RPT test number (starting from 1).
Steps - An integer identifying a step within the RPT profile (starting from 1).
Current (A) - The current measured in Amps.
Voltage (V) - The terminal voltage measured in Volts.
Capacity (Ah) - The cumulative charge/discharge capacity in a step measured in Amp-hour.
Relative Time (h:min:s.ms) - The time stamps relative to the start of each step.
Real Time (h:min:s.ms) - The time stamps with date and time.
Download the data from the MathWorks support files site and load it into MATLAB.
url = 'https://ssd.mathworks.com/supportfiles/predmaint/batteryagingdata/isuilcc/rpt/RPT_ISU_ILCC.zip'; downloadFolder = fullfile(tempdir,tempname); loc = websave('BatteryRPTDataset', url); unzip(loc, pwd) load("RPT_ISU.mat","data") head(data)
RPT_Index Record number status Jump Cycle Steps Current(A) Voltage(V) Capacity(Ah) Energy(Wh) Relative Time(h:min:s.ms) Real Time(h:min:s.ms)
_________ _____________ _________ ____ _____ _____ __________ __________ ____________ __________ _________________________ _______________________
1 1 "CC DChg" 1 1 1 -0.05 4.0119 0 0 00:00:00.000 2022-09-16 20:13:49.000
1 2 "CC DChg" 1 1 1 -0.05 4.0091 6.9437e-05 0.00027847 00:00:05.000 2022-09-16 20:13:54.000
1 3 "CC DChg" 1 1 1 -0.05 4.0073 0.00013888 0.00055682 00:00:10.000 2022-09-16 20:13:59.000
1 4 "CC DChg" 1 1 1 -0.05 4.006 0.00020833 0.00083505 00:00:15.000 2022-09-16 20:14:04.000
1 5 "CC DChg" 1 1 1 -0.05 4.0051 0.00027777 0.0011132 00:00:20.000 2022-09-16 20:14:09.000
1 6 "CC DChg" 1 1 1 -0.05 4.0042 0.00034721 0.0013913 00:00:25.000 2022-09-16 20:14:14.000
1 7 "CC DChg" 1 1 1 -0.05 4.0032 0.00041666 0.0016693 00:00:30.000 2022-09-16 20:14:19.000
1 8 "CC DChg" 1 1 1 -0.05 4.0026 0.0004861 0.0019473 00:00:35.000 2022-09-16 20:14:24.000
Visualize the data from one RPT
To better understand the RPT profile design in this dataset, visualize the current and voltage measurements from one RPT. At the beginning, the cells are discharged to 3V with C/5 current. Then, a sequence of a C/5 full-depth cycle, a C/2 full-depth cycle with pulses during discharge, and a C/2 full-depth cycle is performed. Plot the current, voltage, and time from the second RPT Test.
dataCycle = data(data.RPT_Index==2,:); currentCycle = dataCycle.("Current(A)"); voltageCycle = dataCycle.("Voltage(V)"); timeCycle = dataCycle.("Real Time(h:min:s.ms)"); relTimeCycle = seconds(timeCycle - timeCycle(1)); figure() yyaxis left plot(relTimeCycle,currentCycle,LineWidth=1.5) ylabel("Current (A)") yyaxis right plot(relTimeCycle,voltageCycle,LineWidth=1.5) ylabel("Voltage (V)") xlabel("Time (sec)")
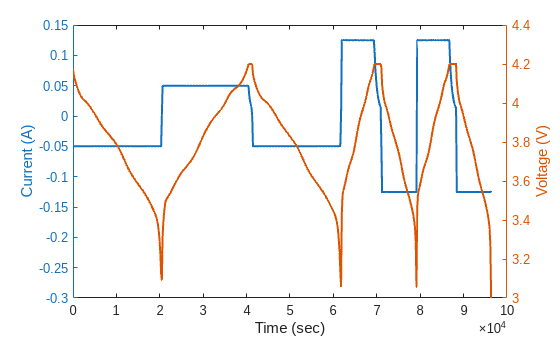
Zooming in to the first pulse in the RPT, it can be seen that when a discharge pulse is injected, the terminal voltage of the cell dips in response. Select 5 seconds before and after the pulse and plot the current and voltage for this duration.
dataPulse = dataCycle(ismember(dataCycle.Steps,[9,10,11]),:); timePulse = dataPulse.("Real Time(h:min:s.ms)"); timePulseDur = timePulse - timePulse(1); idx = timePulseDur<=duration(0,0,20)&timePulseDur>=duration(0,0,5); relTimePulse = seconds(timePulseDur(idx))-5; % Offset by 5 seconds currentPulse = dataPulse(idx,"Current(A)").("Current(A)"); voltagePulse = dataPulse(idx,"Voltage(V)").("Voltage(V)"); figure() yyaxis left plot(relTimePulse,currentPulse,LineWidth=1.5) ylabel("Current (A)") ylim([-0.3,0]) yyaxis right plot(relTimePulse,voltagePulse,LineWidth=1.5) ylabel("Voltage (V)") xlabel("Time (sec)") xlim([0,max(relTimePulse)]) ylim([4.12,4.2])
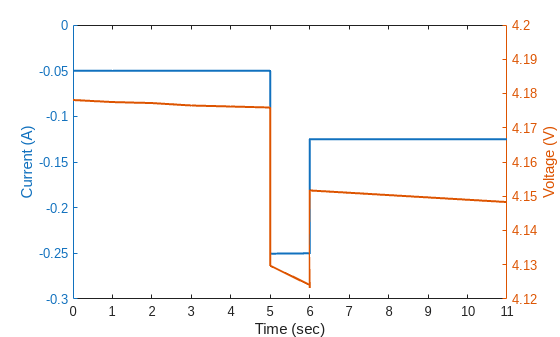
As the cell ages, the magnitude and pattern of this voltage dip could change, which provides useful information regarding the degradation. Thus, it is useful to extract features from these measurements and track changes in these features over cycles. However, as seen above, an RPT can contain both charge-discharge cycles and pulses. It is time consuming to manually extract the segments associated with the pulses. So, in the next section, a neural network is trained to identify pulses in an RPT measurement and the trained network is then used to identify all the pulses for feature extraction.
Train a neural network to perform automatic segmentation
A bi-directional long short-term memory (BiLSTM) model is trained to perform automatic segmentation. Assume that the data is partially labeled, and train the BiLSTM model on the available labeled data. Use the trained model to label the remaining unlabeled data.
Load predefined labels for a portion of the RPT data and append to the data table. Each point is labeled to be a part of a Pulse or Regular charge-discharge cycle. Points that are neither are not labeled and have an "undefined" label.
load("RPT_ISU_label.mat","label") data.Label = label; head(data)
RPT_Index Record number status Jump Cycle Steps Current(A) Voltage(V) Capacity(Ah) Energy(Wh) Relative Time(h:min:s.ms) Real Time(h:min:s.ms) Label
_________ _____________ _________ ____ _____ _____ __________ __________ ____________ __________ _________________________ _______________________ ___________
1 1 "CC DChg" 1 1 1 -0.05 4.0119 0 0 00:00:00.000 2022-09-16 20:13:49.000 <undefined>
1 2 "CC DChg" 1 1 1 -0.05 4.0091 6.9437e-05 0.00027847 00:00:05.000 2022-09-16 20:13:54.000 <undefined>
1 3 "CC DChg" 1 1 1 -0.05 4.0073 0.00013888 0.00055682 00:00:10.000 2022-09-16 20:13:59.000 <undefined>
1 4 "CC DChg" 1 1 1 -0.05 4.006 0.00020833 0.00083505 00:00:15.000 2022-09-16 20:14:04.000 <undefined>
1 5 "CC DChg" 1 1 1 -0.05 4.0051 0.00027777 0.0011132 00:00:20.000 2022-09-16 20:14:09.000 <undefined>
1 6 "CC DChg" 1 1 1 -0.05 4.0042 0.00034721 0.0013913 00:00:25.000 2022-09-16 20:14:14.000 <undefined>
1 7 "CC DChg" 1 1 1 -0.05 4.0032 0.00041666 0.0016693 00:00:30.000 2022-09-16 20:14:19.000 <undefined>
1 8 "CC DChg" 1 1 1 -0.05 4.0026 0.0004861 0.0019473 00:00:35.000 2022-09-16 20:14:24.000 <undefined>
To prepare the data for training, process the data using the helper function hProcessClassificationData into two cell variables, X and Y. The measured signal is returned as X and it is a cell array with 37 elements and each cell contains a two-row matrix. The first row is current, and the second row is voltage. The labels for each measured signal cell is returned as Y, which is also a 37 element cell array, with each cell being a categorical vector for the labels ("Regular" and "Pulse").
[X, Y] = hProcessClassficationData(data);
Visualize the preprocessed data for neural network training
currentPlot = X{2}(1,:);
voltagePlot = X{2}(2,:);
classes = categories(Y{2});
hPlotLabeledSignals(currentPlot, voltagePlot, classes, Y)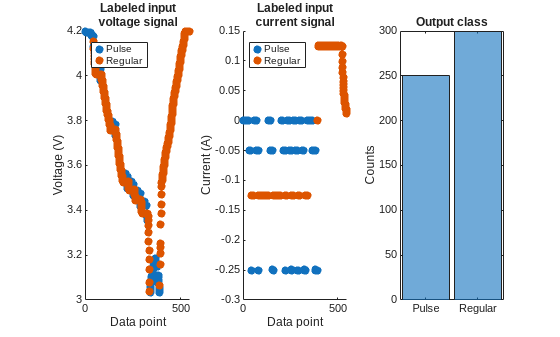
As seen in the above plots, voltage data by it self is not very different between the regular and pulse classes because the cell has to operate within its nominal range. However, the current data is clearly differentiated between the pulse and the regular classes. Thereby the combination of the current and voltage data as predictors can achieve good segmentation results. Further, the training data has been processed to balance the number of data points for regular and pulse classes to ensure a good fit.
Select 70% of RPTs for training using cvpartition function and use hTrainSegmentModel helper function to define and train the neural network.
rng default cv = cvpartition(max(data.RPT_Index),"HoldOut",0.3); idxTrain = training(cv); Xtrain = X(idxTrain,1); Ytrain = Y(idxTrain,1); net = hTrainSegmentModel(Xtrain,Ytrain);
Training on single CPU. |========================================================================================| | Epoch | Iteration | Time Elapsed | Mini-batch | Mini-batch | Base Learning | | | | (hh:mm:ss) | Accuracy | Loss | Rate | |========================================================================================| | 1 | 1 | 00:00:00 | 44.37% | 0.6741 | 0.0010 | | 50 | 50 | 00:00:18 | 87.23% | 0.3224 | 0.0010 | | 100 | 100 | 00:00:35 | 98.57% | 0.0443 | 0.0010 | |========================================================================================| Training finished: Max epochs completed.
Classify all steps using this trained model
The trained neural network can classify each data point. Given that one step can only associate to one class (i.e., a step is either "Regular" or "Pulse"), apply majority voting for each step to correct possible misclassifications at the beginning/end of the step. Use the helper function hRptDataParser to label each step as either "Regular" or "Pulse". The neural network model only classifies the step before the current pulse. So, the index for the step after pulses needs to be added explicitly after the model completes the segmentation.
segmentedData = hRptDataParser(data,net); head(segmentedData)
RPT_Index Record number status Jump Cycle Steps Current(A) Voltage(V) Capacity(Ah) Energy(Wh) Relative Time(h:min:s.ms) Real Time(h:min:s.ms) Label Individual_class Step_class
_________ _____________ _________ ____ _____ _____ __________ __________ ____________ __________ _________________________ _______________________ ___________ ________________ __________
1 1 "CC DChg" 1 1 1 -0.05 4.0119 0 0 00:00:00.000 2022-09-16 20:13:49.000 <undefined> Pulse Regular
1 2 "CC DChg" 1 1 1 -0.05 4.0091 6.9437e-05 0.00027847 00:00:05.000 2022-09-16 20:13:54.000 <undefined> Pulse Regular
1 3 "CC DChg" 1 1 1 -0.05 4.0073 0.00013888 0.00055682 00:00:10.000 2022-09-16 20:13:59.000 <undefined> Pulse Regular
1 4 "CC DChg" 1 1 1 -0.05 4.006 0.00020833 0.00083505 00:00:15.000 2022-09-16 20:14:04.000 <undefined> Pulse Regular
1 5 "CC DChg" 1 1 1 -0.05 4.0051 0.00027777 0.0011132 00:00:20.000 2022-09-16 20:14:09.000 <undefined> Pulse Regular
1 6 "CC DChg" 1 1 1 -0.05 4.0042 0.00034721 0.0013913 00:00:25.000 2022-09-16 20:14:14.000 <undefined> Pulse Regular
1 7 "CC DChg" 1 1 1 -0.05 4.0032 0.00041666 0.0016693 00:00:30.000 2022-09-16 20:14:19.000 <undefined> Pulse Regular
1 8 "CC DChg" 1 1 1 -0.05 4.0026 0.0004861 0.0019473 00:00:35.000 2022-09-16 20:14:24.000 <undefined> Pulse Regular
mask = segmentedData.Step_class == "Pulse";
pulseIndex = unique(segmentedData.Steps(mask));
pulseIndex = reshape(pulseIndex,2,[])';
pulseIndex = [pulseIndex,pulseIndex(:,2)+1];
disp(pulseIndex) 9 10 11
13 14 15
17 18 19
21 22 23
25 26 27
29 30 31
33 34 35
37 38 39
Extract features from pulses
The pulseIndex variable is an 8-by-3 array, with each row being the indices for a complete 3-step pulse segment (i.e., the step before a current pulse, a current pulse, and the step following a current pulse). For the identified pulses, the helper function hExtractPulseFeature computes the following features for each of the eight pulses in the RPT:
Slope_K1 =
Slope_K2 =
Slope_K3 =
Slope_K4 =
Mean_Pulse_Voltage =
mean(voltage across three segments)Var_Pulse_Voltage =
var(voltage across three segments)Kurtosis_Pulse_Voltage =
kurtosis(voltage across three segments)Relaxation_End_Voltage =
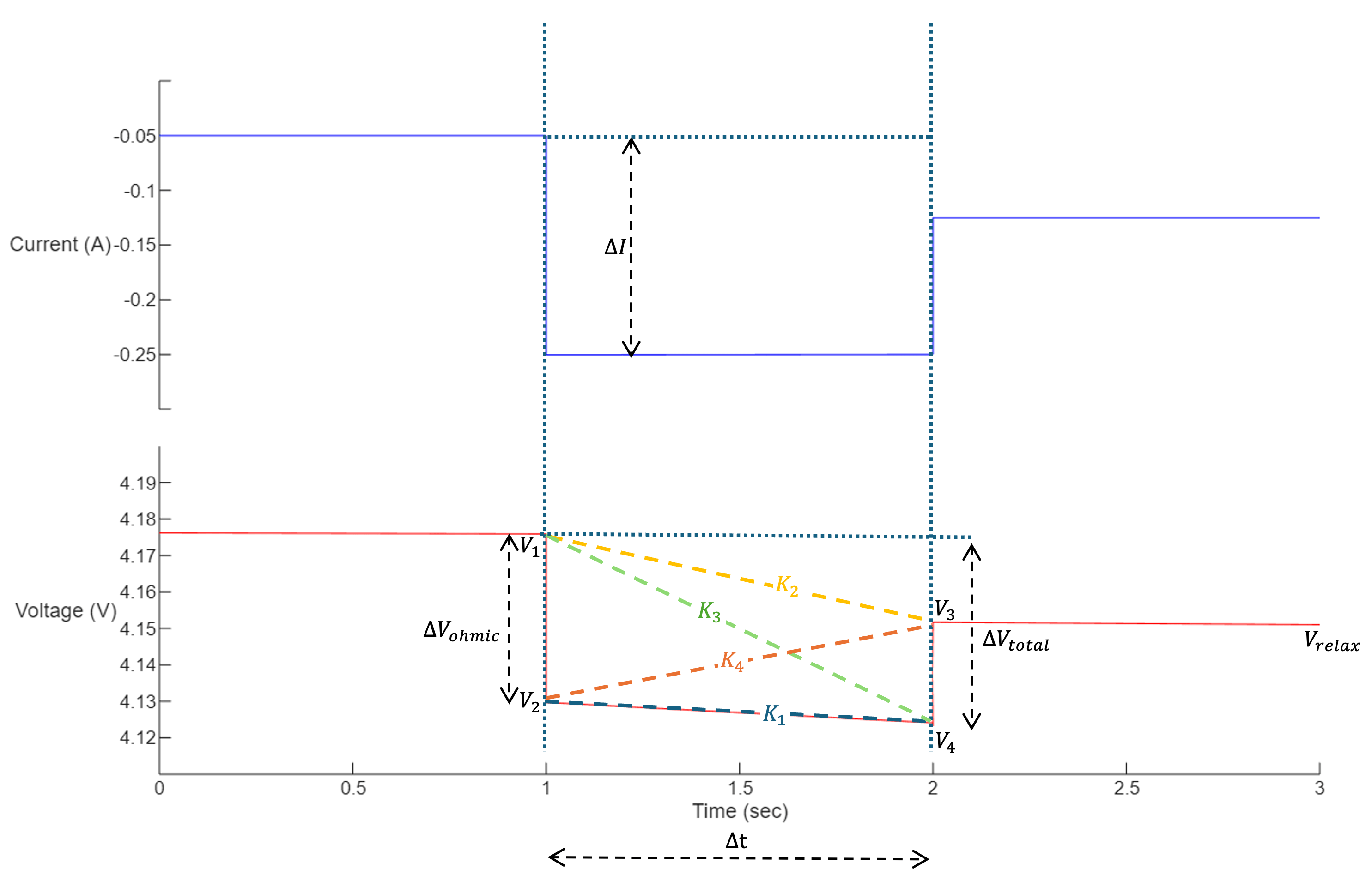
The suffix in the column name is the index of the pulse in a RPT from which the feature is extracted.
FeatureTable = hExtractPulseFeature(segmentedData,pulseIndex); head(FeatureTable)
R_ohmic_1 R_total_1 Slope_K1_1 Slope_K2_1 Slope_K3_1 Slope_K4_1 mean_Pulse_Voltage_1 var_Pulse_Voltage_1 kurtosis_Pulse_Voltage_1 Relaxation_End_Voltage_1 R_ohmic_2 R_total_2 Slope_K1_2 Slope_K2_2 Slope_K3_2 Slope_K4_2 mean_Pulse_Voltage_2 var_Pulse_Voltage_2 kurtosis_Pulse_Voltage_2 Relaxation_End_Voltage_2 R_ohmic_3 R_total_3 Slope_K1_3 Slope_K2_3 Slope_K3_3 Slope_K4_3 mean_Pulse_Voltage_3 var_Pulse_Voltage_3 kurtosis_Pulse_Voltage_3 Relaxation_End_Voltage_3 R_ohmic_4 R_total_4 Slope_K1_4 Slope_K2_4 Slope_K3_4 Slope_K4_4 mean_Pulse_Voltage_4 var_Pulse_Voltage_4 kurtosis_Pulse_Voltage_4 Relaxation_End_Voltage_4 R_ohmic_5 R_total_5 Slope_K1_5 Slope_K2_5 Slope_K3_5 Slope_K4_5 mean_Pulse_Voltage_5 var_Pulse_Voltage_5 kurtosis_Pulse_Voltage_5 Relaxation_End_Voltage_5 R_ohmic_6 R_total_6 Slope_K1_6 Slope_K2_6 Slope_K3_6 Slope_K4_6 mean_Pulse_Voltage_6 var_Pulse_Voltage_6 kurtosis_Pulse_Voltage_6 Relaxation_End_Voltage_6 R_ohmic_7 R_total_7 Slope_K1_7 Slope_K2_7 Slope_K3_7 Slope_K4_7 mean_Pulse_Voltage_7 var_Pulse_Voltage_7 kurtosis_Pulse_Voltage_7 Relaxation_End_Voltage_7 R_ohmic_8 R_total_8 Slope_K1_8 Slope_K2_8 Slope_K3_8 Slope_K4_8 mean_Pulse_Voltage_8 var_Pulse_Voltage_8 kurtosis_Pulse_Voltage_8 Relaxation_End_Voltage_8
_________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________ _________ _________ __________ __________ __________ __________ ____________________ ___________________ ________________________ ________________________
0.24 0.265 -0.005 -0.0245 -0.053 0.0235 4.0908 0.0037578 1.6321 4.0057 0.2325 0.2495 -Inf -Inf -Inf Inf 3.8893 0.0063696 1.7985 3.7605 0.229 0.2445 -0.0031 -0.0207 -0.0489 0.0251 3.6475 0.0063288 1.7698 3.5249 0.2415 0.2665 -0.005 -0.0217 -0.0533 0.0266 3.5189 0.00054497 1.6027 3.4867 0.23699 0.27449 -0.0075 -0.0233 -0.0549 0.0241 3.4813 0.00066076 1.6166 3.4433 0.25553 0.2995 -0.0087 -0.0267 -0.0599 0.0245 3.434 0.00093928 1.7297 3.3851 0.254 0.3485 -0.0189 -0.0363 -0.0697 0.0145 3.3 0.016161 2.4567 3.0468 0.19436 0.62348 -0.0859 -0.1076 -0.1247 -0.0688 3.1929 0.0028879 1.9654 3.2759
0.23057 0.2635 -0.0065 -0.0242 -0.0527 0.022 4.0889 0.0036989 1.6712 4.0048 0.197 0.245 -0.0096 -0.022 -0.049 0.0174 3.8906 0.0064627 1.7844 3.7568 0.21741 0.2415 -0.0049 -0.0204 -0.0483 0.023 3.6467 0.0063932 1.7642 3.5243 0.2385 0.262 -0.0047 -0.0217 -0.0524 0.026 3.5213 0.00049425 1.5017 3.4914 0.22091 0.26999 -0.0099 -0.0224 -0.054 0.0217 3.4833 0.00059733 1.5478 3.4489 0.2415 0.2915 -0.01 -0.026 -0.0583 0.0223 3.4335 0.00094114 1.7574 3.3835 0.19587 0.33199 -0.0273 -0.0351 -0.0664 0.004 3.3101 0.013146 2.54 3.0741 0.19719 0.569 -0.0744 -0.0837 -0.1138 -0.0443 3.1345 0.0023419 2.1134 3.2114
0.22104 0.265 -0.009 -0.0248 -0.053 0.0192 4.0893 0.0036391 1.6727 4.006 0.2265 0.24604 -0.004 -0.022 -0.0493 0.0233 3.8909 0.0064134 1.7892 3.7593 0.228 0.2435 -0.0031 -0.0207 -0.0487 0.0249 3.6458 0.00647 1.7671 3.5227 0.2435 0.265 -Inf -Inf -Inf Inf 3.5212 0.00050504 1.4996 3.4908 0.24649 0.27599 -Inf -Inf -Inf Inf 3.4847 0.00060268 1.4807 3.4489 0.24974 0.2945 -0.009 -0.0263 -0.0589 0.0236 3.4337 0.00092506 1.7462 3.3841 0.25553 0.3395 -0.0167 -0.0158 -0.0679 0.0354 3.3204 0.01092 2.5723 3.0974 0.25274 0.555 -0.0605 -0.0722 -0.111 -0.0217 3.1222 0.0020445 2.2562 3.1907
0.2125 0.2745 -0.0124 -0.0257 -0.0549 0.0168 4.0888 0.0035983 1.6819 4.0048 0.22259 0.256 -0.0066 -0.0226 -0.0512 0.022 3.8921 0.0064132 1.7777 3.7605 0.236 0.253 -0.0034 -0.0217 -0.0506 0.0255 3.6478 0.0064092 1.7662 3.5249 0.2445 0.2755 -0.0062 -0.0229 -0.0551 0.026 3.5207 0.00052895 1.5185 3.4908 0.24973 0.28499 -0.0071 -0.0239 -0.057 0.026 3.4812 0.00067423 1.6108 3.4433 0.2114 0.301 -0.018 -0.0059 -0.0602 0.0363 3.4352 0.00094892 1.7435 3.3835 0.22799 0.33949 -0.0223 -0.0351 -0.0679 0.0105 3.2877 0.018159 2.5163 3 0.2665 0.5315 -0.053 -0.0595 -0.1063 -0.0062 3.1035 0.0016413 2.7146 3.1637
0.24373 0.2805 -0.0074 -0.027 -0.0561 0.0217 4.0871 0.0036353 1.6994 4.0045 0.2295 0.256 -0.0053 -0.0229 -0.0512 0.023 3.8909 0.0065378 1.779 3.758 0.23644 0.25299 -0.0034 -0.0217 -0.0506 0.0255 3.6471 0.0065039 1.7659 3.5227 0.2495 0.277 -0.0055 -0.0232 -0.0554 0.0267 3.5207 0.00054115 1.5185 3.4905 0.2495 0.285 -0.0071 -0.0242 -0.057 0.0257 3.4814 0.00067806 1.6149 3.4433 0.24732 0.3025 -0.0109 -0.0273 -0.0605 0.0223 3.4373 0.0008658 1.6368 3.3916 0.22458 0.338 -0.0226 -0.0351 -0.0676 0.0099 3.2872 0.018019 2.4479 3.0028 0.22971 0.49598 -0.0533 -0.053 -0.0992 -0.0071 3.0904 0.0015444 2.7748 3.1473
0.2109 0.2805 -0.014 -0.0254 -0.0561 0.0167 4.0873 0.0036188 1.6864 4.0039 0.237 0.259 -0.0044 -0.0232 -0.0518 0.0242 3.8915 0.0064427 1.7854 3.7605 0.23645 0.2545 -0.0037 -0.0217 -0.0509 0.0255 3.6491 0.0064046 1.765 3.5255 0.2295 0.284 -0.0109 -0.0236 -0.0568 0.0223 3.5211 0.00054454 1.5286 3.4905 0.25549 0.28949 -0.0068 -0.0043 -0.0579 0.0468 3.4851 0.00062516 1.4825 3.4492 0.25403 0.307 -0.0105 -0.0279 -0.0614 0.023 3.4372 0.00090095 1.6394 3.3903 0.22843 0.34099 -0.0226 -0.0357 -0.0682 0.0099 3.288 0.017494 2.3888 3.0109 0.26949 0.48948 -0.044 -0.0536 -0.0979 0.0003 3.0831 0.0014663 2.7124 3.137
0.243 0.282 -0.0078 -0.0276 -0.0564 0.021 4.086 0.0036318 1.7108 4.0039 0.23655 0.25899 -0.0044 -0.0229 -0.0518 0.0245 3.8908 0.0065288 1.7864 3.7589 0.2129 0.25599 -0.0087 -0.0196 -0.0512 0.0229 3.649 0.0065362 1.75 3.5233 0.24823 0.28549 -0.0075 -0.0239 -0.0571 0.0257 3.5209 0.00055955 1.5215 3.4902 0.2555 0.2915 -0.0072 -0.0046 -0.0583 0.0465 3.485 0.00064314 1.4628 3.4492 0.25552 0.30999 -0.0108 -0.0282 -0.062 0.023 3.4369 0.0009327 1.6478 3.3888 0.245 0.3425 -0.0195 -0.0357 -0.0685 0.0133 3.2853 0.017821 2.3017 3.0109 0.2525 0.4695 -0.0434 -0.0431 -0.0939 0.0074 3.0758 0.0013801 2.859 3.1274
0.24023 0.282 -0.0084 -0.0279 -0.0564 0.0201 4.0856 0.0036491 1.7118 4.0035 0.234 0.256 -0.0044 -0.0037 -0.0512 0.0431 3.8915 0.0067584 1.7697 3.7568 0.23923 0.2545 -0.0031 -0.022 -0.0509 0.0258 3.6504 0.0063927 1.7609 3.5264 0.25474 0.287 -Inf -Inf -Inf Inf 3.522 0.00056946 1.4454 3.4898 0.23572 0.291 -0.0111 -0.0254 -0.0582 0.0217 3.4839 0.00064495 1.5475 3.4489 0.25749 0.31149 -0.0108 -0.009 -0.0623 0.0425 3.4383 0.00094386 1.6318 3.3875 0.225 0.3425 -0.0235 -0.0363 -0.0685 0.0087 3.2911 0.01751 2.4071 3.014 0.23122 0.457 -0.0452 -0.04 -0.0914 0.0062 3.0725 0.0013136 2.8724 3.1231
To estimate the health of the cell, use the helper function hFindCapacity to calculate the remaining capacity of the cell and capacity loss at each RPT.
[capacity,capacityLoss] = hFindCapacity(segmentedData); capacityTable = array2table([capacity,capacityLoss],... 'VariableNames',["Remaining_Capacity","Capacity_Loss"]); head(capacityTable)
Remaining_Capacity Capacity_Loss
__________________ _____________
0.28524 0
0.28411 0.0011261
0.28285 0.0023864
0.27962 0.0056198
0.27672 0.00852
0.27418 0.011059
0.27213 0.013109
0.27008 0.015162
Plot the extracted features to visualize any trends that indicate correlation with aging.
rptFeaturesToPlot = ["mean_Pulse_Voltage_3","R_ohmic_8"]; for iii = 1:length(rptFeaturesToPlot) figure() yyaxis left plot(FeatureTable,rptFeaturesToPlot(iii)) xlabel('RPT Index') ylabel(rptFeaturesToPlot(iii),Interpreter="none") yyaxis right plot(capacityTable,"Capacity_Loss") ylabel('Capacity loss(Ah)') end
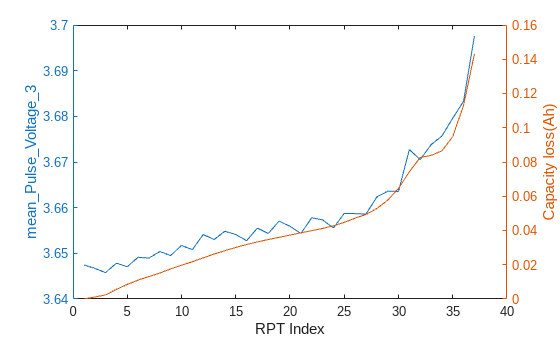
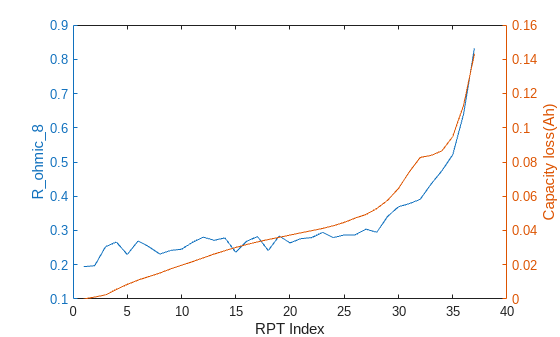
The trends of these features as cell ages align with the capacity loss, but the evolution of feature values is not smooth as the capacity loss. The main reason is that the current pulse in this dataset is only applied for 1 seconds, which is a very short period of time so that cell is still in transient state. This will result in higher noise in the feature extraction because the measurements can be taken at different stage of the transient state.
Conclusion
This example illustrates automatic segmentation of pulses from battery reference performance tests using deep learning. Automatic data segmentation reduces the need for manual intermediate data processing to extract pulse or other type of test components (e.g., EIS). Synthetic data simulated from physics-based models could be used to expand the capability of such deep learning models for more complicated RPT designs, such as a blend of charge and discharge pulses.
The segmented data was used to extract key features that show strong correlation with the capacity loss as the cell ages. These features can then be used as predictors of state of health or other battery health indicators.
[1] Thelen, Adam; Li, Tingkai; Liu, Jinqiang; Tischer, Chad; Hu, Chao (2023). ISU-ILCC Battery Aging Dataset. Iowa State University. Dataset. https://doi.org/10.25380/iastate.22582234.v2
See Also
Topics
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: United States.
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)